新人教版高中数学选择性必修第三册7.1~7.3综合拔高练
文档属性
| 名称 | 新人教版高中数学选择性必修第三册7.1~7.3综合拔高练 |  | |
| 格式 | docx | ||
| 文件大小 | 123.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 14:30:52 | ||
图片预览




文档简介
7.1~7.3综合拔高练
五年高考练
考点 离散型随机变量的均值与方差
1.(2020课标全国Ⅲ理,3,5分,)在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且pi=1,则下面四种情形中,对应样本的标准差最大的一组是( )
A.p1=p4=0.1,p2=p3=0.4 B.p1=p4=0.4,p2=p3=0.1
C.p1=p4=0.2,p2=p3=0.3 D.p1=p4=0.3,p2=p3=0.2
2.(2019北京,17,13分,)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付金额(元)支付方式 (0,1 000] (1 000,2 000] 大于2 000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(2)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1 000元的人数,求X的分布列和数学期望;
(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2 000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2 000元的人数有变化 说明理由.
3.(2019课标全国Ⅰ,21,12分,)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈,则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈,则乙药得1分,甲药得-1分;若都治愈或都未治愈,则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
(i)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
(ii)求p4,并根据p4的值解释这种试验方案的合理性.
三年模拟练
应用实践
1.(2020福建福州一中高二下适应性考试,)从1,2,3,4,5中任取2个不同的数,事件A表示“取到的2个数之和为偶数”,事件B表示“取到的两个数均为偶数”,则P(B|A)=( )
A. B.
C. D.
2.(2020重庆巴蜀中学高二下月考,)已知A学校有15位数学老师,其中9位男老师,6位女老师,B学校有10位数学老师,其中3位男老师,7位女老师,为了实现师资均衡,现从A学校任意抽取一位数学老师到B学校,然后从B学校随机抽取一位数学老师到市里上公开课,则两次都抽到男老师的概率是( )
A. B.
C. D.
3.(2020山东淄博桓台一中高二下期中,)已知随机变量X的分布列如下:
X -1 0 1
P
且Y=aX+3,E(Y)=,则a= .
4.(2020河北邯郸第一中学高二期中,)设验血诊断某种疾病的误诊率为5%,即若用A表示验血为阳性,B表示受验者患病,则P(|B)=P(A|)=0.05.若受检人群中有0.5%患此病,即P(B)=0.005,则一个验血为阳性的人确患此病的概率为 .
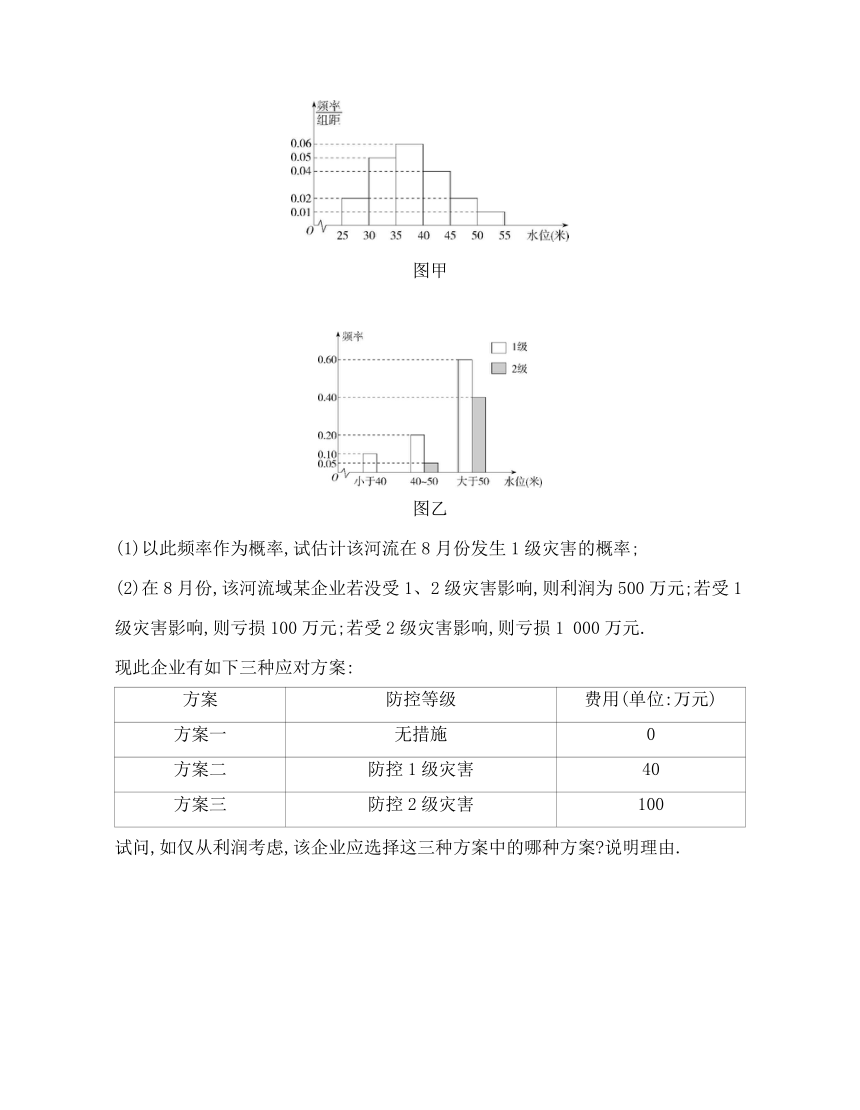
5.(2020河北沧州一中高二下月考,)依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图甲所示;依据当地的地质构造,得到水位与灾害等级的条形图如图乙所示.
图甲
图乙
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)在8月份,该河流域某企业若没受1、2级灾害影响,则利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响,则亏损1 000万元.
现此企业有如下三种应对方案:
方案 防控等级 费用(单位:万元)
方案一 无措施 0
方案二 防控1级灾害 40
方案三 防控2级灾害 100
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案 说明理由.
6.(2020山东济宁一中高三下质量检测,)某班级体育课进行一次定点投篮测试,规定每人最多投3次,每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用X表示,如果X的值不低于3就判定为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.现有两种投篮方案:方案1,先在A处投一球,以后都在B处投;方案2,都在B处投篮.已知甲同学在A处投篮的命中率为,在B处投篮的命中率为.
(1)若甲同学选择方案1,求他测试结束后所得总分X的分布列和数学期望;
(2)你认为甲同学选择哪种方案通过测试的可能性更大 说明理由.
迁移创新
7.(2020江西瑞金四校高三第三次联考,)2020年新冠肺炎给世界人民带来了巨大的灾难,面对新冠肺炎,早发现、早报告、早隔离、早诊断、早治疗是有效防控疾病蔓延的重要举措之一.某社区对55位居民是否患有新冠肺炎进行筛查,先到社区医务室进行咽拭子核酸检测,检测结果呈阳性者,再到医院做进一步检查,已知这55位居民随机一人其咽拭子核酸检测结果呈阳性的概率为2%,且每个人的咽拭子核酸检测是否呈阳性相互独立.
(1)假设患新冠肺炎的概率是0.3%,且患病者咽拭子核酸检测呈阳性的概率为98%,设这55位居民中有一位的咽拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
(2)假设咽拭子核酸检测采用分组检测法可有效减少工作量,具体操作如下:将55位居民分成若干组,先取每组居民的咽拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
方案一:将55位居民分成11组,每组5人;
方案二:将55位居民分成5组,每组11人.
试分析哪一个方案的工作量更少.
(参考数据:0.985≈0.904,0.9811≈0.801)
答案全解全析
7.1~7.3综合拔高练
五年高考练
1.B 根据均值E(X)=xipi,方差D(X)=[xi-E(X)]2pi以及方差与标准差的关系,得各选项对应样本的标准差如下表.
选项 均值E(X) 方差D(X) 标准差
A 2.5 0.65
B 2.5 1.85
C 2.5 1.05
D 2.5 1.45
由此可知选项B对应样本的标准差最大,故选B.
2.解析 (1)由题意知,样本中仅使用A的学生有18+9+3=30人,仅使用B的学生有10+14+1=25人,A,B两种支付方式都不使用的学生有5人.
故样本中A,B两种支付方式都使用的学生有100-30-25-5=40人.
所以从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率为=0.4.
(2)X的可能取值为0,1,2.
记事件C为“从样本仅使用A的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”,事件D为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”.
由题设知,事件C,D相互独立,且P(C)==0.4,P(D)==0.6.
所以P(X=2)=P(CD)=P(C)P(D)=0.24,
P(X=1)=P(C∪D)
=P(C)P()+P()P(D)
=0.4×(1-0.6)+(1-0.4)×0.6=0.52,
P(X=0)=P()=P()P()=0.24.
所以X的分布列为
X 0 1 2
P 0.24 0.52 0.24
故X的数学期望E(X)=0×0.24+1×0.52+2×0.24=1.
(3)记事件E为“从样本仅使用A的学生中随机抽查3人,他们本月的支付金额都大于2 000元”.
假设样本仅使用A的学生中,本月支付金额大于2 000元的人数没有变化,
则由上个月的样本数据得P(E)==.
答案示例1:可以认为有变化.
理由如下:
P(E)比较小,概率比较小的事件一般不容易发生.一旦发生,就有理由认为本月的支付金额大于2 000元的人数发生了变化,所以可以认为有变化.
答案示例2:无法确定有没有变化.
理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
3.解析 (1)X的可能取值为-1,0,1.
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β).
所以X的分布列为
X -1 0 1
P (1-α)β αβ+(1-α)(1-β) α(1-β)
(2)(i)证明:由(1)得a=0.4,b=0.5,c=0.1.
因此pi=0.4pi-1+0.5pi+0.1pi+1,
故0.1(pi+1-pi)=0.4(pi-pi-1),
即pi+1-pi=4(pi-pi-1).
又因为p1-p0=p1≠0,
所以{pi+1-pi}(i=0,1,2,…,7)是公比为4,首项为p1的等比数列.
(ii)由(i)可得p8=p8-p7+p7-p6+…+p1-p0+p0=(p8-p7)+(p7-p6)+…+(p1-p0)=p1.
由于p8=1,故p1=,
所以p4=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)=p1=.
p4表示最终认为甲药更有效的概率.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为p4=≈0.003 9,此时得出错误结论的概率非常小,说明这种试验方案合理.
三年模拟练
1.B 依题意P(A)===,P(AB)==,故P(B|A)===.故选B.
2.B 设“从A学校抽取的数学老师是男老师”为事件M,“从B学校抽取的数学老师是男老师”为事件N,
则由题意可知P(M)==,
P(N|M)==,
则两次都抽到男老师的概率P(MN)=P(M)P(N|M)=×=.
故选B.
3.答案 4
解析 ∵E(X)=-1×+0×+1×=-,Y=aX+3,
∴E(Y)=aE(X)+3=,
即-a+3=,解得a=4.
4.答案
解析 P(B|A)
=
==.
5.解析 (1)依据题图甲,记该河流8月份“水位小于40米”为事件A1,“水位在40米至50米之间”为事件A2,“水位大于50米”为事件A3,
则P(A1)=(0.02+0.05+0.06)×5=0.65,
P(A2)=(0.04+0.02)×5=0.30,
P(A3)=0.01×5=0.05.
记该地8月份“水位小于40米且发生1级灾害”为事件B1,“水位在40米至50米之间且发生1级灾害”为事件B2,“水位大于50米且发生1级灾害”为事件B3,
则P(B1)=0.10,P(B2)=0.20,P(B3)=0.60.
记“该河流在8月份发生1级灾害”为事件B,则P(B)=P(A1B1)+P(A2B2)+P(A3B3)=P(A1)P(B1)+P(A2)P(B2)+P(A3)P(B3)
=0.65×0.10+0.30×0.20+0.05×0.60=0.155.
故估计该河流在8月份发生1级灾害的概率为0.155.
(2)以企业利润为随机变量,
若选择方案一,则利润X1的可能取值为500,-100,-1 000,由(1)知
P(X1=500)=0.65×0.90+0.30×0.75+0.05×0=0.81,
P(X1=-100)=0.155,
P(X1=-1 000)=0.65×0+0.30×0.05+0.05×0.40=0.035.
故X1的分布列为
X1 500 -100 -1 000
P 0.81 0.155 0.035
则该企业在8月份的利润期望E(X1)=500×0.81+(-100)×0.155+(-1 000)×0.035=354.5.
若选择方案二,则利润X2的可能取值为460,-1 040,由(1)知,
P(X2=460)=0.81+0.155=0.965,
P(X2=-1 040)=0.035.
故X2的分布列为
X2 460 -1 040
P 0.965 0.035
则该企业在8月份的利润期望E(X2)=460×0.965+(-1 040)×0.035=407.5.
若选择方案三,则该企业在8月份的利润期望E(X3)=500-100=400.
因为E(X2)>E(X3)>E(X1),所以该企业应选择方案二.
6.解析 (1)设甲同学在A处投中为事件A,在B处第i次投中为事件Bi(i=1,2),
则P(A)=,P(Bi)=.
X的可能取值为0,2,3,4,
P(X=0)=P()=P()P()·P()=××=,
P(X=2)=P(B1)+P(B2)=××+××=,
P(X=3)=P(A)=,
P(X=4)=P(B1B2)=××=,
故X的分布列为
X 0 2 3 4
P
X的数学期望E(X)=0×+2×+3×+4×==3.15.
(2)设甲同学选择方案1通过测试的概率为P1,选择方案2通过测试的概率为P2,
则由(1)得P1=P(X=3)+P(X=4)=+==0.73,
P2=×+××+××
==0.896,
∵P2>P1,
∴甲同学选择方案2通过测试的可能性更大.
7.解析 (1)设事件A为 “咽拭子核酸检测呈阳性”,事件B为“患新冠肺炎”.
由题意可得P(A)=0.02,P(B)=0.003,
P(A|B)=0.98,
由概率的乘法公式,
得P(AB)=P(B)P(A|B)=0.003×0.98,
所以P(B|A)===0.147.
故咽拭子核酸检测呈阳性的居民可以确诊为新冠肺炎患者的概率为14.7%.
(2)设方案一中每组的检测次数为X,则X的可能取值为1,6,
P(X=1)=(1-0.02)5=0.985≈0.904,
P(X=6)=1-0.985≈0.096,
所以X的分布列为
X 1 6
P 0.904 0.096
所以E(X)=1×0.904+6×0.096=1.48,
即方案一检测的总次数的期望为11×1.48=16.28.
设方案二中每组的检测次数为Y,则Y的可能取值为1,12,
P(Y=1)=(1-0.02)11=0.9811≈0.801,
P(Y=12)=1-0.9811≈0.199,
所以Y的分布列为
Y 1 12
P 0.801 0.199
所以E(Y)=1×0.801+12×0.199=3.189.
即方案二检测的总次数的期望为5×3.189=15.945.
因为16.28>15.945,所以方案二的工作量更少.
五年高考练
考点 离散型随机变量的均值与方差
1.(2020课标全国Ⅲ理,3,5分,)在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且pi=1,则下面四种情形中,对应样本的标准差最大的一组是( )
A.p1=p4=0.1,p2=p3=0.4 B.p1=p4=0.4,p2=p3=0.1
C.p1=p4=0.2,p2=p3=0.3 D.p1=p4=0.3,p2=p3=0.2
2.(2019北京,17,13分,)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付金额(元)支付方式 (0,1 000] (1 000,2 000] 大于2 000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(2)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1 000元的人数,求X的分布列和数学期望;
(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2 000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2 000元的人数有变化 说明理由.
3.(2019课标全国Ⅰ,21,12分,)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈,则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈,则乙药得1分,甲药得-1分;若都治愈或都未治愈,则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
(i)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
(ii)求p4,并根据p4的值解释这种试验方案的合理性.
三年模拟练
应用实践
1.(2020福建福州一中高二下适应性考试,)从1,2,3,4,5中任取2个不同的数,事件A表示“取到的2个数之和为偶数”,事件B表示“取到的两个数均为偶数”,则P(B|A)=( )
A. B.
C. D.
2.(2020重庆巴蜀中学高二下月考,)已知A学校有15位数学老师,其中9位男老师,6位女老师,B学校有10位数学老师,其中3位男老师,7位女老师,为了实现师资均衡,现从A学校任意抽取一位数学老师到B学校,然后从B学校随机抽取一位数学老师到市里上公开课,则两次都抽到男老师的概率是( )
A. B.
C. D.
3.(2020山东淄博桓台一中高二下期中,)已知随机变量X的分布列如下:
X -1 0 1
P
且Y=aX+3,E(Y)=,则a= .
4.(2020河北邯郸第一中学高二期中,)设验血诊断某种疾病的误诊率为5%,即若用A表示验血为阳性,B表示受验者患病,则P(|B)=P(A|)=0.05.若受检人群中有0.5%患此病,即P(B)=0.005,则一个验血为阳性的人确患此病的概率为 .
5.(2020河北沧州一中高二下月考,)依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图甲所示;依据当地的地质构造,得到水位与灾害等级的条形图如图乙所示.
图甲
图乙
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)在8月份,该河流域某企业若没受1、2级灾害影响,则利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响,则亏损1 000万元.
现此企业有如下三种应对方案:
方案 防控等级 费用(单位:万元)
方案一 无措施 0
方案二 防控1级灾害 40
方案三 防控2级灾害 100
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案 说明理由.
6.(2020山东济宁一中高三下质量检测,)某班级体育课进行一次定点投篮测试,规定每人最多投3次,每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用X表示,如果X的值不低于3就判定为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.现有两种投篮方案:方案1,先在A处投一球,以后都在B处投;方案2,都在B处投篮.已知甲同学在A处投篮的命中率为,在B处投篮的命中率为.
(1)若甲同学选择方案1,求他测试结束后所得总分X的分布列和数学期望;
(2)你认为甲同学选择哪种方案通过测试的可能性更大 说明理由.
迁移创新
7.(2020江西瑞金四校高三第三次联考,)2020年新冠肺炎给世界人民带来了巨大的灾难,面对新冠肺炎,早发现、早报告、早隔离、早诊断、早治疗是有效防控疾病蔓延的重要举措之一.某社区对55位居民是否患有新冠肺炎进行筛查,先到社区医务室进行咽拭子核酸检测,检测结果呈阳性者,再到医院做进一步检查,已知这55位居民随机一人其咽拭子核酸检测结果呈阳性的概率为2%,且每个人的咽拭子核酸检测是否呈阳性相互独立.
(1)假设患新冠肺炎的概率是0.3%,且患病者咽拭子核酸检测呈阳性的概率为98%,设这55位居民中有一位的咽拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
(2)假设咽拭子核酸检测采用分组检测法可有效减少工作量,具体操作如下:将55位居民分成若干组,先取每组居民的咽拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
方案一:将55位居民分成11组,每组5人;
方案二:将55位居民分成5组,每组11人.
试分析哪一个方案的工作量更少.
(参考数据:0.985≈0.904,0.9811≈0.801)
答案全解全析
7.1~7.3综合拔高练
五年高考练
1.B 根据均值E(X)=xipi,方差D(X)=[xi-E(X)]2pi以及方差与标准差的关系,得各选项对应样本的标准差如下表.
选项 均值E(X) 方差D(X) 标准差
A 2.5 0.65
B 2.5 1.85
C 2.5 1.05
D 2.5 1.45
由此可知选项B对应样本的标准差最大,故选B.
2.解析 (1)由题意知,样本中仅使用A的学生有18+9+3=30人,仅使用B的学生有10+14+1=25人,A,B两种支付方式都不使用的学生有5人.
故样本中A,B两种支付方式都使用的学生有100-30-25-5=40人.
所以从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率为=0.4.
(2)X的可能取值为0,1,2.
记事件C为“从样本仅使用A的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”,事件D为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”.
由题设知,事件C,D相互独立,且P(C)==0.4,P(D)==0.6.
所以P(X=2)=P(CD)=P(C)P(D)=0.24,
P(X=1)=P(C∪D)
=P(C)P()+P()P(D)
=0.4×(1-0.6)+(1-0.4)×0.6=0.52,
P(X=0)=P()=P()P()=0.24.
所以X的分布列为
X 0 1 2
P 0.24 0.52 0.24
故X的数学期望E(X)=0×0.24+1×0.52+2×0.24=1.
(3)记事件E为“从样本仅使用A的学生中随机抽查3人,他们本月的支付金额都大于2 000元”.
假设样本仅使用A的学生中,本月支付金额大于2 000元的人数没有变化,
则由上个月的样本数据得P(E)==.
答案示例1:可以认为有变化.
理由如下:
P(E)比较小,概率比较小的事件一般不容易发生.一旦发生,就有理由认为本月的支付金额大于2 000元的人数发生了变化,所以可以认为有变化.
答案示例2:无法确定有没有变化.
理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
3.解析 (1)X的可能取值为-1,0,1.
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β).
所以X的分布列为
X -1 0 1
P (1-α)β αβ+(1-α)(1-β) α(1-β)
(2)(i)证明:由(1)得a=0.4,b=0.5,c=0.1.
因此pi=0.4pi-1+0.5pi+0.1pi+1,
故0.1(pi+1-pi)=0.4(pi-pi-1),
即pi+1-pi=4(pi-pi-1).
又因为p1-p0=p1≠0,
所以{pi+1-pi}(i=0,1,2,…,7)是公比为4,首项为p1的等比数列.
(ii)由(i)可得p8=p8-p7+p7-p6+…+p1-p0+p0=(p8-p7)+(p7-p6)+…+(p1-p0)=p1.
由于p8=1,故p1=,
所以p4=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)=p1=.
p4表示最终认为甲药更有效的概率.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为p4=≈0.003 9,此时得出错误结论的概率非常小,说明这种试验方案合理.
三年模拟练
1.B 依题意P(A)===,P(AB)==,故P(B|A)===.故选B.
2.B 设“从A学校抽取的数学老师是男老师”为事件M,“从B学校抽取的数学老师是男老师”为事件N,
则由题意可知P(M)==,
P(N|M)==,
则两次都抽到男老师的概率P(MN)=P(M)P(N|M)=×=.
故选B.
3.答案 4
解析 ∵E(X)=-1×+0×+1×=-,Y=aX+3,
∴E(Y)=aE(X)+3=,
即-a+3=,解得a=4.
4.答案
解析 P(B|A)
=
==.
5.解析 (1)依据题图甲,记该河流8月份“水位小于40米”为事件A1,“水位在40米至50米之间”为事件A2,“水位大于50米”为事件A3,
则P(A1)=(0.02+0.05+0.06)×5=0.65,
P(A2)=(0.04+0.02)×5=0.30,
P(A3)=0.01×5=0.05.
记该地8月份“水位小于40米且发生1级灾害”为事件B1,“水位在40米至50米之间且发生1级灾害”为事件B2,“水位大于50米且发生1级灾害”为事件B3,
则P(B1)=0.10,P(B2)=0.20,P(B3)=0.60.
记“该河流在8月份发生1级灾害”为事件B,则P(B)=P(A1B1)+P(A2B2)+P(A3B3)=P(A1)P(B1)+P(A2)P(B2)+P(A3)P(B3)
=0.65×0.10+0.30×0.20+0.05×0.60=0.155.
故估计该河流在8月份发生1级灾害的概率为0.155.
(2)以企业利润为随机变量,
若选择方案一,则利润X1的可能取值为500,-100,-1 000,由(1)知
P(X1=500)=0.65×0.90+0.30×0.75+0.05×0=0.81,
P(X1=-100)=0.155,
P(X1=-1 000)=0.65×0+0.30×0.05+0.05×0.40=0.035.
故X1的分布列为
X1 500 -100 -1 000
P 0.81 0.155 0.035
则该企业在8月份的利润期望E(X1)=500×0.81+(-100)×0.155+(-1 000)×0.035=354.5.
若选择方案二,则利润X2的可能取值为460,-1 040,由(1)知,
P(X2=460)=0.81+0.155=0.965,
P(X2=-1 040)=0.035.
故X2的分布列为
X2 460 -1 040
P 0.965 0.035
则该企业在8月份的利润期望E(X2)=460×0.965+(-1 040)×0.035=407.5.
若选择方案三,则该企业在8月份的利润期望E(X3)=500-100=400.
因为E(X2)>E(X3)>E(X1),所以该企业应选择方案二.
6.解析 (1)设甲同学在A处投中为事件A,在B处第i次投中为事件Bi(i=1,2),
则P(A)=,P(Bi)=.
X的可能取值为0,2,3,4,
P(X=0)=P()=P()P()·P()=××=,
P(X=2)=P(B1)+P(B2)=××+××=,
P(X=3)=P(A)=,
P(X=4)=P(B1B2)=××=,
故X的分布列为
X 0 2 3 4
P
X的数学期望E(X)=0×+2×+3×+4×==3.15.
(2)设甲同学选择方案1通过测试的概率为P1,选择方案2通过测试的概率为P2,
则由(1)得P1=P(X=3)+P(X=4)=+==0.73,
P2=×+××+××
==0.896,
∵P2>P1,
∴甲同学选择方案2通过测试的可能性更大.
7.解析 (1)设事件A为 “咽拭子核酸检测呈阳性”,事件B为“患新冠肺炎”.
由题意可得P(A)=0.02,P(B)=0.003,
P(A|B)=0.98,
由概率的乘法公式,
得P(AB)=P(B)P(A|B)=0.003×0.98,
所以P(B|A)===0.147.
故咽拭子核酸检测呈阳性的居民可以确诊为新冠肺炎患者的概率为14.7%.
(2)设方案一中每组的检测次数为X,则X的可能取值为1,6,
P(X=1)=(1-0.02)5=0.985≈0.904,
P(X=6)=1-0.985≈0.096,
所以X的分布列为
X 1 6
P 0.904 0.096
所以E(X)=1×0.904+6×0.096=1.48,
即方案一检测的总次数的期望为11×1.48=16.28.
设方案二中每组的检测次数为Y,则Y的可能取值为1,12,
P(Y=1)=(1-0.02)11=0.9811≈0.801,
P(Y=12)=1-0.9811≈0.199,
所以Y的分布列为
Y 1 12
P 0.801 0.199
所以E(Y)=1×0.801+12×0.199=3.189.
即方案二检测的总次数的期望为5×3.189=15.945.
因为16.28>15.945,所以方案二的工作量更少.
