8.4.2 空间点、直线、平面之间的位置关系 教案(表格式)
文档属性
| 名称 | 8.4.2 空间点、直线、平面之间的位置关系 教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 360.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 11:01:33 | ||
图片预览


文档简介
8.4.2 空间点、直线、平面之间的位置关系
【教材分析】
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第八章《立体几何初步》,本节课主要学习空间点、直线、平面之间的位置关系。
教材从观察长方体中点、直线、平面之间的位置关系以及上一节所学点与直线、直线与平面的位置关系开始,认识空间中点、直线、平面之间的位置关系,通过大量图形、实验、和说理,使学生进一步了解点、直线、平面之间的位置关系。
学习空间点、直线、平面之间的位置关系为下一步学习判断直线与平面的平行、垂直打基础。
【教学目标】
课程目标 学科素养
A.了解空间中两条直线的三种位置关系,理解两异面直线的定义,会用平面衬托来画异面直线; B.了解直线与平面的三种位置关系,并会用图形语言和符号语言表示; C.了解不重合的两个平面之间的两种位置关系,并会用图形语言和符号语言表示. 1.数学抽象:点、直线、平面之间的位置关系; 2.逻辑推理:直线与平面的位置关系、平面与平面的位置关系; 3.直观想象:两条直线的三种位置关系。
【重点与难点】
1.教学重点:两条直线的三种位置关系,异面直线的定义,直线与平面的三种位置关系,两个平面之间的两种位置关系;
2.教学难点:异面直线的定义,两个平面之间的两种位置关系,并会用图形语言和符号语言表示。
【教学准备】
多媒体
【教学过程】
教学过程 教学设计意图 核心素养目标
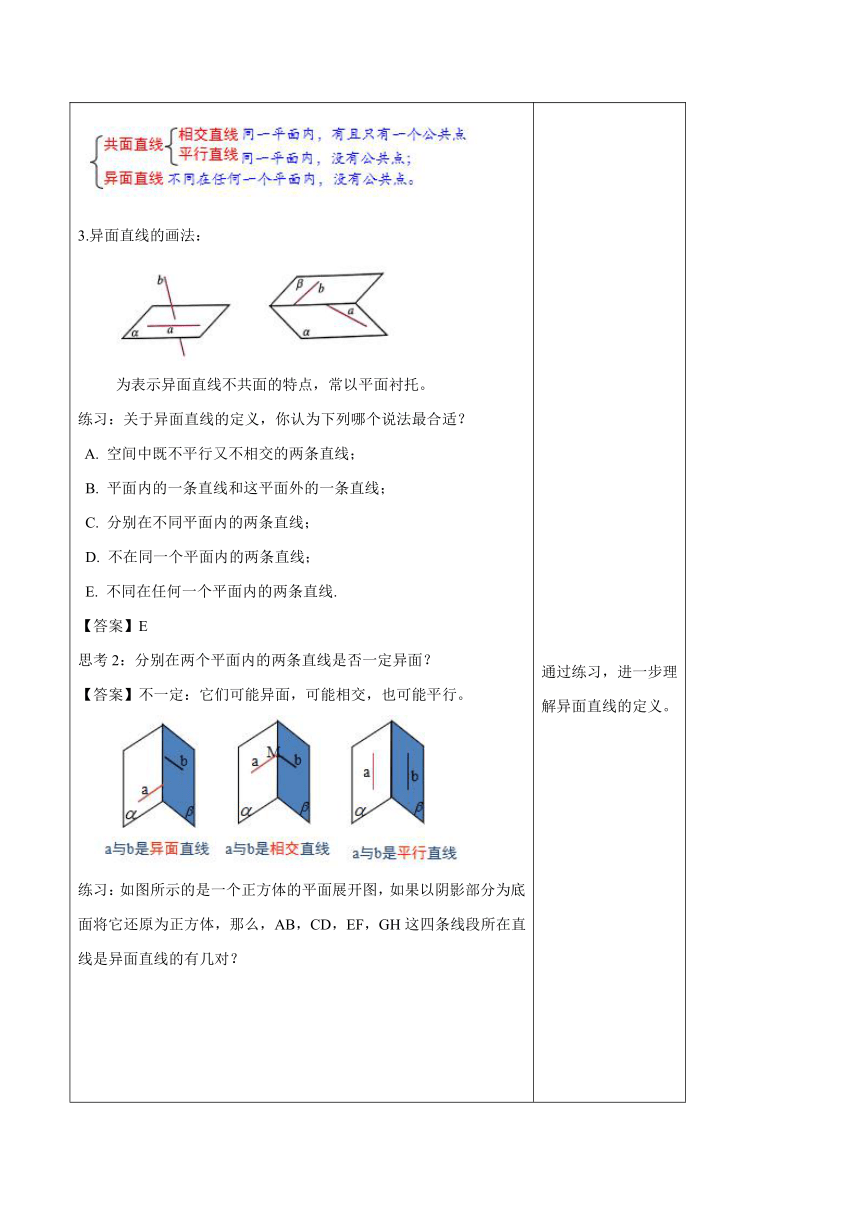
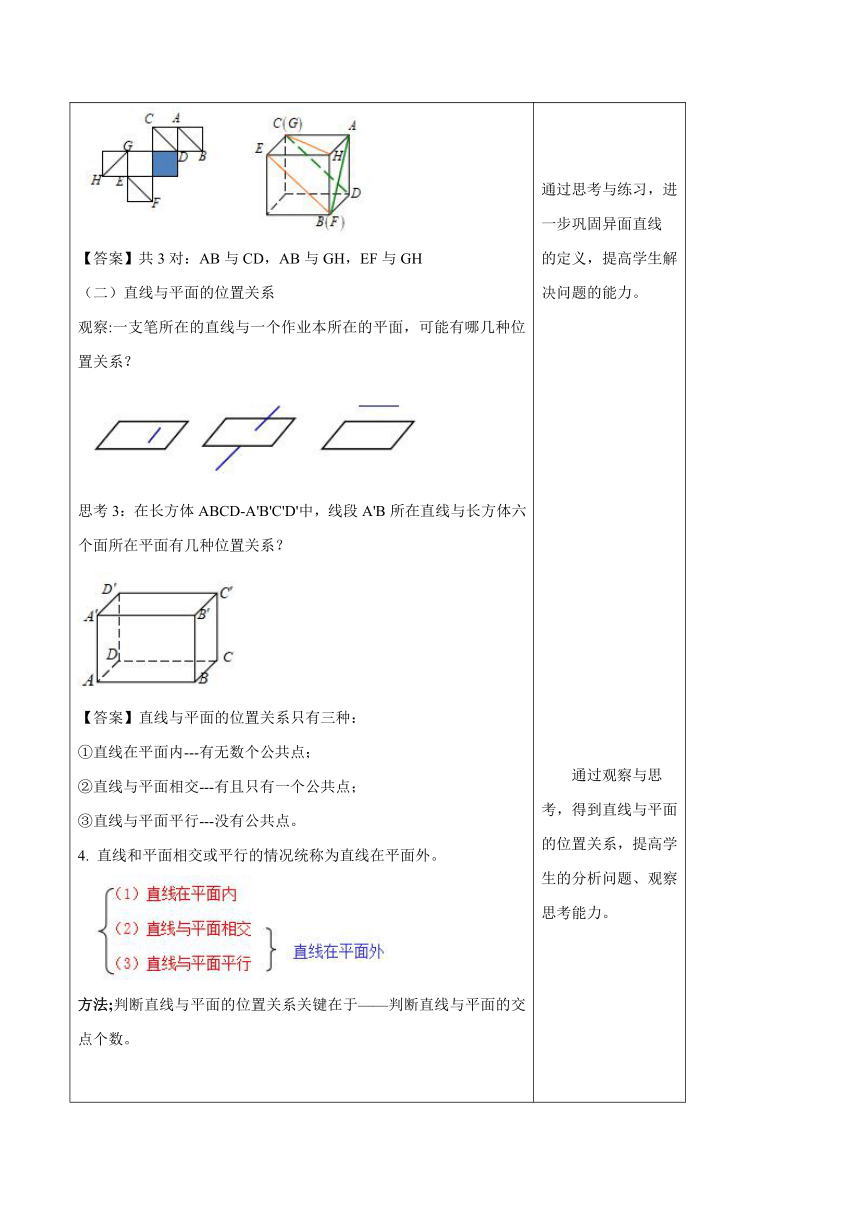
复习回顾,温故知新 1.点与直线的位置关系是什么?用数学符号怎样表示? 【答案】点在直线上,点不在直线上 2.直线与平面的位置关系是什么?用数学符号怎样表示? 【答案】点在平面内,点不在平面内 二、探索新知 思考1:我们知道,长方体有8个顶点,12条棱,6个面,12条棱对应12条棱所在的直线,6个面对应6个面所在的平面,如图所示的长方体,你能发现这些顶点、直线、平面之间的位置关系吗? 【分析】 , (一)两直线的位置关系 观察1:黑板两侧所在的直线与课桌边沿所在直线是什么位置关系? 观察2:旗杆所在的直线与其正后方跑道所在直线是什么位置关系? 1.定义:不同在任何一个平面内的两条直线叫做异面直线(skew lines) 2.空间两条直线的位置关系: 3.异面直线的画法: 为表示异面直线不共面的特点,常以平面衬托。 练习:关于异面直线的定义,你认为下列哪个说法最合适? A. 空间中既不平行又不相交的两条直线; B. 平面内的一条直线和这平面外的一条直线; C. 分别在不同平面内的两条直线; D. 不在同一个平面内的两条直线; E. 不同在任何一个平面内的两条直线. 【答案】E 思考2:分别在两个平面内的两条直线是否一定异面? 【答案】不一定:它们可能异面,可能相交,也可能平行。 练习:如图所示的是一个正方体的平面展开图,如果以阴影部分为底面将它还原为正方体,那么,AB,CD,EF,GH这四条线段所在直线是异面直线的有几对? 【答案】共3对:AB与CD,AB与GH,EF与GH (二)直线与平面的位置关系 观察:一支笔所在的直线与一个作业本所在的平面,可能有哪几种位置关系? 思考3:在长方体ABCD-A'B'C'D'中,线段A'B所在直线与长方体六个面所在平面有几种位置关系? 【答案】直线与平面的位置关系只有三种: ①直线在平面内---有无数个公共点; ②直线与平面相交---有且只有一个公共点; ③直线与平面平行---没有公共点。 4. 直线和平面相交或平行的情况统称为直线在平面外。 方法;判断直线与平面的位置关系关键在于——判断直线与平面的交点个数。 图形表示: 符号表示: (三)平面与平面之间的位置关系 观察1:如图,围成长方体ABCD-A′B′C′D′的六个面,两两之间 的位置关系有几种? 观察2:教室里的地面与桌面、黑板面所在墙面与地面之间有哪些关系? 【答案】桌面与地面平行,墙面与地面:相交。 6.两个平面的位置关系只有两种:即两个平面平行,两个平面相交. (1)两个平面平行---没有公共点; (2)两个平面相交---有一条公共直线. 图形表示: 符号表示: 注意:画两个互相平行平面时,要注意使表示平面的两个平行四边形的对应边平行。 探究:如图,在长方体中,连接, 请你再举出一些图中表示空间直线、平面之间位置关系的例子, 并用符号表示这些位置关系。 【答案】, 例1.如图,用符号表示下列图形中直线、平面之间的位置关系。 解:在(1)中, 在(1)中, 例2.如图 直线AB与直线a具有怎样的位置关系?为什么? 解:直线AB与a是异面直线。理由如下。 若直线AB与直线a不是异面直线,则它们相交或平行。 设它们确定的平面为,则 。由于经过点B与直线a有且仅有一个平面,因此平面与平面重合,从而,进而,这与矛盾。 所以直线AB与a是异面直线。 方法总结:判断两直线是异面直线的方法: 与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。 通过复习上节所学知识,引入本节新课。建立知识间的联系,提高学生概括、类比推理的能力。 通过思考,观察图形,引入新课,提高学生分析问题的能力。 通过观察实际生活中的例子,引入异面直线,提高学生分析问题、概括能力。 通过练习,进一步理解异面直线的定义。 通过思考与练习,进一步巩固异面直线的定义,提高学生解决问题的能力。 通过观察与思考,得到直线与平面的位置关系,提高学生的分析问题、观察思考能力。 通过方法总结,提高学生的概括能力、解决问题的能力。 通过观察,得到平面与平面的位置关系,提高学生的分析问题、观察思考能力。 通过探究,进一步熟悉直线、平面之间的位置关系,提高学生解决问题的能力。 通过例题的讲解,让学生进一步理解直线、平面之间的位置关系及其符号表示,提高学生解决与分析问题的能力。
三、达标检测 1.判断正误 (1)在空间中,直线不平行就意味着相交.( ) (2)直线在平面外是指直线与平面没有交点.( ) (3)两个平面相交的时候,一定交于一条直线.( ) 【答案】 (1)× (2)× (3)√ 2.圆柱的两个底面的位置关系是( ) A.相交 B.平行 C.平行或异面 D.相交或异面 【答案】B 【解析】圆柱的两个底面无公共点,则它们平行. 3.下列命题: ①两个平面有无数个公共点,则这两个平面重合; ②若l,m是异面直线,l∥α,m∥β,则α∥β. 其中错误命题的序号为 . 【答案】①② 【解析】①中两个平面也可能相交;②α与β可能平行也可能相交. 4.如图,在正方体ABCD A1B1C1D1中,分别指出直线B1C,D1B与正方体六个面所在平面的关系. 【解析】 根据图形,直线B1C 平面B1C,直线B1C∥平面A1D,与其余四个面相交,直线D1B与正方体六个面均相交. 通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
四、小结 1. 两条直线的位置关系; 2.直线与平面的位置关系; 3.平面与平面的位置关系。 五、作业 习题8.4 4,9题 通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
【教学反思】
判断空间点、直线、平面之间的位置关系应多借助于模型,让学生多观察,发现它们之间的位置关系,多找模型,让学生自己动手去找模型,思考判断。
【教材分析】
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第八章《立体几何初步》,本节课主要学习空间点、直线、平面之间的位置关系。
教材从观察长方体中点、直线、平面之间的位置关系以及上一节所学点与直线、直线与平面的位置关系开始,认识空间中点、直线、平面之间的位置关系,通过大量图形、实验、和说理,使学生进一步了解点、直线、平面之间的位置关系。
学习空间点、直线、平面之间的位置关系为下一步学习判断直线与平面的平行、垂直打基础。
【教学目标】
课程目标 学科素养
A.了解空间中两条直线的三种位置关系,理解两异面直线的定义,会用平面衬托来画异面直线; B.了解直线与平面的三种位置关系,并会用图形语言和符号语言表示; C.了解不重合的两个平面之间的两种位置关系,并会用图形语言和符号语言表示. 1.数学抽象:点、直线、平面之间的位置关系; 2.逻辑推理:直线与平面的位置关系、平面与平面的位置关系; 3.直观想象:两条直线的三种位置关系。
【重点与难点】
1.教学重点:两条直线的三种位置关系,异面直线的定义,直线与平面的三种位置关系,两个平面之间的两种位置关系;
2.教学难点:异面直线的定义,两个平面之间的两种位置关系,并会用图形语言和符号语言表示。
【教学准备】
多媒体
【教学过程】
教学过程 教学设计意图 核心素养目标
复习回顾,温故知新 1.点与直线的位置关系是什么?用数学符号怎样表示? 【答案】点在直线上,点不在直线上 2.直线与平面的位置关系是什么?用数学符号怎样表示? 【答案】点在平面内,点不在平面内 二、探索新知 思考1:我们知道,长方体有8个顶点,12条棱,6个面,12条棱对应12条棱所在的直线,6个面对应6个面所在的平面,如图所示的长方体,你能发现这些顶点、直线、平面之间的位置关系吗? 【分析】 , (一)两直线的位置关系 观察1:黑板两侧所在的直线与课桌边沿所在直线是什么位置关系? 观察2:旗杆所在的直线与其正后方跑道所在直线是什么位置关系? 1.定义:不同在任何一个平面内的两条直线叫做异面直线(skew lines) 2.空间两条直线的位置关系: 3.异面直线的画法: 为表示异面直线不共面的特点,常以平面衬托。 练习:关于异面直线的定义,你认为下列哪个说法最合适? A. 空间中既不平行又不相交的两条直线; B. 平面内的一条直线和这平面外的一条直线; C. 分别在不同平面内的两条直线; D. 不在同一个平面内的两条直线; E. 不同在任何一个平面内的两条直线. 【答案】E 思考2:分别在两个平面内的两条直线是否一定异面? 【答案】不一定:它们可能异面,可能相交,也可能平行。 练习:如图所示的是一个正方体的平面展开图,如果以阴影部分为底面将它还原为正方体,那么,AB,CD,EF,GH这四条线段所在直线是异面直线的有几对? 【答案】共3对:AB与CD,AB与GH,EF与GH (二)直线与平面的位置关系 观察:一支笔所在的直线与一个作业本所在的平面,可能有哪几种位置关系? 思考3:在长方体ABCD-A'B'C'D'中,线段A'B所在直线与长方体六个面所在平面有几种位置关系? 【答案】直线与平面的位置关系只有三种: ①直线在平面内---有无数个公共点; ②直线与平面相交---有且只有一个公共点; ③直线与平面平行---没有公共点。 4. 直线和平面相交或平行的情况统称为直线在平面外。 方法;判断直线与平面的位置关系关键在于——判断直线与平面的交点个数。 图形表示: 符号表示: (三)平面与平面之间的位置关系 观察1:如图,围成长方体ABCD-A′B′C′D′的六个面,两两之间 的位置关系有几种? 观察2:教室里的地面与桌面、黑板面所在墙面与地面之间有哪些关系? 【答案】桌面与地面平行,墙面与地面:相交。 6.两个平面的位置关系只有两种:即两个平面平行,两个平面相交. (1)两个平面平行---没有公共点; (2)两个平面相交---有一条公共直线. 图形表示: 符号表示: 注意:画两个互相平行平面时,要注意使表示平面的两个平行四边形的对应边平行。 探究:如图,在长方体中,连接, 请你再举出一些图中表示空间直线、平面之间位置关系的例子, 并用符号表示这些位置关系。 【答案】, 例1.如图,用符号表示下列图形中直线、平面之间的位置关系。 解:在(1)中, 在(1)中, 例2.如图 直线AB与直线a具有怎样的位置关系?为什么? 解:直线AB与a是异面直线。理由如下。 若直线AB与直线a不是异面直线,则它们相交或平行。 设它们确定的平面为,则 。由于经过点B与直线a有且仅有一个平面,因此平面与平面重合,从而,进而,这与矛盾。 所以直线AB与a是异面直线。 方法总结:判断两直线是异面直线的方法: 与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。 通过复习上节所学知识,引入本节新课。建立知识间的联系,提高学生概括、类比推理的能力。 通过思考,观察图形,引入新课,提高学生分析问题的能力。 通过观察实际生活中的例子,引入异面直线,提高学生分析问题、概括能力。 通过练习,进一步理解异面直线的定义。 通过思考与练习,进一步巩固异面直线的定义,提高学生解决问题的能力。 通过观察与思考,得到直线与平面的位置关系,提高学生的分析问题、观察思考能力。 通过方法总结,提高学生的概括能力、解决问题的能力。 通过观察,得到平面与平面的位置关系,提高学生的分析问题、观察思考能力。 通过探究,进一步熟悉直线、平面之间的位置关系,提高学生解决问题的能力。 通过例题的讲解,让学生进一步理解直线、平面之间的位置关系及其符号表示,提高学生解决与分析问题的能力。
三、达标检测 1.判断正误 (1)在空间中,直线不平行就意味着相交.( ) (2)直线在平面外是指直线与平面没有交点.( ) (3)两个平面相交的时候,一定交于一条直线.( ) 【答案】 (1)× (2)× (3)√ 2.圆柱的两个底面的位置关系是( ) A.相交 B.平行 C.平行或异面 D.相交或异面 【答案】B 【解析】圆柱的两个底面无公共点,则它们平行. 3.下列命题: ①两个平面有无数个公共点,则这两个平面重合; ②若l,m是异面直线,l∥α,m∥β,则α∥β. 其中错误命题的序号为 . 【答案】①② 【解析】①中两个平面也可能相交;②α与β可能平行也可能相交. 4.如图,在正方体ABCD A1B1C1D1中,分别指出直线B1C,D1B与正方体六个面所在平面的关系. 【解析】 根据图形,直线B1C 平面B1C,直线B1C∥平面A1D,与其余四个面相交,直线D1B与正方体六个面均相交. 通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
四、小结 1. 两条直线的位置关系; 2.直线与平面的位置关系; 3.平面与平面的位置关系。 五、作业 习题8.4 4,9题 通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
【教学反思】
判断空间点、直线、平面之间的位置关系应多借助于模型,让学生多观察,发现它们之间的位置关系,多找模型,让学生自己动手去找模型,思考判断。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
