5.1.2导数的概念及其几何意义 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册(共17张PPT)
文档属性
| 名称 | 5.1.2导数的概念及其几何意义 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 14:40:34 | ||
图片预览






文档简介
(共17张PPT)
5.1.2导数的概念及其几何意义
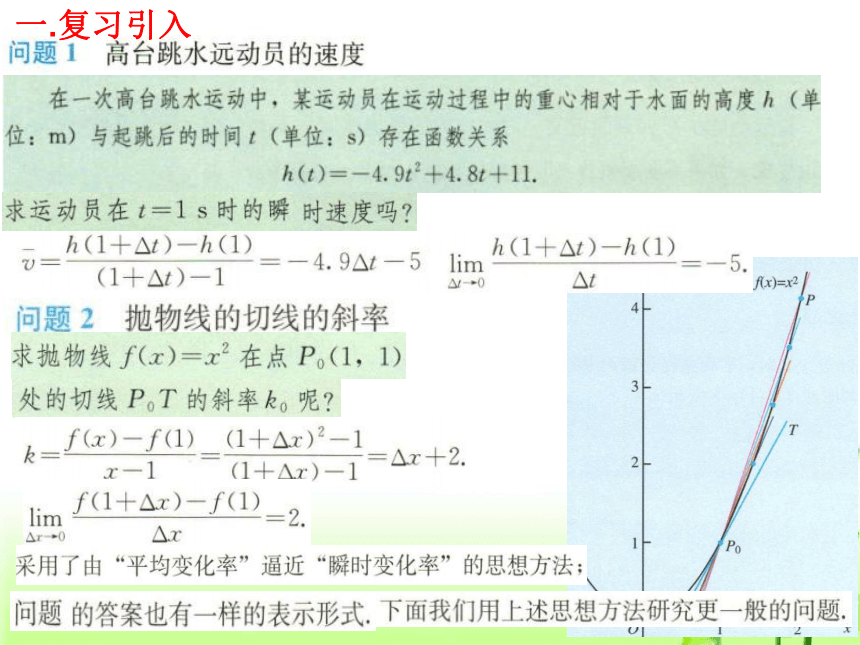
一.复习引入
1.平均变化率
注意:
步骤:
二.讲授新课
0
练习1
2.1
2.导数(瞬时变化率)
思考1:
例如:
求导数的步骤?
练习2
三.例题讲解
练习3
C
B
3.切线定义
思考2. 割线P0P 的斜率与切线P0T斜率
的有什么关系?
1.
4.导数的几何意义
5.y=f(x)的导函数
步骤:
4.求函数y=f(x)=x2的导函数?
小结
1.平均变化率
2.导数(瞬时变化率)
3.切线定义
4.导数的几何意义
5.y=f(x)的导函数
fx)=x2
4
P
3
T
2
1
Po
0
2
x
思考
观察函数y=f(x)的图象(图5.1-3),平
y=f(x)/
均变化率
fxo+△x)
P
△yf(xo+△x)-f(xo)
△x
△x
fxo+△x)-fxo)
f(xo)
Po
表示什么?瞬时变化率
△x
Xo
xo+△x
f,)=一是-四
f(xo十△x)-f(xo)
△x+0
△x
图5.1-3
表示什么?
y个
y=fx)
f(xo)
Po
0
XO
文
1.5
0.5
B
++++H+++++++++H+++++++1+HH+H++◆+++++H+H+++++++过+H++
o.5千fx)=sin(X)
A
-1.5
继续观察图5.1-4,可以发现点P。处的切线P。T比任
何一条割线更贴近点P。附近的曲线.进一步地,利用信息
技术工具将点P。附近的曲线不断放大(图5.1-5),可以发
现点P。附近的曲线越来越接近于直线.因此,在点P。附
近,曲线y=f(x)可以用点P。处的切线P。T近似代替.①
解:我们用曲线h(t)在t=to,t1,t2处的切线斜率,刻画曲线h(t)在上述三个时
刻附近的变化情况.
(1)当t=to时,曲线h(t)在t=to处的切线lo平行于t轴,h'(to)=0.这时,在t=
t。附近曲线比较平坦,几乎没有升降.
(2)当t=t1时,曲线h(t)在t=t1处的切线l1的斜率h'(t1)<0.这时,在t=t1
附近曲线下降,即函数h(t)在t=t1附近单调递减,
(3)当t=t2时,曲线h(t)在t=t2处的切线l2的斜率h'(t2)<0.这时,在t=t2
附近曲线下降,即函数h(t)在t=t2附近也单调递减.
从图5.1-6可以看出,直线1的倾斜程度小于直线l2的倾斜程度,这说明曲线h(t)
在t=t1附近比在t=t2附近下降得缓慢.
5.1.2导数的概念及其几何意义
一.复习引入
1.平均变化率
注意:
步骤:
二.讲授新课
0
练习1
2.1
2.导数(瞬时变化率)
思考1:
例如:
求导数的步骤?
练习2
三.例题讲解
练习3
C
B
3.切线定义
思考2. 割线P0P 的斜率与切线P0T斜率
的有什么关系?
1.
4.导数的几何意义
5.y=f(x)的导函数
步骤:
4.求函数y=f(x)=x2的导函数?
小结
1.平均变化率
2.导数(瞬时变化率)
3.切线定义
4.导数的几何意义
5.y=f(x)的导函数
fx)=x2
4
P
3
T
2
1
Po
0
2
x
思考
观察函数y=f(x)的图象(图5.1-3),平
y=f(x)/
均变化率
fxo+△x)
P
△yf(xo+△x)-f(xo)
△x
△x
fxo+△x)-fxo)
f(xo)
Po
表示什么?瞬时变化率
△x
Xo
xo+△x
f,)=一是-四
f(xo十△x)-f(xo)
△x+0
△x
图5.1-3
表示什么?
y个
y=fx)
f(xo)
Po
0
XO
文
1.5
0.5
B
++++H+++++++++H+++++++1+HH+H++◆+++++H+H+++++++过+H++
o.5千fx)=sin(X)
A
-1.5
继续观察图5.1-4,可以发现点P。处的切线P。T比任
何一条割线更贴近点P。附近的曲线.进一步地,利用信息
技术工具将点P。附近的曲线不断放大(图5.1-5),可以发
现点P。附近的曲线越来越接近于直线.因此,在点P。附
近,曲线y=f(x)可以用点P。处的切线P。T近似代替.①
解:我们用曲线h(t)在t=to,t1,t2处的切线斜率,刻画曲线h(t)在上述三个时
刻附近的变化情况.
(1)当t=to时,曲线h(t)在t=to处的切线lo平行于t轴,h'(to)=0.这时,在t=
t。附近曲线比较平坦,几乎没有升降.
(2)当t=t1时,曲线h(t)在t=t1处的切线l1的斜率h'(t1)<0.这时,在t=t1
附近曲线下降,即函数h(t)在t=t1附近单调递减,
(3)当t=t2时,曲线h(t)在t=t2处的切线l2的斜率h'(t2)<0.这时,在t=t2
附近曲线下降,即函数h(t)在t=t2附近也单调递减.
从图5.1-6可以看出,直线1的倾斜程度小于直线l2的倾斜程度,这说明曲线h(t)
在t=t1附近比在t=t2附近下降得缓慢.
