8.2.2一元线性回归模型参数的最小二乘估计(第1课时)课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第三册(共17张PPT)
文档属性
| 名称 | 8.2.2一元线性回归模型参数的最小二乘估计(第1课时)课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第三册(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
8.2.2一元线性回归模型参数的最小二乘估计第1课时
1.一元线性回归模型
因变量
响应变量
自变量
解释
a
b
随机误差
复习回顾
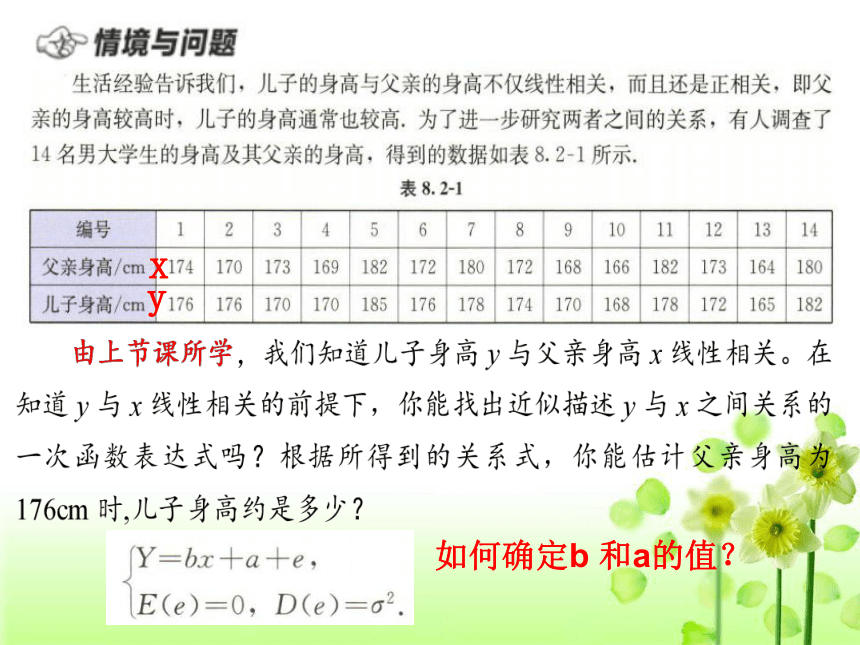
x
y
如何确定b 和a的值?
经验回归直线
1.经验回归方程
样本中心点
直线经过样本中心点
2.残差
观测值
预测值
残差
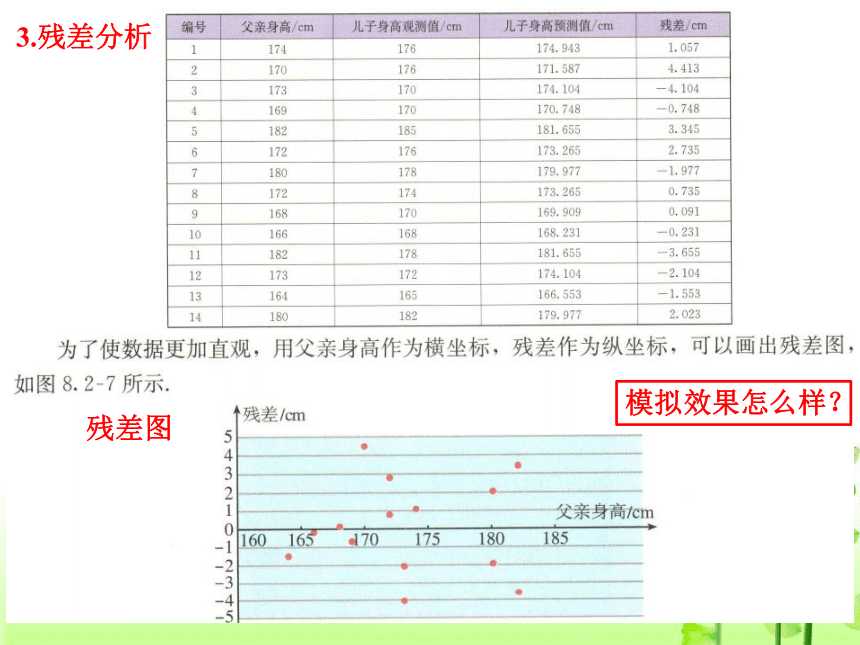
3.残差分析
残差图
模拟效果怎么样?
4.残差与随机误差的区别和联系
联系:都是衡量不确定性的指标.
随机误差是实际值与未知的总体回归线之间的纵向距离,反映除自变量外其他微小因素对因变量的影响,是不可测量的。
残差是实际值与样本回归线之间的纵向距离,当根据样本观测值拟合出样本回归线之后,可计算残差的具体数值。
区别:
利用残差可以对随机误差项进行估计。
练习1
2.
方法2:
4.
经验回归直线
1.经验回归方程
样本中心点
直线经过样本中心点
小结
2.残差
3.残差分析(残差图)
4.残差与随机误差的区别和联系
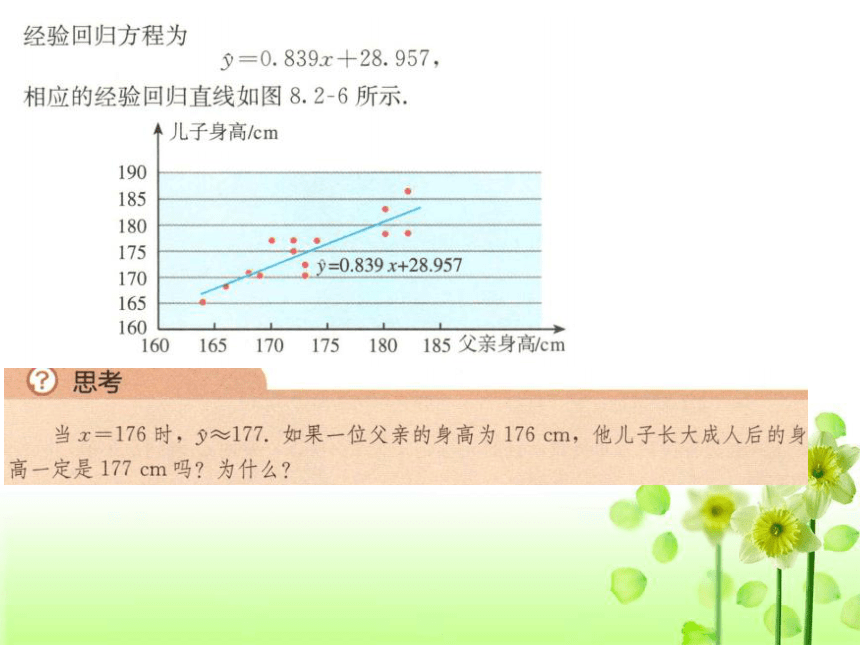
经验回归方程为
=0.839x+28.957,
相应的经验回归直线如图8.2-6所示
A儿子身高/cm
190
185
180
175
170
·=0.839x+28.957
165
160
160
165
170
175
180
185父亲身高/cm
编号
父亲身高/cm
儿子身高观测值/cm
儿子身高预测值/cm
残差/cm
1
174
176
174.943
1.057
2
170
176
171.587
4.413
3
173
170
174.104
-4.104
4
169
170
170.748
-0.748
5
182
185
181.655
3.345
6
172
176
173.265
2.735
7
180
178
179.977
-1.977
8
172
174
173.265
0.735
9
168
170
169.909
0.091
10
166
168
168.231
-0.231
11
182
178
181.655
-3.655
12
173
172
174.104
-2.104
13
164
165
166.553
-1.553
14
180
182
179.977
2.023
为了使数据更加直观,用父亲身高作为横坐标,残差作为纵坐标,可以画出残差图
如图8.2-7所示.
个残差/cm
54321012343
父亲身高cm
160
16570
175
180
185
8.2.2一元线性回归模型参数的最小二乘估计第1课时
1.一元线性回归模型
因变量
响应变量
自变量
解释
a
b
随机误差
复习回顾
x
y
如何确定b 和a的值?
经验回归直线
1.经验回归方程
样本中心点
直线经过样本中心点
2.残差
观测值
预测值
残差
3.残差分析
残差图
模拟效果怎么样?
4.残差与随机误差的区别和联系
联系:都是衡量不确定性的指标.
随机误差是实际值与未知的总体回归线之间的纵向距离,反映除自变量外其他微小因素对因变量的影响,是不可测量的。
残差是实际值与样本回归线之间的纵向距离,当根据样本观测值拟合出样本回归线之后,可计算残差的具体数值。
区别:
利用残差可以对随机误差项进行估计。
练习1
2.
方法2:
4.
经验回归直线
1.经验回归方程
样本中心点
直线经过样本中心点
小结
2.残差
3.残差分析(残差图)
4.残差与随机误差的区别和联系
经验回归方程为
=0.839x+28.957,
相应的经验回归直线如图8.2-6所示
A儿子身高/cm
190
185
180
175
170
·=0.839x+28.957
165
160
160
165
170
175
180
185父亲身高/cm
编号
父亲身高/cm
儿子身高观测值/cm
儿子身高预测值/cm
残差/cm
1
174
176
174.943
1.057
2
170
176
171.587
4.413
3
173
170
174.104
-4.104
4
169
170
170.748
-0.748
5
182
185
181.655
3.345
6
172
176
173.265
2.735
7
180
178
179.977
-1.977
8
172
174
173.265
0.735
9
168
170
169.909
0.091
10
166
168
168.231
-0.231
11
182
178
181.655
-3.655
12
173
172
174.104
-2.104
13
164
165
166.553
-1.553
14
180
182
179.977
2.023
为了使数据更加直观,用父亲身高作为横坐标,残差作为纵坐标,可以画出残差图
如图8.2-7所示.
个残差/cm
54321012343
父亲身高cm
160
16570
175
180
185
