新人教版八年级数学上册实数全章导学案(无答案)
文档属性
| 名称 | 新人教版八年级数学上册实数全章导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 64.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-09 00:00:00 | ||
图片预览




文档简介
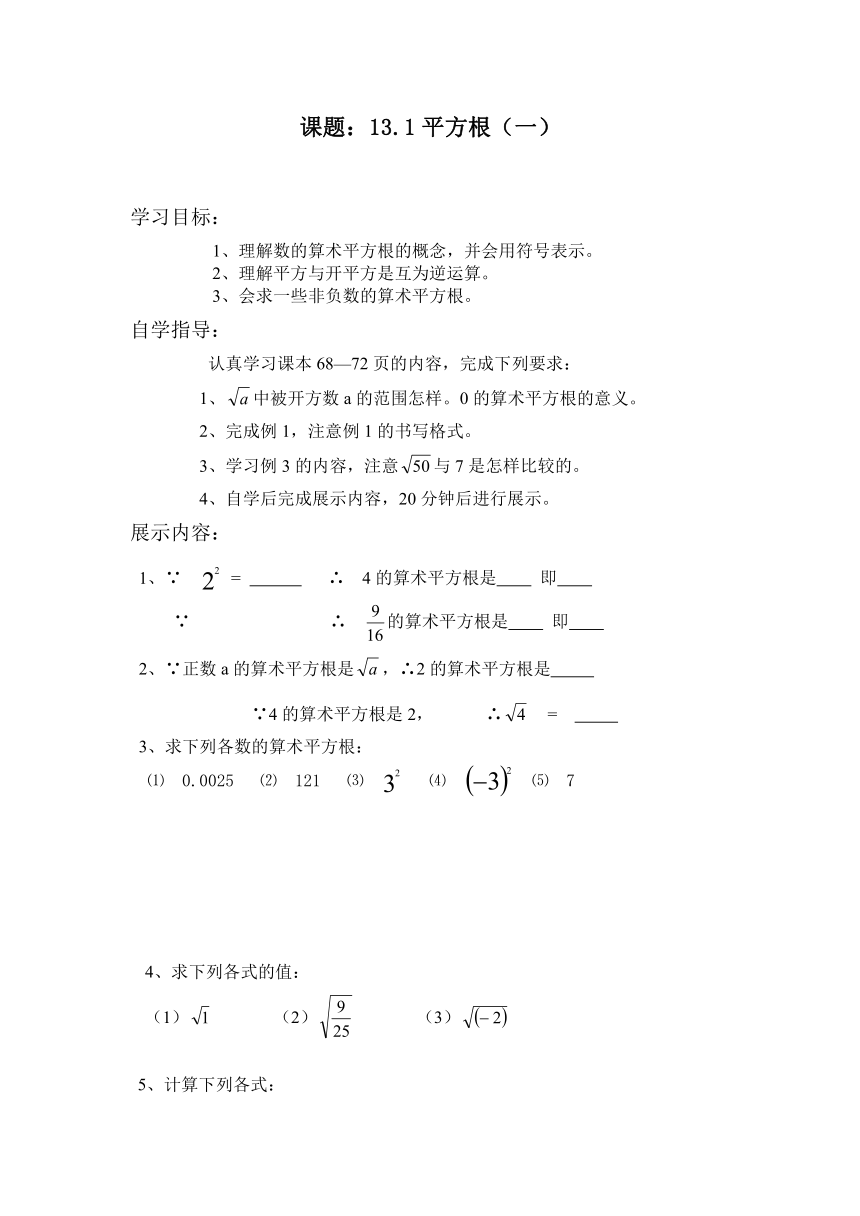
课题:13.1平方根(一)
学习目标:
理解数的算术平方根的概念,并会用符号表示。
理解平方与开平方是互为逆运算。
会求一些非负数的算术平方根。
自学指导:
认真学习课本68—72页的内容,完成下列要求:
1、中被开方数a的范围怎样。0的算术平方根的意义。
2、完成例1,注意例1的书写格式。
3、学习例3的内容,注意与7是怎样比较的。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、∵ = ∴ 4的算术平方根是 即
∵ ∴ 的算术平方根是 即
2、∵正数a的算术平方根是,∴2的算术平方根是
∵4的算术平方根是2, ∴ =
3、求下列各数的算术平方根:
⑴ 0.0025 ⑵ 121 ⑶ ⑷ ⑸ 7
4、求下列各式的值:
(1) (2) (3)
5、计算下列各式:
(1) — (2) — +
(3)×—×
6、求下列各等式中的正数x
(1) = 169 (2) 4 — 121 = 0
7、比较下列各组数的大小。
(1)与12 (2)与0.5
课后反思:
课题: 13.1平方根(二)
学习目标
理解平方根的概念
了解开平方的定义
掌握平方根的性质
自学指导
认真阅读72-74页内容,完成下列要求:
说明:一个正数a的算术平方根有__个,平方根有__个,并且互为____,0的平方根是___。
负数有没有平方根,为什么?
注意根号前的符号
自学20分钟后,进行展示活动
展示内容
填表:
X
8
-8
-
121
0.36
0
计算下列各式的值
(1) (2)- (3)± (4)-
平方根起源于正方形的面积,若一个正方形的面积为A,那么这个正方形的边长为多少?
判断下列说法是否正确
(1)5是25的算术平方根( )
(2)是的一个平方根( )
(3)的平方根是-4( )
(4)0的平方根与算术平方根都是0( )
5、下列各式是否有意义,为什么?
-(2)(3)(4)
6、求下列各式的x的值
(1)=25 (2)-81=0
(3)25=36 (4)2-18=0
课后反思:
课题:13.2 立方根
学习目标:
1、理解并掌握立方根的概念,会用符号表示一个数的立方根。
2、会求一个数的立方根。
自学指导:
自学课本77—78页内容,完成下列要求:
1、理解立方根的概念,理解立方与开立方是互为逆运算。
2、独立完成77页探究内容,组内合作交流,归纳出正数、负数、0的立方根的特点。
3、理解与—的相等关系。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、如果一个数的立方根等于 ,那么这个数叫做
的 或 。
2、求一个数的 的运算,叫做 。 与
互为逆运算。
3、正数的立方根是 数,负数的立方根是 数,0的立方根是 。
4、符号中,3是 ,中的 不能省略。
5、 —
6、课本79页练习1、3、4题
7、求下列各数的立方根。
(1)—8 (2) (3) ±125 (4) 81×9
8、求下列各式的值。
(1)— (2)— (3) (4)
(5)—
课后反思:
课题:13.3 实数(一)
学习目标
了解有理数、无理数、实数的概念及其分类
理解实数与数轴上的点是一一对应的关系
自学指导
认真阅读82页-84页的内容,完成下列要求:
举例说明什么是有限小数、无限小数、无限循球小数,无限不循环小数
、—、、都是无理数,那么带根号的数都是无理数吗?呢?
探究中直径为1的圆的周长是_,点O’的坐标是__
提示:举例说明什么是一一对应
展示内容
把下列各数分别填入相应的集合中
3.1415926 -8 0.6 0
有理数集合 无理数集合
正数集合 负数集合
请将数轴上的各点与下列实数对应起来
-1.5 3
-2 A 0 B C DE
3、选择,如图数轴上点A表示的是实数a,则点a到原点的距离是( )
a 0
A、a B、-a C、±a D、-|a|
4、下列说法正确的有( )个
(1)无限小数都是无理数
(2)无理数都是无限小数
(3)带根号的数都是无理数
(4)所有的有理数都可以用数轴上的点表示,反过来,数轴上的点都表示有理数
(5)所有的实数都要以用数轴上的点表示,反过来,数轴上的所有点都表示实数
A、1 B、2 C、3 D、4
5、有没有最小的正整数?有没有最小的整数?有没有最小的有理数?有没有最小的无理数?有没有最小的实数?有没有绝对值最小的实数?
课后反思:
课题:13.3 实数(二)
课型:预习展示 主备人:何立泉 审核人:何立泉 时间:
了解实数的运算法则及运算律,会进行实数的运算
明确有理数与实数的对比
自学指导
自学课本84-96页内容
回顾复习有理数的绝对值
小组交流课本84后思考题,归纳实数的相反数和绝对值的结果
明白有理数的运算法则及运算性质在进行实数的运算中,同样适用
展示内容
写出下列各数的相反数
(1)- (2) -3.14 (3)一
2、||=___ 若|a|=,则a=___
3、计算下列各式的值
(1)(+)- (2)3+2
(3)(-)-2(-)
课本86页1、2、3、4
课后反思:
学习目标:
理解数的算术平方根的概念,并会用符号表示。
理解平方与开平方是互为逆运算。
会求一些非负数的算术平方根。
自学指导:
认真学习课本68—72页的内容,完成下列要求:
1、中被开方数a的范围怎样。0的算术平方根的意义。
2、完成例1,注意例1的书写格式。
3、学习例3的内容,注意与7是怎样比较的。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、∵ = ∴ 4的算术平方根是 即
∵ ∴ 的算术平方根是 即
2、∵正数a的算术平方根是,∴2的算术平方根是
∵4的算术平方根是2, ∴ =
3、求下列各数的算术平方根:
⑴ 0.0025 ⑵ 121 ⑶ ⑷ ⑸ 7
4、求下列各式的值:
(1) (2) (3)
5、计算下列各式:
(1) — (2) — +
(3)×—×
6、求下列各等式中的正数x
(1) = 169 (2) 4 — 121 = 0
7、比较下列各组数的大小。
(1)与12 (2)与0.5
课后反思:
课题: 13.1平方根(二)
学习目标
理解平方根的概念
了解开平方的定义
掌握平方根的性质
自学指导
认真阅读72-74页内容,完成下列要求:
说明:一个正数a的算术平方根有__个,平方根有__个,并且互为____,0的平方根是___。
负数有没有平方根,为什么?
注意根号前的符号
自学20分钟后,进行展示活动
展示内容
填表:
X
8
-8
-
121
0.36
0
计算下列各式的值
(1) (2)- (3)± (4)-
平方根起源于正方形的面积,若一个正方形的面积为A,那么这个正方形的边长为多少?
判断下列说法是否正确
(1)5是25的算术平方根( )
(2)是的一个平方根( )
(3)的平方根是-4( )
(4)0的平方根与算术平方根都是0( )
5、下列各式是否有意义,为什么?
-(2)(3)(4)
6、求下列各式的x的值
(1)=25 (2)-81=0
(3)25=36 (4)2-18=0
课后反思:
课题:13.2 立方根
学习目标:
1、理解并掌握立方根的概念,会用符号表示一个数的立方根。
2、会求一个数的立方根。
自学指导:
自学课本77—78页内容,完成下列要求:
1、理解立方根的概念,理解立方与开立方是互为逆运算。
2、独立完成77页探究内容,组内合作交流,归纳出正数、负数、0的立方根的特点。
3、理解与—的相等关系。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、如果一个数的立方根等于 ,那么这个数叫做
的 或 。
2、求一个数的 的运算,叫做 。 与
互为逆运算。
3、正数的立方根是 数,负数的立方根是 数,0的立方根是 。
4、符号中,3是 ,中的 不能省略。
5、 —
6、课本79页练习1、3、4题
7、求下列各数的立方根。
(1)—8 (2) (3) ±125 (4) 81×9
8、求下列各式的值。
(1)— (2)— (3) (4)
(5)—
课后反思:
课题:13.3 实数(一)
学习目标
了解有理数、无理数、实数的概念及其分类
理解实数与数轴上的点是一一对应的关系
自学指导
认真阅读82页-84页的内容,完成下列要求:
举例说明什么是有限小数、无限小数、无限循球小数,无限不循环小数
、—、、都是无理数,那么带根号的数都是无理数吗?呢?
探究中直径为1的圆的周长是_,点O’的坐标是__
提示:举例说明什么是一一对应
展示内容
把下列各数分别填入相应的集合中
3.1415926 -8 0.6 0
有理数集合 无理数集合
正数集合 负数集合
请将数轴上的各点与下列实数对应起来
-1.5 3
-2 A 0 B C DE
3、选择,如图数轴上点A表示的是实数a,则点a到原点的距离是( )
a 0
A、a B、-a C、±a D、-|a|
4、下列说法正确的有( )个
(1)无限小数都是无理数
(2)无理数都是无限小数
(3)带根号的数都是无理数
(4)所有的有理数都可以用数轴上的点表示,反过来,数轴上的点都表示有理数
(5)所有的实数都要以用数轴上的点表示,反过来,数轴上的所有点都表示实数
A、1 B、2 C、3 D、4
5、有没有最小的正整数?有没有最小的整数?有没有最小的有理数?有没有最小的无理数?有没有最小的实数?有没有绝对值最小的实数?
课后反思:
课题:13.3 实数(二)
课型:预习展示 主备人:何立泉 审核人:何立泉 时间:
了解实数的运算法则及运算律,会进行实数的运算
明确有理数与实数的对比
自学指导
自学课本84-96页内容
回顾复习有理数的绝对值
小组交流课本84后思考题,归纳实数的相反数和绝对值的结果
明白有理数的运算法则及运算性质在进行实数的运算中,同样适用
展示内容
写出下列各数的相反数
(1)- (2) -3.14 (3)一
2、||=___ 若|a|=,则a=___
3、计算下列各式的值
(1)(+)- (2)3+2
(3)(-)-2(-)
课本86页1、2、3、4
课后反思:
