青岛版九年级数学下册 5.7 二次函数的应用(1)课件(共24张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.7 二次函数的应用(1)课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 09:09:30 | ||
图片预览





文档简介
(共24张PPT)
5.7 二次函数的应用
第1课时
1、经历数学建模的基本过程;
2、会运用二次函数求实际生活中的最值问题;
3、体会二次函数是一类最优化问题的重要数学模型,感受数学的应用价值.
学习目标
问题:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l 的变化而变化.当l是多少时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l值.
矩形场地的周长是60m,一边长为l,则另一边长为
m.场地的面积: (0S=l(30-l)
即S=-l2+30l
请同学们画出此函数的图象
知识讲解
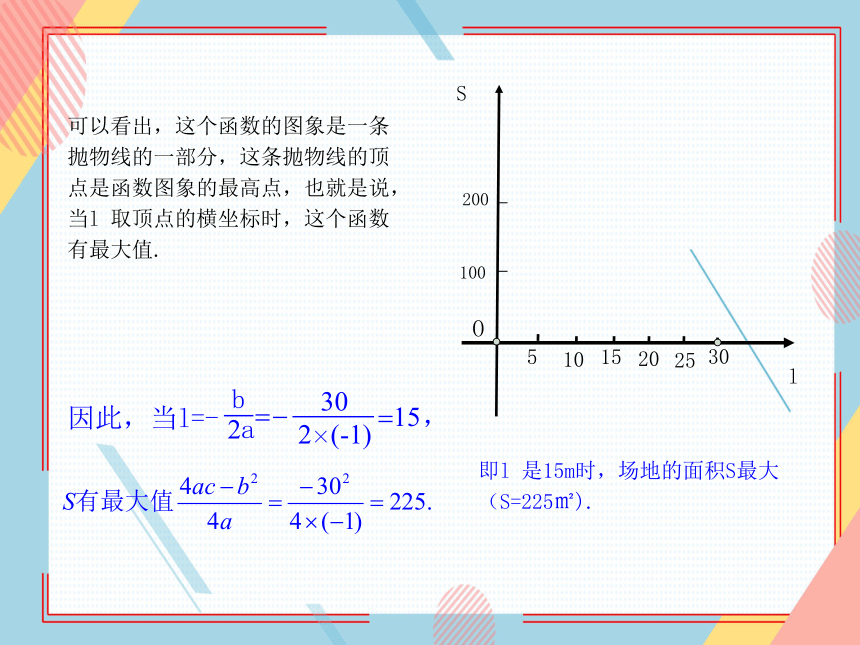
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l 取顶点的横坐标时,这个函数有最大值.
5
10
15
20
25
30
100
200
l
S
即l 是15m时,场地的面积S最大(S=225㎡).
O
30
15
2×(-1)
=
-
因此,当l=-
,
2a
b
=
一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以
当 时,二次函数y=ax2+bx+c有最小(大)值 .
归纳总结
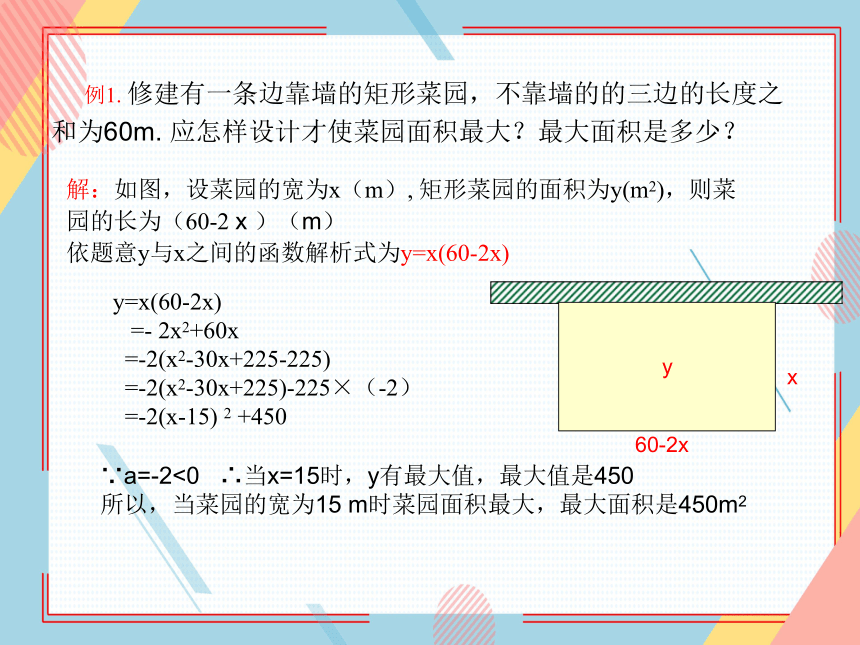
例1. 修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m. 应怎样设计才使菜园面积最大?最大面积是多少?
解:如图,设菜园的宽为x(m), 矩形菜园的面积为y(m2),则菜园的长为(60-2 x )(m)
依题意y与x之间的函数解析式为y=x(60-2x)
x
60-2x
y
y=x(60-2x)
=- 2x2+60x
=-2(x2-30x+225-225)
=-2(x2-30x+225)-225×(-2)
=-2(x-15) 2 +450
∵a=-2<0 ∴当x=15时,y有最大值,最大值是450
所以,当菜园的宽为15 m时菜园面积最大,最大面积是450m2
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
请同学们带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之
发生了变化?
典例讲解
分析:
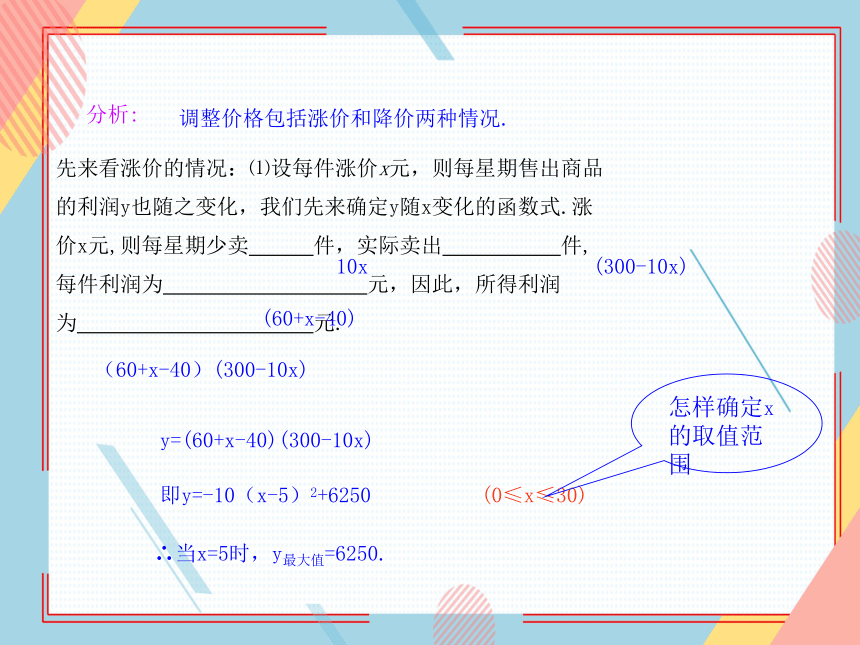
调整价格包括涨价和降价两种情况.
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y随x变化的函数式.涨
价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
y=(60+x-40)(300-10x)
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6250.
怎样确定x的取值范围
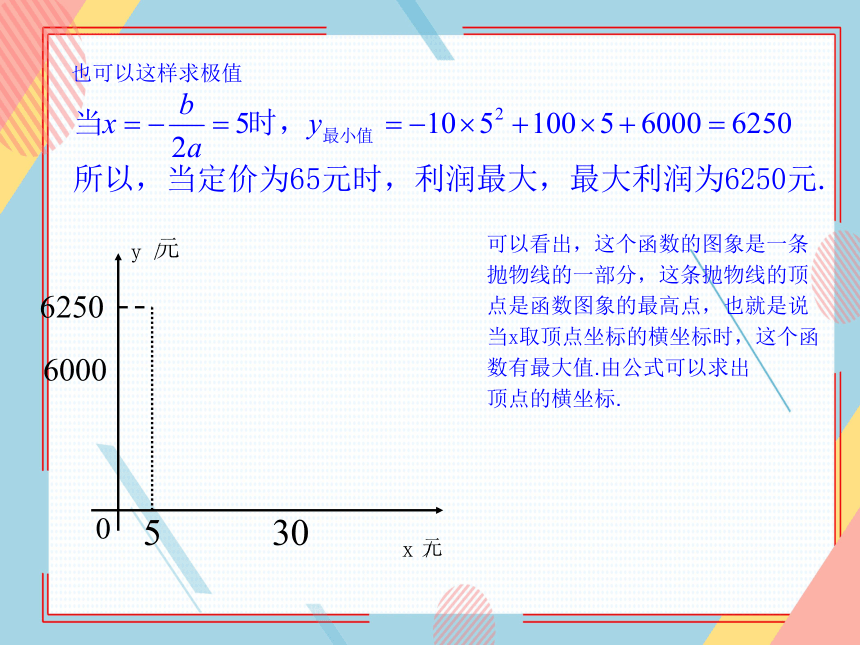
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出
顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元.
也可以这样求极值
x /
元
y /
元
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案.
解析:设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润:
y=(300+20x)(60-40-x)
=-20(x -5x+6.25)+6125
=-20(x-2.5) +6125
∴x=2.5时,y极大值=6125
你能回答了吧!
怎样确定x的取值范围
(0<x<20)
由(1)(2)的讨论及现在的销售情况,你知道应该如何
定价能使利润最大了吗
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最大值或最小值.
解决这类题目的一般步骤
1.将一条长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm2.
随堂练习
2.某商店购进一种单价为40元的篮球,如果以单价50元售
出,那么每月可售出500个,据销售经验,售价每提高1
元,销售量相应减少10个. (1)假设销售单价提高x元,那么销售每个篮球所获得的利
润是_______元,这种篮球每月的销售量是 个(用
x的代数式表示). (2)8000元是否为每月销售篮球的最大利润
如果是,说明理由,如果不是,请求出最大月利润,
此时篮球的售价应定为多少元
x+10
500 10x
8000元不是每月最大利润,最大月利润为9000元,此时篮球的售价为70元.
3.某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售单价每降低1元,平均每天就可以多售出100件.
(1)假设每件商品降低x元,商店每天销售这种小商品的利润是y元,请你写出y与x之间的函数关系式,并注明x的取值范围;
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
解析:(1)降低x元后,所销售的件数是(500+100x),
y=-100x2+600x+5500 (0<x≤11 )
(2)y=-100x2+600x+5500 (0<x≤11 )
配方得y=-100(x-3)2+6400,
当x=3时,y的最大值是6400元.
即降价为3元时,利润最大.
所以销售单价为10.5元时,最大利润为6400元.
答:销售单价为10.5元时,最大利润为6400元.
4.我市一家电子计算器专卖店每只进价13元,售价20元,多买优惠:凡是一次买10只以上的,每多买1只,所买的全部计算器每只就降低0.10元,例如,某人买20只计算器,于是每只降价0.10×(20-10)=1(元),因此,所买的全部20只计算器都按照每只19元计算,但是最低价为每只16元.
(1)求一次至少买多少只,才能以最低价购买?
(2)写出该专卖店当一次销售x(只)时,所获利润y(元)与x (只)之间的函数关系式,并写出自变量x的取值范围;
(3)若店主一次卖的只数在10只至50只之间,问一次卖多少只获得的利润最大?其最大利润为多少?
【解析】(1)设一次购买x只,才能以最低价购买,则有:
0.1(x-10)=20-16,解这个方程得x=50.
答:一次至少买50只,才能以最低价购买
(2)
(说明:因三段图象首尾相连,所以端点10、50包括在哪个区间均可)
(3)将 配方得 ,所以店主一次卖
40只时可获得最高利润,最高利润为160元.(也可用公式
法求得)
x
)
5.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且
能在当天全部售出,求第x天的收入y(元)与x(天)之
间的函数关系式?(当天收入=日销售额-日捕捞成本) 试说明(2)中的函数y随x的变化情况,并指出在第几天
y取得最大值,最大值是多少?
解:(1)该养殖场每天的捕捞量与前一天相比减少10kg; (2)由题意,得
(3)∵-2<0,y=-2x2+40x+14250=-2(x-10)2+14450, 又∵1≤x≤20且x为整数, ∴当1≤x≤10时,y随x的增大而增大; 当10≤x≤20时,y随x的增大而减小; 当x=10时即在第10天,y取得最大值,最大值为14450元.
1.主要学习了如何将实际问题转化为数学问题,特别是如何利用二次函数的有关性质解决实际问题的方法;
2.利用二次函数解决实际问题时,写出二次函数表达式是解决问题的关键.
本课小结
5.7 二次函数的应用
第1课时
1、经历数学建模的基本过程;
2、会运用二次函数求实际生活中的最值问题;
3、体会二次函数是一类最优化问题的重要数学模型,感受数学的应用价值.
学习目标
问题:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l 的变化而变化.当l是多少时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l值.
矩形场地的周长是60m,一边长为l,则另一边长为
m.场地的面积: (0
即S=-l2+30l
请同学们画出此函数的图象
知识讲解
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l 取顶点的横坐标时,这个函数有最大值.
5
10
15
20
25
30
100
200
l
S
即l 是15m时,场地的面积S最大(S=225㎡).
O
30
15
2×(-1)
=
-
因此,当l=-
,
2a
b
=
一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以
当 时,二次函数y=ax2+bx+c有最小(大)值 .
归纳总结
例1. 修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m. 应怎样设计才使菜园面积最大?最大面积是多少?
解:如图,设菜园的宽为x(m), 矩形菜园的面积为y(m2),则菜园的长为(60-2 x )(m)
依题意y与x之间的函数解析式为y=x(60-2x)
x
60-2x
y
y=x(60-2x)
=- 2x2+60x
=-2(x2-30x+225-225)
=-2(x2-30x+225)-225×(-2)
=-2(x-15) 2 +450
∵a=-2<0 ∴当x=15时,y有最大值,最大值是450
所以,当菜园的宽为15 m时菜园面积最大,最大面积是450m2
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
请同学们带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之
发生了变化?
典例讲解
分析:
调整价格包括涨价和降价两种情况.
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y随x变化的函数式.涨
价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
y=(60+x-40)(300-10x)
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6250.
怎样确定x的取值范围
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出
顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元.
也可以这样求极值
x /
元
y /
元
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案.
解析:设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润:
y=(300+20x)(60-40-x)
=-20(x -5x+6.25)+6125
=-20(x-2.5) +6125
∴x=2.5时,y极大值=6125
你能回答了吧!
怎样确定x的取值范围
(0<x<20)
由(1)(2)的讨论及现在的销售情况,你知道应该如何
定价能使利润最大了吗
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最大值或最小值.
解决这类题目的一般步骤
1.将一条长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm2.
随堂练习
2.某商店购进一种单价为40元的篮球,如果以单价50元售
出,那么每月可售出500个,据销售经验,售价每提高1
元,销售量相应减少10个. (1)假设销售单价提高x元,那么销售每个篮球所获得的利
润是_______元,这种篮球每月的销售量是 个(用
x的代数式表示). (2)8000元是否为每月销售篮球的最大利润
如果是,说明理由,如果不是,请求出最大月利润,
此时篮球的售价应定为多少元
x+10
500 10x
8000元不是每月最大利润,最大月利润为9000元,此时篮球的售价为70元.
3.某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售单价每降低1元,平均每天就可以多售出100件.
(1)假设每件商品降低x元,商店每天销售这种小商品的利润是y元,请你写出y与x之间的函数关系式,并注明x的取值范围;
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
解析:(1)降低x元后,所销售的件数是(500+100x),
y=-100x2+600x+5500 (0<x≤11 )
(2)y=-100x2+600x+5500 (0<x≤11 )
配方得y=-100(x-3)2+6400,
当x=3时,y的最大值是6400元.
即降价为3元时,利润最大.
所以销售单价为10.5元时,最大利润为6400元.
答:销售单价为10.5元时,最大利润为6400元.
4.我市一家电子计算器专卖店每只进价13元,售价20元,多买优惠:凡是一次买10只以上的,每多买1只,所买的全部计算器每只就降低0.10元,例如,某人买20只计算器,于是每只降价0.10×(20-10)=1(元),因此,所买的全部20只计算器都按照每只19元计算,但是最低价为每只16元.
(1)求一次至少买多少只,才能以最低价购买?
(2)写出该专卖店当一次销售x(只)时,所获利润y(元)与x (只)之间的函数关系式,并写出自变量x的取值范围;
(3)若店主一次卖的只数在10只至50只之间,问一次卖多少只获得的利润最大?其最大利润为多少?
【解析】(1)设一次购买x只,才能以最低价购买,则有:
0.1(x-10)=20-16,解这个方程得x=50.
答:一次至少买50只,才能以最低价购买
(2)
(说明:因三段图象首尾相连,所以端点10、50包括在哪个区间均可)
(3)将 配方得 ,所以店主一次卖
40只时可获得最高利润,最高利润为160元.(也可用公式
法求得)
x
)
5.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且
能在当天全部售出,求第x天的收入y(元)与x(天)之
间的函数关系式?(当天收入=日销售额-日捕捞成本) 试说明(2)中的函数y随x的变化情况,并指出在第几天
y取得最大值,最大值是多少?
解:(1)该养殖场每天的捕捞量与前一天相比减少10kg; (2)由题意,得
(3)∵-2<0,y=-2x2+40x+14250=-2(x-10)2+14450, 又∵1≤x≤20且x为整数, ∴当1≤x≤10时,y随x的增大而增大; 当10≤x≤20时,y随x的增大而减小; 当x=10时即在第10天,y取得最大值,最大值为14450元.
1.主要学习了如何将实际问题转化为数学问题,特别是如何利用二次函数的有关性质解决实际问题的方法;
2.利用二次函数解决实际问题时,写出二次函数表达式是解决问题的关键.
本课小结
