2022年“五一假期”人教版八年级下册第18章《平行四边形》知识巩固训练卷(word版 含解析)
文档属性
| 名称 | 2022年“五一假期”人教版八年级下册第18章《平行四边形》知识巩固训练卷(word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览


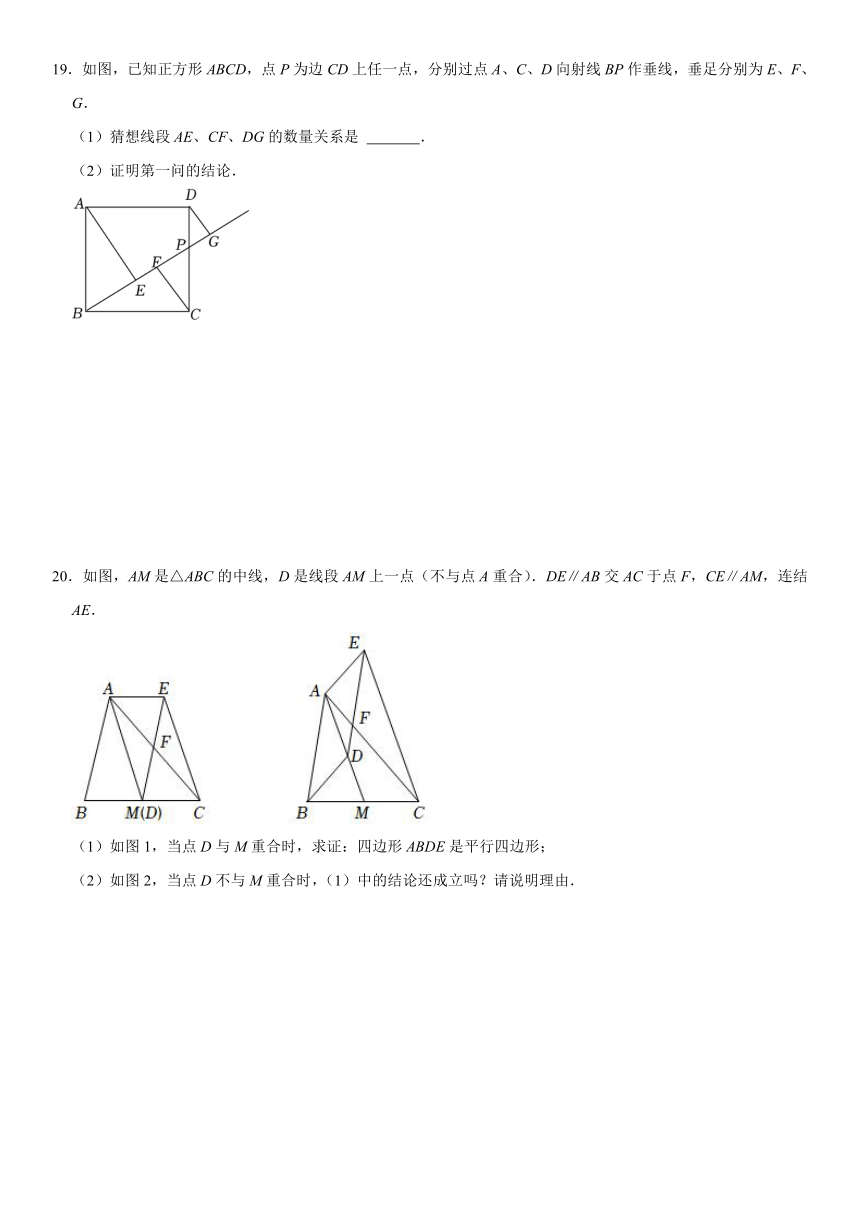

文档简介
2022年“五一假期”八年级下册数学第18章《平行四边形》知识巩固训练卷
一.选择题
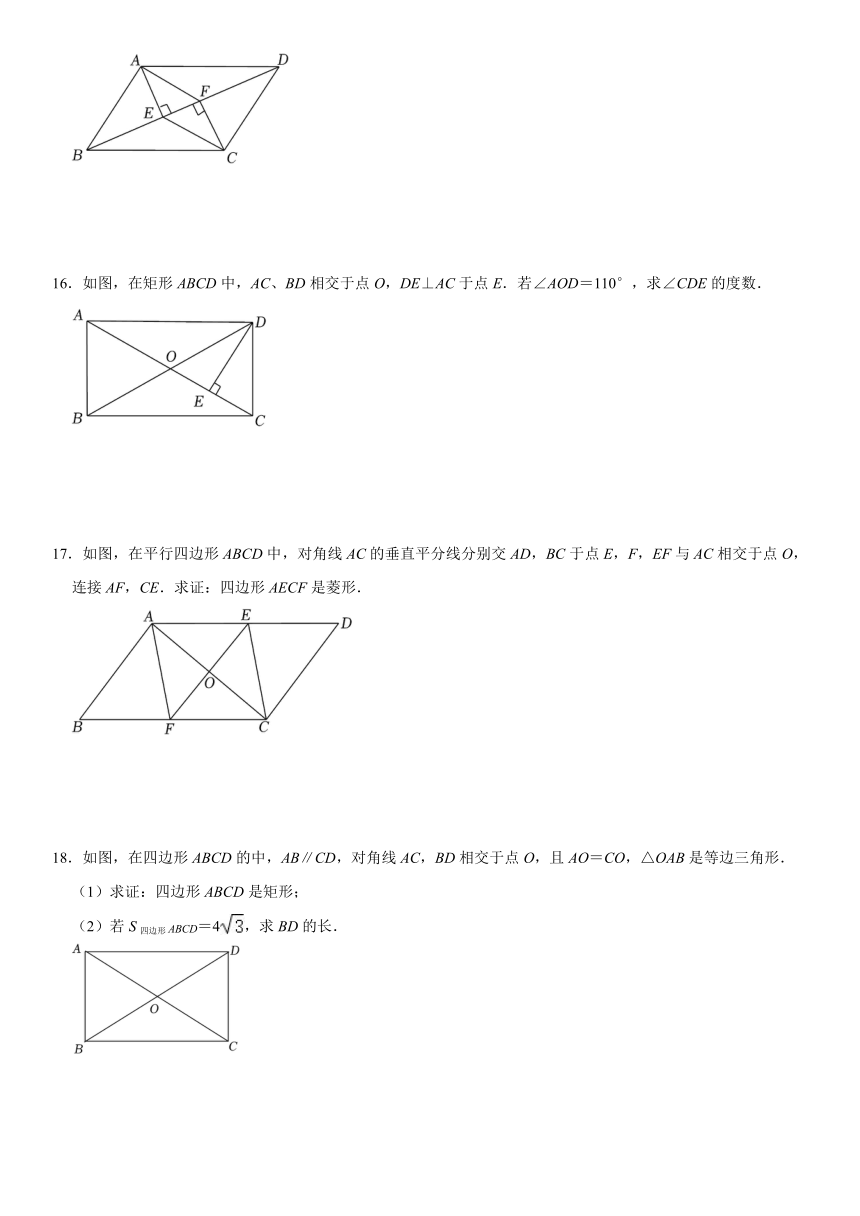
1.不能判定一个四边形是平行四边形的条件是( )
A.两组对边分别平行 B.一组对边平行,一组对角相等
C.一组对边平行且相等 D.一组对边平行,另一组对边相等
2.如图,已知平行四边形ABCD的周长等于22cm,AC=8cm,则△ABC的周长是( )
A.11cm B.15cm C.16cm D.19cm
3.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
4.如图,DE是△ABC的中位线,若DE=4,则BC的长为( )
A.8 B.7 C.6 D.7.5
5.如图,在平行四边形ABCD中,GH∥AB,EF∥BC,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.3对 B.2对 C.1对 D.0对
6.如图,四边形ABCD为正方形,O为AC、BD的交点,∠CED=90°,OE=2,若CE DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
7.如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是( )
A.2.5 B.5 C.2.4 D.1.2
8.如图,在菱形ABCD中,AB=6cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB.CB方向向点B匀速移动,点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A.1 B.1.3 C.1.5 D.2
二.填空题
9.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AB=2,则CD= .
10. ABCD中,若∠A:∠B=2:3,则∠C= .
11.若正方形ABCD的周长为8,则对角线AC的长为 .
12.如图,在 ABCD中,对角线AC、BD相交于点O.如果AC=6,BD=8,AB=x,那么x的取值范围是 .
13.在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,2)三点,现以A,B,C,D为顶点作平行四边形,则第四个顶点D的坐标是 .
14.如图,在 ABCD中,已知AE⊥BC于点E,AF⊥CD于点F,若AF=4,DF=CE=3,则 ABCD的面积为 .
三.解答题
15.如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,E,F分别是垂足.求证:AF∥CE.
16.如图,在矩形ABCD中,AC、BD相交于点O,DE⊥AC于点E.若∠AOD=110°,求∠CDE的度数.
17.如图,在平行四边形ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,EF与AC相交于点O,连接AF,CE.求证:四边形AECF是菱形.
18.如图,在四边形ABCD的中,AB∥CD,对角线AC,BD相交于点O,且AO=CO,△OAB是等边三角形.
(1)求证:四边形ABCD是矩形;
(2)若S四边形ABCD=4,求BD的长.
19.如图,已知正方形ABCD,点P为边CD上任一点,分别过点A、C、D向射线BP作垂线,垂足分别为E、F、G.
(1)猜想线段AE、CF、DG的数量关系是 .
(2)证明第一问的结论.
20.如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
参考答案
一.选择题
1.【解答】解:A、两组对边分别平行的四边形是平行四边形,故选项A不符合题意;
B、一组对边平行,一组对角相等的四边形是平行四边形,故选项B不符合题意;
C、一组对边平行且相等的四边形是平行四边形,故选项C不符合题意;
D、一组对边平行,另一组对边相等的四边形不一定是平行四边形,故选项D符合题意;
故选:D.
2.【解答】解:∵ ABCD的周长是22cm,
∴AB+BC=11cm,
∵△AC=8cm,
∴△ABC的周长为AC+(AB+BC)=8+11=19(cm),
故选:D.
3.【解答】解:A、矩形、平行四边形的对边都是相等的,故本选项不符合;
B、矩形、平行四边形的对角都是相等的,故本选项不符合;
C、矩形、平行四边形的对角线都是互相平分的,故本选项不符合;
D、矩形的对角线相等,平行四边形的对角线不一定相等,故本选项符合;
故选:D.
4.【解答】解:∵DE是△ABC的中位线,DE=4,
∴BC=2DE=8,
故选:A.
5.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,S△ABD=S△CBD.
∵GH∥AB,EF∥BC,
∴GH∥AB∥CD,EF∥BC∥AD,
∴四边形ABHG、四边形CDGH、四边形BHPE、四边形CHPF、四边形AEPG、四边形DFPG、四边形AEFD、四边形BCFE都是平行四边形,
∵BP是平行四边形BEPH的对角线,
∴S△BEP=S△BHP,
∵PD是平行四边形GPFD的对角线,
∴S△GPD=S△FPD.
∴S△ABD﹣S△BEP﹣S△GPD=S△BCD﹣S△BHP﹣S△PFD,
即S AEPG=S HCFP,
∴S ABHG=S BCFE,
同理S AEFD=S HCDG.
即:S ABHG=S BCFE,S AGPE=S HCFP,S AEFD=S HCDG.
故选:A.
6.【解答】解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选B.
7.【解答】解:如图,连接CP.
∵∠C=90°,AC=3,BC=4,
∴AB===5,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFPE是矩形,
∴EF=CP,
由垂线段最短可得CP⊥AB时,线段EF的值最小,
此时,S△ABC=BC AC=AB CP,
即×4×3=×5 CP,
解得CP=2.4.
故选:C.
8.【解答】解:延长AB至M,使BM=AE,连FM,
∵四边形ABCD是菱形,∠ADC=120°,
∴AB=AD,∠A=60°,
∴∠AED+∠ADE=120°,
∵BM=AE,
∴AD=ME,
∵△DEF为等边三角形,
∴∠DEF=60°,
∴∠MEF+∠AED=120°
∴∠MEF=∠ADE,
在△ADE和△MEF中
,
∴△DAE≌△EMF(SAS),
∴AE=MF,∠M=∠A=60°,
又∵BM=AE,
∴△BMF是等边三角形,
∴BF=AE,
∵AE=t,CF=2t,
∴BC=CF+BF=3t,
∵BC=6,
∴t=2.
故选D.
二.填空题
9.【解答】解:∵∠ACB=90°,D为AB中点,AB=2,
∴CD=AB=1,
故答案为:1.
10.【解答】解:依题意设∠A=2x,∠B=3x,
由平行四边形的性质,得∠A+∠B=180°,
∴2x+3x=180°,解得x=36°,
∴∠A=2x=72°,
∵∠A=∠C,
∴∠C=72°.
故答案为72°.
11.【解答】解:设正方形的边长为a,
∵正方形ABCD的周长为8,
∴4a=8,即a=2,
∴对角线AC=.
故答案为:2.
12.【解答】解:在平行四边形ABCD中,AC=6,BD=8,
∴OA=AC=3,OB=BD=4,
∵AB=x,
在△AOB中,由三角形的三边关系得:
∴x的取值范围是:1<x<7.
故答案为1<x<7.
13.【解答】解:如图,
当以AC为对角线,此时D(﹣1,2);
当以AB为对角线时,此时D′(﹣3,﹣2);
当以BC为对角线时,此时点D″(7,2).
则第四个顶点D的坐标是(﹣1.2)或(﹣3,﹣2)或(7,2).
故答案为:(﹣1.2)或(﹣3,﹣2)或(7,2).
14.【解答】解:设CF=x,则AB=CD=3+x,
∵AF⊥CD,AF=4,DF=3,
∴AD=,
∵四边形ABCD是平行四边形,
∴AD=BC=5,
∴BE=5﹣3=2,
∵ ABCD的面积=BC AE=CD AF,
即5AE=4(x+3),
∴AE=,
在Rt△ABE中,由勾股定理得:AB2=AE2+BE2,
(x+3)2=22+,
(x+3)2=,
解得:x1=,x2=﹣,
∴ ABCD的面积=CD AF=4(+3)=.
故答案为:.
三.解答题
15.【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
16.【解答】解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故∠CDE的度数为35°.
17.【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
又∵EF垂直平分AC,
∴OA=OC.EA=EC,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AECF是平行四边形,
∵EA=EC,
∴平行四边形AECF是菱形.
18.【解答】(1)证明:∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△COD中,
,
∴△AOB≌△COD(ASA),
∴BO=DO,AB=CD,
∴四边形ABCD是平行四边形,
∵△OAB是等边三角形,
∴OA=OB,
∴OA=OC=OB=OD,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵△OAB是等边三角形,
∴AB=OA=OB,
∵AO=CO,
∴AC=2OA,
∴AC=2AB,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BC===AB,
∵S四边形ABCD=AB BC=AB2=4,
∴AB2=4,
∴AB==2,
∴OB=2,
∴BD=2OB=4.
19.【解答】(1)解:AE=CF+DG;
故答案为:AE=CF+DG;
(2)证明:如图1,过点D作DH⊥CF交CF的延长线于点H,
则∠CHD=∠AEB=90°,
∵四边形ABCD为正方形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CPF,
∵AE⊥BP,CF⊥BP,DG⊥BP,
∴∠AEB=∠CFP=∠DGF=90°,
∴∠ABE+∠BAE=∠CPF+∠DCH=90°,
∴∠BAE=∠DCH.
在△ABE和△CDH中,
,
∴△ABE≌△CDH(AAS),
∴AE=CH,
∵∠CHD=∠HFG=∠DGF=90°,
∴四边形HFGD为矩形,
∴HF=DG,
∴AE=CH=CF+HF=CF+DG.
20.【解答】(1)证明:如图1,∵AM是△ABC的中线,D与M重合,
∴DC=BD,
∵DE∥AB,
∴∠EDC=∠B,
∵CE∥AM,即CE∥AD,
∴∠ECD=∠ADB,
在△ECD和△ADB中,
,
∴△ECD≌△ADB(ASA),
∴DE=AB,
∴四边形ABDE是平行四边形.
(2)成立,理由如下:
如图2,过点M作MG∥AB交CG于点G,
∵DE∥AB,
∴MG∥DE,
∵CE∥AM,
∴四边形DEGM是平行四边形,
∴MG=DE,
由(1)得MG=AB,
∴DE=AB,
∴四边形ABDE是平行四边形.
一.选择题
1.不能判定一个四边形是平行四边形的条件是( )
A.两组对边分别平行 B.一组对边平行,一组对角相等
C.一组对边平行且相等 D.一组对边平行,另一组对边相等
2.如图,已知平行四边形ABCD的周长等于22cm,AC=8cm,则△ABC的周长是( )
A.11cm B.15cm C.16cm D.19cm
3.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
4.如图,DE是△ABC的中位线,若DE=4,则BC的长为( )
A.8 B.7 C.6 D.7.5
5.如图,在平行四边形ABCD中,GH∥AB,EF∥BC,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.3对 B.2对 C.1对 D.0对
6.如图,四边形ABCD为正方形,O为AC、BD的交点,∠CED=90°,OE=2,若CE DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
7.如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是( )
A.2.5 B.5 C.2.4 D.1.2
8.如图,在菱形ABCD中,AB=6cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB.CB方向向点B匀速移动,点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A.1 B.1.3 C.1.5 D.2
二.填空题
9.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AB=2,则CD= .
10. ABCD中,若∠A:∠B=2:3,则∠C= .
11.若正方形ABCD的周长为8,则对角线AC的长为 .
12.如图,在 ABCD中,对角线AC、BD相交于点O.如果AC=6,BD=8,AB=x,那么x的取值范围是 .
13.在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,2)三点,现以A,B,C,D为顶点作平行四边形,则第四个顶点D的坐标是 .
14.如图,在 ABCD中,已知AE⊥BC于点E,AF⊥CD于点F,若AF=4,DF=CE=3,则 ABCD的面积为 .
三.解答题
15.如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,E,F分别是垂足.求证:AF∥CE.
16.如图,在矩形ABCD中,AC、BD相交于点O,DE⊥AC于点E.若∠AOD=110°,求∠CDE的度数.
17.如图,在平行四边形ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,EF与AC相交于点O,连接AF,CE.求证:四边形AECF是菱形.
18.如图,在四边形ABCD的中,AB∥CD,对角线AC,BD相交于点O,且AO=CO,△OAB是等边三角形.
(1)求证:四边形ABCD是矩形;
(2)若S四边形ABCD=4,求BD的长.
19.如图,已知正方形ABCD,点P为边CD上任一点,分别过点A、C、D向射线BP作垂线,垂足分别为E、F、G.
(1)猜想线段AE、CF、DG的数量关系是 .
(2)证明第一问的结论.
20.如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
参考答案
一.选择题
1.【解答】解:A、两组对边分别平行的四边形是平行四边形,故选项A不符合题意;
B、一组对边平行,一组对角相等的四边形是平行四边形,故选项B不符合题意;
C、一组对边平行且相等的四边形是平行四边形,故选项C不符合题意;
D、一组对边平行,另一组对边相等的四边形不一定是平行四边形,故选项D符合题意;
故选:D.
2.【解答】解:∵ ABCD的周长是22cm,
∴AB+BC=11cm,
∵△AC=8cm,
∴△ABC的周长为AC+(AB+BC)=8+11=19(cm),
故选:D.
3.【解答】解:A、矩形、平行四边形的对边都是相等的,故本选项不符合;
B、矩形、平行四边形的对角都是相等的,故本选项不符合;
C、矩形、平行四边形的对角线都是互相平分的,故本选项不符合;
D、矩形的对角线相等,平行四边形的对角线不一定相等,故本选项符合;
故选:D.
4.【解答】解:∵DE是△ABC的中位线,DE=4,
∴BC=2DE=8,
故选:A.
5.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,S△ABD=S△CBD.
∵GH∥AB,EF∥BC,
∴GH∥AB∥CD,EF∥BC∥AD,
∴四边形ABHG、四边形CDGH、四边形BHPE、四边形CHPF、四边形AEPG、四边形DFPG、四边形AEFD、四边形BCFE都是平行四边形,
∵BP是平行四边形BEPH的对角线,
∴S△BEP=S△BHP,
∵PD是平行四边形GPFD的对角线,
∴S△GPD=S△FPD.
∴S△ABD﹣S△BEP﹣S△GPD=S△BCD﹣S△BHP﹣S△PFD,
即S AEPG=S HCFP,
∴S ABHG=S BCFE,
同理S AEFD=S HCDG.
即:S ABHG=S BCFE,S AGPE=S HCFP,S AEFD=S HCDG.
故选:A.
6.【解答】解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选B.
7.【解答】解:如图,连接CP.
∵∠C=90°,AC=3,BC=4,
∴AB===5,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFPE是矩形,
∴EF=CP,
由垂线段最短可得CP⊥AB时,线段EF的值最小,
此时,S△ABC=BC AC=AB CP,
即×4×3=×5 CP,
解得CP=2.4.
故选:C.
8.【解答】解:延长AB至M,使BM=AE,连FM,
∵四边形ABCD是菱形,∠ADC=120°,
∴AB=AD,∠A=60°,
∴∠AED+∠ADE=120°,
∵BM=AE,
∴AD=ME,
∵△DEF为等边三角形,
∴∠DEF=60°,
∴∠MEF+∠AED=120°
∴∠MEF=∠ADE,
在△ADE和△MEF中
,
∴△DAE≌△EMF(SAS),
∴AE=MF,∠M=∠A=60°,
又∵BM=AE,
∴△BMF是等边三角形,
∴BF=AE,
∵AE=t,CF=2t,
∴BC=CF+BF=3t,
∵BC=6,
∴t=2.
故选D.
二.填空题
9.【解答】解:∵∠ACB=90°,D为AB中点,AB=2,
∴CD=AB=1,
故答案为:1.
10.【解答】解:依题意设∠A=2x,∠B=3x,
由平行四边形的性质,得∠A+∠B=180°,
∴2x+3x=180°,解得x=36°,
∴∠A=2x=72°,
∵∠A=∠C,
∴∠C=72°.
故答案为72°.
11.【解答】解:设正方形的边长为a,
∵正方形ABCD的周长为8,
∴4a=8,即a=2,
∴对角线AC=.
故答案为:2.
12.【解答】解:在平行四边形ABCD中,AC=6,BD=8,
∴OA=AC=3,OB=BD=4,
∵AB=x,
在△AOB中,由三角形的三边关系得:
∴x的取值范围是:1<x<7.
故答案为1<x<7.
13.【解答】解:如图,
当以AC为对角线,此时D(﹣1,2);
当以AB为对角线时,此时D′(﹣3,﹣2);
当以BC为对角线时,此时点D″(7,2).
则第四个顶点D的坐标是(﹣1.2)或(﹣3,﹣2)或(7,2).
故答案为:(﹣1.2)或(﹣3,﹣2)或(7,2).
14.【解答】解:设CF=x,则AB=CD=3+x,
∵AF⊥CD,AF=4,DF=3,
∴AD=,
∵四边形ABCD是平行四边形,
∴AD=BC=5,
∴BE=5﹣3=2,
∵ ABCD的面积=BC AE=CD AF,
即5AE=4(x+3),
∴AE=,
在Rt△ABE中,由勾股定理得:AB2=AE2+BE2,
(x+3)2=22+,
(x+3)2=,
解得:x1=,x2=﹣,
∴ ABCD的面积=CD AF=4(+3)=.
故答案为:.
三.解答题
15.【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
16.【解答】解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故∠CDE的度数为35°.
17.【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
又∵EF垂直平分AC,
∴OA=OC.EA=EC,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AECF是平行四边形,
∵EA=EC,
∴平行四边形AECF是菱形.
18.【解答】(1)证明:∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△COD中,
,
∴△AOB≌△COD(ASA),
∴BO=DO,AB=CD,
∴四边形ABCD是平行四边形,
∵△OAB是等边三角形,
∴OA=OB,
∴OA=OC=OB=OD,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵△OAB是等边三角形,
∴AB=OA=OB,
∵AO=CO,
∴AC=2OA,
∴AC=2AB,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BC===AB,
∵S四边形ABCD=AB BC=AB2=4,
∴AB2=4,
∴AB==2,
∴OB=2,
∴BD=2OB=4.
19.【解答】(1)解:AE=CF+DG;
故答案为:AE=CF+DG;
(2)证明:如图1,过点D作DH⊥CF交CF的延长线于点H,
则∠CHD=∠AEB=90°,
∵四边形ABCD为正方形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CPF,
∵AE⊥BP,CF⊥BP,DG⊥BP,
∴∠AEB=∠CFP=∠DGF=90°,
∴∠ABE+∠BAE=∠CPF+∠DCH=90°,
∴∠BAE=∠DCH.
在△ABE和△CDH中,
,
∴△ABE≌△CDH(AAS),
∴AE=CH,
∵∠CHD=∠HFG=∠DGF=90°,
∴四边形HFGD为矩形,
∴HF=DG,
∴AE=CH=CF+HF=CF+DG.
20.【解答】(1)证明:如图1,∵AM是△ABC的中线,D与M重合,
∴DC=BD,
∵DE∥AB,
∴∠EDC=∠B,
∵CE∥AM,即CE∥AD,
∴∠ECD=∠ADB,
在△ECD和△ADB中,
,
∴△ECD≌△ADB(ASA),
∴DE=AB,
∴四边形ABDE是平行四边形.
(2)成立,理由如下:
如图2,过点M作MG∥AB交CG于点G,
∵DE∥AB,
∴MG∥DE,
∵CE∥AM,
∴四边形DEGM是平行四边形,
∴MG=DE,
由(1)得MG=AB,
∴DE=AB,
∴四边形ABDE是平行四边形.
