2022年“五一假期”人教版八年级下册第16章《二次根式》知识巩固训练卷(word版 含解析)
文档属性
| 名称 | 2022年“五一假期”人教版八年级下册第16章《二次根式》知识巩固训练卷(word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 260.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 17:12:15 | ||
图片预览

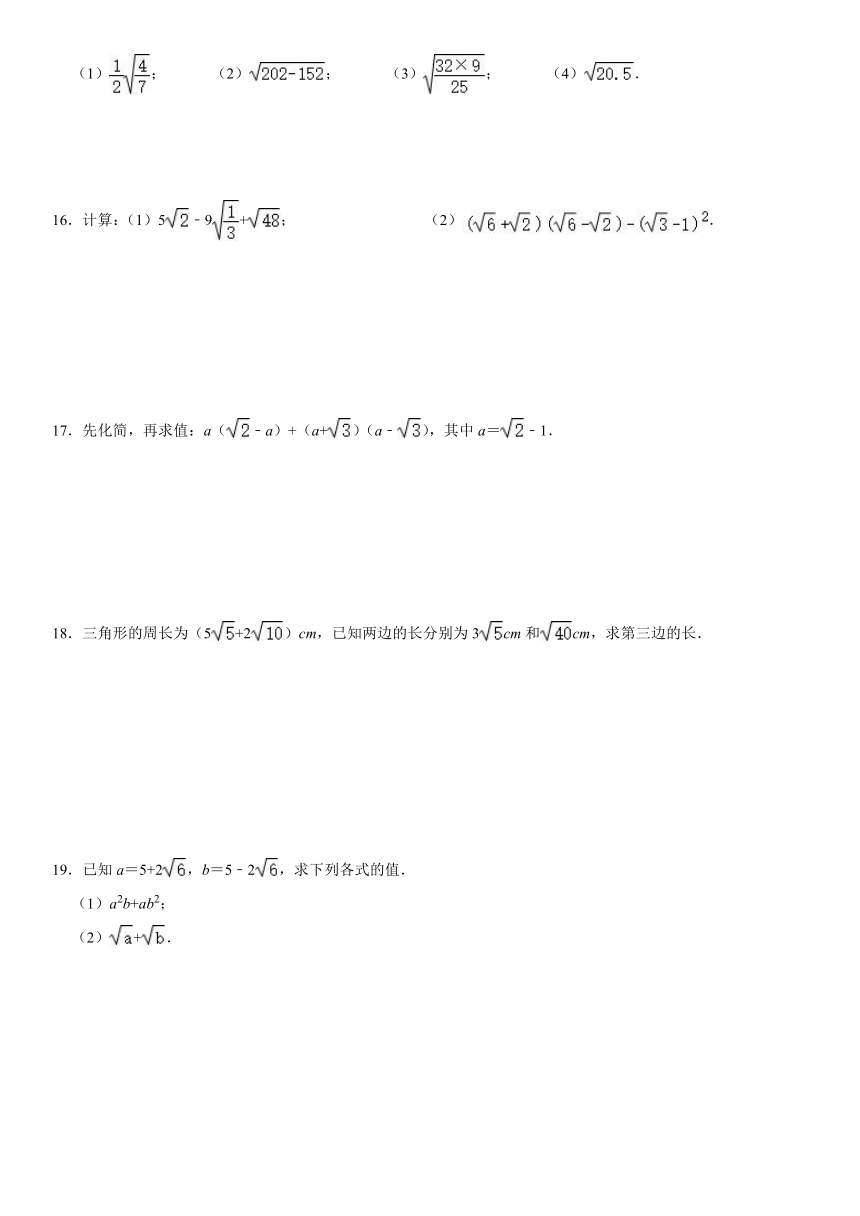

文档简介
2022年“五一假期”八年级下册数学第16章《二次根式》知识巩固训练卷
一.选择题
1.下列各式中,,,,,,其中一定是二次根式的有( )
A.1个 B.2个 C.3个 D.4个
2.下列x的取值中,可以使有意义的是( )
A.2022 B.8 C.9 D.0
3.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
4.下列二次根式能与合并的是( )
A. B. C. D.
5.下列计算正确的是( )
A.= B.4﹣3=1 C.﹣= D.3+2=5
6.若=a,=b,则=( )
A. B. C.ab D.a+b
7.已知n是正整数,是整数,则n的最小值为( )
A.2 B.3 C.4 D.5
8.的结果是( )
A. B.3 C.﹣3 D.
二.填空题
9.化简的结果是 .
10.要使代数式有意义,则x的取值范围是 .
11.已知长方形的面积是48cm2,其中一边的长是,则该长方形的周长为 .
12.实数a,b在数轴上的位置如图所示,则化简的结果是 .
13.若,,则代数式x2﹣y2的值为 .
14.对于任意的正数m,n定义运算*为:m*n=,计算(3*2)+(8*12)的结果为 .
三.解答题
15.化简:
(1); (2); (3); (4).
16.计算:(1)5﹣9+; (2).
17.先化简,再求值:a(﹣a)+(a+)(a﹣),其中a=﹣1.
18.三角形的周长为(5+2)cm,已知两边的长分别为3cm和cm,求第三边的长.
19.已知a=5+2,b=5﹣2,求下列各式的值.
(1)a2b+ab2;
(2)+.
20.材料一:有这样一类题目:将化简,如果你能找到两个数m、n,使m2+n2=a且mm=,则将a±2将变成m2+n2±2n,即变成(m±n)2开方,从而使得化简.
例如,5±2=3+2±2=()2+()2×=(±)2,所以==±;
材料二:在进行二次根式的化简时,我们有时会碰到如,,这样的式子,其实我们还可以将其进一步化简:==(一);==(二);===﹣1(三).以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:====﹣1(四);
请根据材料解答下列问题:
(1)= ;= .
(2)化简:+++…+.
参考答案
一.选择题
1.【解答】解:是二次根式的有、,共2个;
故选:B.
2.【解答】解:根据二次根式有意义的条件得:7﹣x≥0,
∴x≤7,
∴符合题意的是0,
故选:D.
3.【解答】解:∵=,
∴选项A不符合题意;
∵=2,
∴选项B不符合题意;
∵已是最简二次根式,
∴选项C符合题意;
∵=2,
∴选项D不符合题意;
故选:C.
4.【解答】解:A、=2与2不是同类二次根式,不能合并,故A不符合题意;
B、=2与2不是同类二次根式,不能合并,故B不符合题意;
C、=3与2是同类二次根式,能合并,故C符合题意;
D、与2不是同类二次根式,不能合并,故D不符合题意;
故选:C.
5.【解答】解:A.+无法合并,故此选项不合题意;
B.4﹣3=,故此选项不合题意;
C.﹣=,故此选项符合题意;
D.3+2无法合并,故此选项不合题意;
故选:C.
6.【解答】解:∵=a,=b,
∴==×=ab.
故选:C.
7.【解答】解:=2,
∵是整数,
∴n的最小值是5,
故选:D.
8.【解答】解:原式=[(+3)(﹣3)]2019(+3)
=(10﹣9)2019(+3)
=+3,
故选:D.
二.填空题
9.【解答】解:(﹣)2=3.
故答案为:3.
10.【解答】解:由题意得:4﹣2x≥0且x+1≠0,
解得:x≤2且x≠﹣1,
故答案为:x≤2且x≠﹣1.
11.【解答】解:设长方形的另外一边为x(cm),
∴x==6(cm),
∴周长为:2(6+)=20(cm),
故答案为:20(cm).
12.【解答】解:由数轴可得,a<0,b>0,a﹣b<0,
∴原式=|a|﹣|b|﹣|a﹣b|
=﹣a﹣b﹣(﹣a+b)
=﹣a﹣b+a﹣b
=﹣2b,
故答案为:﹣2b.
13.【解答】解:∵,,
∴x+y=2,x﹣y=2,
∴x2﹣y2
=(x+y)(x﹣y)
=2×2
=4,
故答案为:4.
14.【解答】解:∵3>2,8<12,
∴原式=(﹣)+(+)
=﹣+2+2
=3+,
故答案为:3+.
三.解答题
15.【解答】解:(1)原式=×
=.
(2)原式=
=5.
(3)原式=
=.
(4)原式=
=.
16.【解答】解:(1)原式=5﹣3+4
=5+.
(2)原式=6﹣2﹣(3﹣2+1)
=4﹣(4﹣2)
=4﹣4+2
=2.
17.【解答】解:原式=
=a﹣3,
当a=﹣1时,
原式=(﹣1)﹣3
=2﹣﹣3
=﹣1﹣.
18.【解答】解:∵三角形周长为,两边长为,
∴第三边长为:==(cm),
答:第三边长为2cm.
19.【解答】解:∵a=5+2,b=5﹣2,
∴a+b=10,ab=1,
(1)a2b+ab2
=ab(a+b)
=1×10
=10;
(2)(+)2
=a+b+2
=10+2×
=12,
∵+≥0,
∴+==2.
20.【解答】解:(1)∵3﹣2=2+1﹣2=(﹣1)2,
∴==﹣1,
∵4+2=3+1+2=(+1)2,
∴==+1,
故答案为:﹣1,+1;
(2)+++…+
=++ +
=﹣1+﹣+﹣+ +﹣
=﹣1+.
一.选择题
1.下列各式中,,,,,,其中一定是二次根式的有( )
A.1个 B.2个 C.3个 D.4个
2.下列x的取值中,可以使有意义的是( )
A.2022 B.8 C.9 D.0
3.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
4.下列二次根式能与合并的是( )
A. B. C. D.
5.下列计算正确的是( )
A.= B.4﹣3=1 C.﹣= D.3+2=5
6.若=a,=b,则=( )
A. B. C.ab D.a+b
7.已知n是正整数,是整数,则n的最小值为( )
A.2 B.3 C.4 D.5
8.的结果是( )
A. B.3 C.﹣3 D.
二.填空题
9.化简的结果是 .
10.要使代数式有意义,则x的取值范围是 .
11.已知长方形的面积是48cm2,其中一边的长是,则该长方形的周长为 .
12.实数a,b在数轴上的位置如图所示,则化简的结果是 .
13.若,,则代数式x2﹣y2的值为 .
14.对于任意的正数m,n定义运算*为:m*n=,计算(3*2)+(8*12)的结果为 .
三.解答题
15.化简:
(1); (2); (3); (4).
16.计算:(1)5﹣9+; (2).
17.先化简,再求值:a(﹣a)+(a+)(a﹣),其中a=﹣1.
18.三角形的周长为(5+2)cm,已知两边的长分别为3cm和cm,求第三边的长.
19.已知a=5+2,b=5﹣2,求下列各式的值.
(1)a2b+ab2;
(2)+.
20.材料一:有这样一类题目:将化简,如果你能找到两个数m、n,使m2+n2=a且mm=,则将a±2将变成m2+n2±2n,即变成(m±n)2开方,从而使得化简.
例如,5±2=3+2±2=()2+()2×=(±)2,所以==±;
材料二:在进行二次根式的化简时,我们有时会碰到如,,这样的式子,其实我们还可以将其进一步化简:==(一);==(二);===﹣1(三).以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:====﹣1(四);
请根据材料解答下列问题:
(1)= ;= .
(2)化简:+++…+.
参考答案
一.选择题
1.【解答】解:是二次根式的有、,共2个;
故选:B.
2.【解答】解:根据二次根式有意义的条件得:7﹣x≥0,
∴x≤7,
∴符合题意的是0,
故选:D.
3.【解答】解:∵=,
∴选项A不符合题意;
∵=2,
∴选项B不符合题意;
∵已是最简二次根式,
∴选项C符合题意;
∵=2,
∴选项D不符合题意;
故选:C.
4.【解答】解:A、=2与2不是同类二次根式,不能合并,故A不符合题意;
B、=2与2不是同类二次根式,不能合并,故B不符合题意;
C、=3与2是同类二次根式,能合并,故C符合题意;
D、与2不是同类二次根式,不能合并,故D不符合题意;
故选:C.
5.【解答】解:A.+无法合并,故此选项不合题意;
B.4﹣3=,故此选项不合题意;
C.﹣=,故此选项符合题意;
D.3+2无法合并,故此选项不合题意;
故选:C.
6.【解答】解:∵=a,=b,
∴==×=ab.
故选:C.
7.【解答】解:=2,
∵是整数,
∴n的最小值是5,
故选:D.
8.【解答】解:原式=[(+3)(﹣3)]2019(+3)
=(10﹣9)2019(+3)
=+3,
故选:D.
二.填空题
9.【解答】解:(﹣)2=3.
故答案为:3.
10.【解答】解:由题意得:4﹣2x≥0且x+1≠0,
解得:x≤2且x≠﹣1,
故答案为:x≤2且x≠﹣1.
11.【解答】解:设长方形的另外一边为x(cm),
∴x==6(cm),
∴周长为:2(6+)=20(cm),
故答案为:20(cm).
12.【解答】解:由数轴可得,a<0,b>0,a﹣b<0,
∴原式=|a|﹣|b|﹣|a﹣b|
=﹣a﹣b﹣(﹣a+b)
=﹣a﹣b+a﹣b
=﹣2b,
故答案为:﹣2b.
13.【解答】解:∵,,
∴x+y=2,x﹣y=2,
∴x2﹣y2
=(x+y)(x﹣y)
=2×2
=4,
故答案为:4.
14.【解答】解:∵3>2,8<12,
∴原式=(﹣)+(+)
=﹣+2+2
=3+,
故答案为:3+.
三.解答题
15.【解答】解:(1)原式=×
=.
(2)原式=
=5.
(3)原式=
=.
(4)原式=
=.
16.【解答】解:(1)原式=5﹣3+4
=5+.
(2)原式=6﹣2﹣(3﹣2+1)
=4﹣(4﹣2)
=4﹣4+2
=2.
17.【解答】解:原式=
=a﹣3,
当a=﹣1时,
原式=(﹣1)﹣3
=2﹣﹣3
=﹣1﹣.
18.【解答】解:∵三角形周长为,两边长为,
∴第三边长为:==(cm),
答:第三边长为2cm.
19.【解答】解:∵a=5+2,b=5﹣2,
∴a+b=10,ab=1,
(1)a2b+ab2
=ab(a+b)
=1×10
=10;
(2)(+)2
=a+b+2
=10+2×
=12,
∵+≥0,
∴+==2.
20.【解答】解:(1)∵3﹣2=2+1﹣2=(﹣1)2,
∴==﹣1,
∵4+2=3+1+2=(+1)2,
∴==+1,
故答案为:﹣1,+1;
(2)+++…+
=++ +
=﹣1+﹣+﹣+ +﹣
=﹣1+.
