人教版九年级数学下册第二十九章《投影与视图》知识讲解及考前预测卷精讲(第二套)+课件(36张PPT).pptx
文档属性
| 名称 | 人教版九年级数学下册第二十九章《投影与视图》知识讲解及考前预测卷精讲(第二套)+课件(36张PPT).pptx |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 09:10:59 | ||
图片预览










文档简介
(共36张PPT)
人教版九年级数学下册第二十九章
《投影与视图》知识讲解及考前预测卷精讲
(第二套)
专题复习课件
知识讲解
01
第一部分:知识讲解
29.1 投影
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影(projection),照射光线叫做投影线,投影所在的平面叫做投影面。
有时光线是一组互相平行的射线,例如太阳光或探照灯光的一束光中的光线。由平行光线形成的投影是平行投影(parallel projection).
由同一点(点光源发出的光线)形成的投影叫做中心投影(center projection)。投影线垂直于投影面产生的投影叫做正投影。
投影线平行于投影面产生的投影叫做平行投影。
物体正投影的形状、大小与它相对于投影面的位置有关。
第一部分:知识讲解
29.2 三视图
三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形。
将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用正投影法绘制出来该图形称为视图。一个物体有六个视图:从物体的前面向后面投射所得的视图称主视图——能反映物体的前面形状,从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状,从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状,
还有其它三个视图不是很常用。三视图就是主视图、俯视图、左视图的总称。
特点:一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
主视、俯视 长对正
主视、左视 高平齐
左视、俯视 宽相等
第一部分:知识讲解
考前押题卷精讲
(全解析)
02
第二部分:学习检测
05
01
02
03
选择题
填空题
解答题
讲解流程
一.选择题
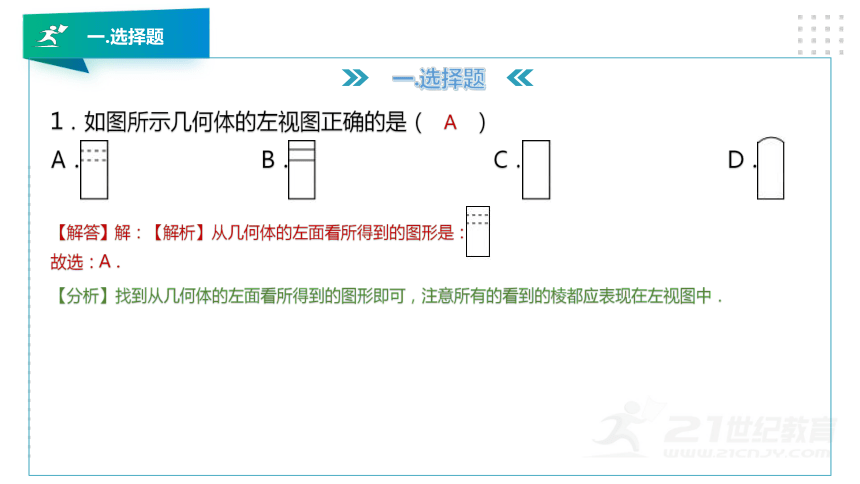
1.如图所示几何体的左视图正确的是( )
A. B. C. D.
【分析】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
A
一.选择题
【解答】解:【解析】从几何体的左面看所得到的图形是:
故选:A.
一.选择题
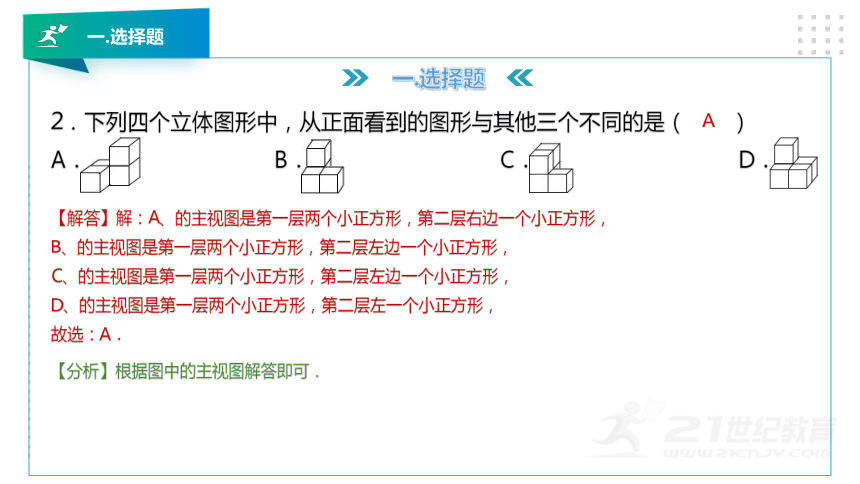
2.下列四个立体图形中,从正面看到的图形与其他三个不同的是( )
A. B. C. D.
【分析】根据图中的主视图解答即可.
A
一.选择题
【解答】解:A、的主视图是第一层两个小正方形,第二层右边一个小正方形,
B、的主视图是第一层两个小正方形,第二层左边一个小正方形,
C、的主视图是第一层两个小正方形,第二层左边一个小正方形,
D、的主视图是第一层两个小正方形,第二层左一个小正方形,
故选:A.
一.选择题
3.如图,这个圆锥的主(正)视图是一个边长为4的等边三角形,则这个圆锥的俯视图的面积为( )
A.4π B.8π C. D.
【分析】圆锥的俯视图是一个带圆心的圆,根据主(正)视图是一个边长为4的等边三角形可知,该圆半径为2,进而得出这个圆锥的俯视图的面积.
A
一.选择题
【解答】解:由题可得,圆锥的俯视图是一个带圆心的圆,
由圆锥的主(正)视图是一个边长为4的等边三角形可知,该圆半径为2,
故该圆的面积为4π.
故选:A.
一.选择题
4.桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图所示,则组成这个几何体的小正方体的个数最多有( )
A.12个 B.8个 C.14个 D.13个
【分析】易得此几何体有三行,三列,判断出各行各列最多有几个正方体组成即可.
D
一.选择题
【解答】解:底层正方体最多有9个正方体,第二层最多有4个正方体,所以组成这个几何体的小正方体的个数最多有13个.
故选:D.
一.选择题
5.如图,太阳光线AC和A′C′是平行的,在同一时刻,若两根木杆的影子一样长,则两根木杆高度相等.这利用了全等图形的性质,其中判断△ABC≌△A′B′C′的依据是( )
A.SAS B.AAS C.SSS D.ASA
【分析】根据平行线的性质可得∠ACB=∠A′C′B′,根据题意可得BC=B′C′,∠ABC=∠A′B′C′=90°,然后利用ASA判定△ABC≌△A′B′C′.
D
一.选择题
一.选择题
一.选择题
【解答】解:∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
∵两根木杆的影子一样长,
∴BC=B′C′,
在△ACB和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
故选:D.
一.选择题
6.将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是
( )
A. B. C. D.
【分析】找到从上面看所得到的图形即可,注意看见的棱用实线表示.
C
一.选择题
【解答】解:从上面看可得到一个正方形,正方形里面有一条撇向的实线.
故选:C.
一.选择题
7.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有( )
A.4个 B.8个 C.12个 D.17个
【分析】从俯视图中可以看出最底层碟子的个数及形状,从主视图可以看出每一层碟子的层数和个数,从而算出总的个数.
C
一.选择题
【解答】解:易得三摞碟子数从左往右分别为5,4,3,
则这个桌子上共有5+4+3=12个碟子
故答案:C
一.选择题
8.一个圆柱体钢块,正中央被挖去了一个长方体孔,其俯视图如图所示.则此圆柱体钢块的主视图可能是下列选项中的( )
A. B. C. D.
【分析】主视图是从物体正面看所得到的图形.几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线化成虚线.
C
一.选择题
【解答】解:此圆柱体钢块的主视图可能是:
故选:C.
一.选择题
9.把一个正六棱柱如图水平放置,一束水平方向的平行光线照射此正六棱柱时的正投影是( )
A. B. C. D.
【分析】根据平行投影特点以及图中正六棱柱的摆放位置即可求解.
B
一.选择题
【解答】解:把一个正六棱柱如图摆放,束水平方向的平行光线照射此正六棱柱时的正投影是矩形.
故选:B.
一.选择题
10.一个长方体的三视图及相应的棱长如图所示,则这个长方体的体积为( )
A.15 B.30 C.45 D.62
【分析】易得该长方体长为3,宽为3,高为5,根据长方体的体积=长×宽×高列式计算即可求解.
C
一.选择题
【解答】解:观察图形可知,该几何体为长3,宽3,高5的长方体,
长方体的体积为3×3×5=45.
故选:C.
二.填空题
11.如图是测得的两根木杆在同一时间的影子,那么它们是由________形成的投影(填“太阳光”或“灯光”).
【分析】根据平行投影与中心投影的定义即可判断.
太阳光
二.填空题
【解答】解:由投影中光线是平行的可知它们是由太阳光形成的投影,
故答案为:太阳光.
二.填空题
12.如图,是一个底面为直角三角形的直三棱柱的三视图,其表面积等____cm2.
【分析】由几何体的三视图可得出原几何体为直三棱柱,根据图中给定数据解答即可.
48
二.填空题
【解答】解:直三棱柱的表面积= ×3×4×2+3×4+3×3+3×5=48cm2.
故答案为:48.
二.填空题
13.一个由小立方块搭成的几何体,从正面、左面、上面看到的形状图如图所示,这个几何体是由_____个小立方块搭成的.
【分析】从俯视图中可以看出最底层小立方块的个数及形状,从主视图可以看出每一层小立方块的层数和个数,从左视图可看出每一行小立方块的层数和个数,从而算出总的个数.
5
二.填空题
【解答】解:由俯视图易得最底层小立方块的个数为4,由其他视图可知第二层有一个小立方块,那么共有4+1=5个小立方块.
故答案为:5.
二.填空题
14.如图是一个几何体的三视图,则这个几何体的侧面积是_____.
【分析】首先判断出该几何体是三棱柱,然后根据圆柱的侧面积公式计算这个几何体的侧面积即可.
36
二.填空题
【解答】解:观察三视图知:该几何体为三棱柱,高为3cm,长为4cm,
侧面积为:3×4×3=36cm2.
则这个几何体的侧面积是36cm2.
故答案为:36
二.填空题
15.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为_____m.
【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,进而可得 ;即DC2=ED FD,代入数据可得答案.
4
二.填空题
【解答】解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有 ;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
二.填空题
16.一块直角三角形板ABC,∠ACB=90°,BC=12cm,AC=8cm,测得BC边的中心投影B1C1长为24cm,则A1B1长为________cm.
【分析】由题意易得△ABC∽△A1B1C1,根据相似比求A1B1即可.
二.填空题
【解答】解:∵∠ACB=90°,BC=12cm,AC=8cm,
∴AB= ,∵△ABC∽△A1B1C1,
∴A1B1:AB=B1C1:BC=2:1,即A1B1= cm.
故答案:
二.填空题
17.已知一个几何体的三视图如图所示,则这个几何体的侧面积是______cm2.
【分析】由图可得底面三角形的三边都为3,正三棱柱的高为5,侧面积等于三个矩形的面积,根据长方形面积公式计算即可求解.
45
二.填空题
【解答】解:3×5×3=45(cm2).
故这个几何体的侧面积是45cm2.
故答案为:45.
二.填空题
18.老师用10个1cm×1cm×1cm的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边(1cm)共享,或有一面(1cm×1cm)共享.老师拿出一张3cm×4cm的方格纸(如图②),请小荣将此10个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有______种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
16
二.填空题
【解答】解:由题意可知,立体图形只有一排左视图有3个正方形,有两到三排.
三排的左视图有:3×4=12种;
两排的左视图有:2×2=4种;
共12+4=16种.
故答案为:16.
二.填空题
【分析】小荣摆放完后的左视图有:①从左往右依次是3个正方形、1个正方形、1个正方形;②从左往右依次是3个正方形、1个正方形、2个正方形;③从左往右依次是3个正方形、2个正方形、1个正方形;④从左往右依次是3个正方形、2个正方形、2个正方形;⑤从左往右依次是2个正方形、3个正方形、1个正方形;⑥从左往右依次是2个正方形、3个正方形、2个正方形;⑦从左往右依次是2个正方形、1个正方形、3个正方形;⑧从左往右依次是2个正方形、2个正方形、3个正方形;⑨从左往右依次是1个正方形、3个正方形、1个正方形;⑩从左往右依次是1个正方形、3个正方形、2个正方形;(11)从左往右依次是1个正方形、1个正方形、3个正方形;(12)从左往右依次是1个正方形、2个正方形、3个正方形;(13)从左往右依次是3个正方形、1个正方形;(14)从左往右依次是3个正方形、2个正方形; (15)从左往右依次是2个正方形、3个正方形;(16)从左往右依次是1个正方形、3个正方形;
二.填空题
三.解答题
19.画出如图由7个小立方块搭成的几何体的三视图.
【分析】从正面看到的是两行三列,其中第一行两个小正方形,第二行是三个小正方形,从左面看到的是两行两列,每行、列都是两个小正方形,从上面看到的形状与主视图的相同.
三.解答题
【解答】解:这个几何体的三视图如图所示:
三.解答题
20.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数.
(1)请画出这个几何体的主视图和左视图.
(2)若小正方体的棱长为1.求该几何体的体积.
【分析】(1)根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而得出答案;
(2)利用已知俯视图上所标小立方体的个数得出答案.
三.解答题
【解答】解:(1)如图所示:
(2)该几何体的体积为:10.
三.解答题
21.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫______(填“能”或“不能”)晒到太阳.
【参考数据:1.732】
【分析】(1)在Rt△ABE中,由tan60°= ,即可求出AB的长;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
三.解答题
能
【解答】解:(1)当α=60°时,在Rt△ABE中,
∵tan60°= ,
∴AB=10 tan60°= ≈10×1.73=17.3(米).
即楼房的高度约为17.3米;
(2)当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,
∴tan45°= =1,此时的影长AF=AB=17.3米,
∴CF=AF﹣AC=17.3﹣17.2=0.1米,
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫能晒到太阳.
故答案为:能.
三.解答题
三.解答题
三.解答题
22.如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
【分析】(1)首先连接GA、HC并延长交于点O,从而确定点光源,然后连接OE并延长即可确定影子;
(2)OM⊥QH 设OM=x,BM=y,根据三角形相似列出比例式即可确定灯的高度.
三.解答题
【解答】解:(1)点O为灯的位置,QF为丙物体的影子;
(2)作OM⊥QH 设OM=x,BM=y,
由△GAB∽△GOM得
即: ①,
由△CDH∽△OMH得
即: ②
由①②得,
x=4.8,y=0.6.
答灯的高度为4.8米.
三.解答题
23.如图,小欣站在灯光下,投在地面上的身影AB=2.4m,蹲下来,则身影AC=1.05m,已知小欣的身高AD=1.6m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
【分析】利用平行线分线段成比例定理,构建方程组即可解决问题.
三.解答题
【解答】解:因为AD∥PH,
∴△ADB∽△HPB;△AMC∽△HPC(M是AD的中点),
∴AB:HB=AD:PH,AC:AM=HC:PH,
即2.4:(2.4+AH)=1.6:PH,1.05:0.8=(1.05+HA):PH,
解得:PH=7.2m.
即路灯的高度为7.2米.
三.解答题
24.如图,是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看长方形的高为9cm,从上面看三角形的边长都为5cm,求这个几何体的侧面积.
【分析】(1)根据三视图,即可解决问题;
(2)画出正三棱柱的侧面展开图即可;
(3)侧面展开图是矩形,求出矩形的面积即可.
三.解答题
【解答】解:(1)这个几何体的名称是正三棱柱;
(2)表面展开图如下(答案不唯一):
(3)S侧=3×5×9=15×9=135(cm2).
答:这个几何体的侧面积是135cm2.
谢谢您的观看!
https://www.21cnjy.com/help/help_extract.php
人教版九年级数学下册第二十九章
《投影与视图》知识讲解及考前预测卷精讲
(第二套)
专题复习课件
知识讲解
01
第一部分:知识讲解
29.1 投影
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影(projection),照射光线叫做投影线,投影所在的平面叫做投影面。
有时光线是一组互相平行的射线,例如太阳光或探照灯光的一束光中的光线。由平行光线形成的投影是平行投影(parallel projection).
由同一点(点光源发出的光线)形成的投影叫做中心投影(center projection)。投影线垂直于投影面产生的投影叫做正投影。
投影线平行于投影面产生的投影叫做平行投影。
物体正投影的形状、大小与它相对于投影面的位置有关。
第一部分:知识讲解
29.2 三视图
三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形。
将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用正投影法绘制出来该图形称为视图。一个物体有六个视图:从物体的前面向后面投射所得的视图称主视图——能反映物体的前面形状,从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状,从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状,
还有其它三个视图不是很常用。三视图就是主视图、俯视图、左视图的总称。
特点:一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
主视、俯视 长对正
主视、左视 高平齐
左视、俯视 宽相等
第一部分:知识讲解
考前押题卷精讲
(全解析)
02
第二部分:学习检测
05
01
02
03
选择题
填空题
解答题
讲解流程
一.选择题
1.如图所示几何体的左视图正确的是( )
A. B. C. D.
【分析】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
A
一.选择题
【解答】解:【解析】从几何体的左面看所得到的图形是:
故选:A.
一.选择题
2.下列四个立体图形中,从正面看到的图形与其他三个不同的是( )
A. B. C. D.
【分析】根据图中的主视图解答即可.
A
一.选择题
【解答】解:A、的主视图是第一层两个小正方形,第二层右边一个小正方形,
B、的主视图是第一层两个小正方形,第二层左边一个小正方形,
C、的主视图是第一层两个小正方形,第二层左边一个小正方形,
D、的主视图是第一层两个小正方形,第二层左一个小正方形,
故选:A.
一.选择题
3.如图,这个圆锥的主(正)视图是一个边长为4的等边三角形,则这个圆锥的俯视图的面积为( )
A.4π B.8π C. D.
【分析】圆锥的俯视图是一个带圆心的圆,根据主(正)视图是一个边长为4的等边三角形可知,该圆半径为2,进而得出这个圆锥的俯视图的面积.
A
一.选择题
【解答】解:由题可得,圆锥的俯视图是一个带圆心的圆,
由圆锥的主(正)视图是一个边长为4的等边三角形可知,该圆半径为2,
故该圆的面积为4π.
故选:A.
一.选择题
4.桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图所示,则组成这个几何体的小正方体的个数最多有( )
A.12个 B.8个 C.14个 D.13个
【分析】易得此几何体有三行,三列,判断出各行各列最多有几个正方体组成即可.
D
一.选择题
【解答】解:底层正方体最多有9个正方体,第二层最多有4个正方体,所以组成这个几何体的小正方体的个数最多有13个.
故选:D.
一.选择题
5.如图,太阳光线AC和A′C′是平行的,在同一时刻,若两根木杆的影子一样长,则两根木杆高度相等.这利用了全等图形的性质,其中判断△ABC≌△A′B′C′的依据是( )
A.SAS B.AAS C.SSS D.ASA
【分析】根据平行线的性质可得∠ACB=∠A′C′B′,根据题意可得BC=B′C′,∠ABC=∠A′B′C′=90°,然后利用ASA判定△ABC≌△A′B′C′.
D
一.选择题
一.选择题
一.选择题
【解答】解:∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
∵两根木杆的影子一样长,
∴BC=B′C′,
在△ACB和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
故选:D.
一.选择题
6.将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是
( )
A. B. C. D.
【分析】找到从上面看所得到的图形即可,注意看见的棱用实线表示.
C
一.选择题
【解答】解:从上面看可得到一个正方形,正方形里面有一条撇向的实线.
故选:C.
一.选择题
7.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有( )
A.4个 B.8个 C.12个 D.17个
【分析】从俯视图中可以看出最底层碟子的个数及形状,从主视图可以看出每一层碟子的层数和个数,从而算出总的个数.
C
一.选择题
【解答】解:易得三摞碟子数从左往右分别为5,4,3,
则这个桌子上共有5+4+3=12个碟子
故答案:C
一.选择题
8.一个圆柱体钢块,正中央被挖去了一个长方体孔,其俯视图如图所示.则此圆柱体钢块的主视图可能是下列选项中的( )
A. B. C. D.
【分析】主视图是从物体正面看所得到的图形.几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线化成虚线.
C
一.选择题
【解答】解:此圆柱体钢块的主视图可能是:
故选:C.
一.选择题
9.把一个正六棱柱如图水平放置,一束水平方向的平行光线照射此正六棱柱时的正投影是( )
A. B. C. D.
【分析】根据平行投影特点以及图中正六棱柱的摆放位置即可求解.
B
一.选择题
【解答】解:把一个正六棱柱如图摆放,束水平方向的平行光线照射此正六棱柱时的正投影是矩形.
故选:B.
一.选择题
10.一个长方体的三视图及相应的棱长如图所示,则这个长方体的体积为( )
A.15 B.30 C.45 D.62
【分析】易得该长方体长为3,宽为3,高为5,根据长方体的体积=长×宽×高列式计算即可求解.
C
一.选择题
【解答】解:观察图形可知,该几何体为长3,宽3,高5的长方体,
长方体的体积为3×3×5=45.
故选:C.
二.填空题
11.如图是测得的两根木杆在同一时间的影子,那么它们是由________形成的投影(填“太阳光”或“灯光”).
【分析】根据平行投影与中心投影的定义即可判断.
太阳光
二.填空题
【解答】解:由投影中光线是平行的可知它们是由太阳光形成的投影,
故答案为:太阳光.
二.填空题
12.如图,是一个底面为直角三角形的直三棱柱的三视图,其表面积等____cm2.
【分析】由几何体的三视图可得出原几何体为直三棱柱,根据图中给定数据解答即可.
48
二.填空题
【解答】解:直三棱柱的表面积= ×3×4×2+3×4+3×3+3×5=48cm2.
故答案为:48.
二.填空题
13.一个由小立方块搭成的几何体,从正面、左面、上面看到的形状图如图所示,这个几何体是由_____个小立方块搭成的.
【分析】从俯视图中可以看出最底层小立方块的个数及形状,从主视图可以看出每一层小立方块的层数和个数,从左视图可看出每一行小立方块的层数和个数,从而算出总的个数.
5
二.填空题
【解答】解:由俯视图易得最底层小立方块的个数为4,由其他视图可知第二层有一个小立方块,那么共有4+1=5个小立方块.
故答案为:5.
二.填空题
14.如图是一个几何体的三视图,则这个几何体的侧面积是_____.
【分析】首先判断出该几何体是三棱柱,然后根据圆柱的侧面积公式计算这个几何体的侧面积即可.
36
二.填空题
【解答】解:观察三视图知:该几何体为三棱柱,高为3cm,长为4cm,
侧面积为:3×4×3=36cm2.
则这个几何体的侧面积是36cm2.
故答案为:36
二.填空题
15.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为_____m.
【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,进而可得 ;即DC2=ED FD,代入数据可得答案.
4
二.填空题
【解答】解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有 ;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
二.填空题
16.一块直角三角形板ABC,∠ACB=90°,BC=12cm,AC=8cm,测得BC边的中心投影B1C1长为24cm,则A1B1长为________cm.
【分析】由题意易得△ABC∽△A1B1C1,根据相似比求A1B1即可.
二.填空题
【解答】解:∵∠ACB=90°,BC=12cm,AC=8cm,
∴AB= ,∵△ABC∽△A1B1C1,
∴A1B1:AB=B1C1:BC=2:1,即A1B1= cm.
故答案:
二.填空题
17.已知一个几何体的三视图如图所示,则这个几何体的侧面积是______cm2.
【分析】由图可得底面三角形的三边都为3,正三棱柱的高为5,侧面积等于三个矩形的面积,根据长方形面积公式计算即可求解.
45
二.填空题
【解答】解:3×5×3=45(cm2).
故这个几何体的侧面积是45cm2.
故答案为:45.
二.填空题
18.老师用10个1cm×1cm×1cm的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边(1cm)共享,或有一面(1cm×1cm)共享.老师拿出一张3cm×4cm的方格纸(如图②),请小荣将此10个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有______种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
16
二.填空题
【解答】解:由题意可知,立体图形只有一排左视图有3个正方形,有两到三排.
三排的左视图有:3×4=12种;
两排的左视图有:2×2=4种;
共12+4=16种.
故答案为:16.
二.填空题
【分析】小荣摆放完后的左视图有:①从左往右依次是3个正方形、1个正方形、1个正方形;②从左往右依次是3个正方形、1个正方形、2个正方形;③从左往右依次是3个正方形、2个正方形、1个正方形;④从左往右依次是3个正方形、2个正方形、2个正方形;⑤从左往右依次是2个正方形、3个正方形、1个正方形;⑥从左往右依次是2个正方形、3个正方形、2个正方形;⑦从左往右依次是2个正方形、1个正方形、3个正方形;⑧从左往右依次是2个正方形、2个正方形、3个正方形;⑨从左往右依次是1个正方形、3个正方形、1个正方形;⑩从左往右依次是1个正方形、3个正方形、2个正方形;(11)从左往右依次是1个正方形、1个正方形、3个正方形;(12)从左往右依次是1个正方形、2个正方形、3个正方形;(13)从左往右依次是3个正方形、1个正方形;(14)从左往右依次是3个正方形、2个正方形; (15)从左往右依次是2个正方形、3个正方形;(16)从左往右依次是1个正方形、3个正方形;
二.填空题
三.解答题
19.画出如图由7个小立方块搭成的几何体的三视图.
【分析】从正面看到的是两行三列,其中第一行两个小正方形,第二行是三个小正方形,从左面看到的是两行两列,每行、列都是两个小正方形,从上面看到的形状与主视图的相同.
三.解答题
【解答】解:这个几何体的三视图如图所示:
三.解答题
20.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数.
(1)请画出这个几何体的主视图和左视图.
(2)若小正方体的棱长为1.求该几何体的体积.
【分析】(1)根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而得出答案;
(2)利用已知俯视图上所标小立方体的个数得出答案.
三.解答题
【解答】解:(1)如图所示:
(2)该几何体的体积为:10.
三.解答题
21.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫______(填“能”或“不能”)晒到太阳.
【参考数据:1.732】
【分析】(1)在Rt△ABE中,由tan60°= ,即可求出AB的长;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
三.解答题
能
【解答】解:(1)当α=60°时,在Rt△ABE中,
∵tan60°= ,
∴AB=10 tan60°= ≈10×1.73=17.3(米).
即楼房的高度约为17.3米;
(2)当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,
∴tan45°= =1,此时的影长AF=AB=17.3米,
∴CF=AF﹣AC=17.3﹣17.2=0.1米,
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫能晒到太阳.
故答案为:能.
三.解答题
三.解答题
三.解答题
22.如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
【分析】(1)首先连接GA、HC并延长交于点O,从而确定点光源,然后连接OE并延长即可确定影子;
(2)OM⊥QH 设OM=x,BM=y,根据三角形相似列出比例式即可确定灯的高度.
三.解答题
【解答】解:(1)点O为灯的位置,QF为丙物体的影子;
(2)作OM⊥QH 设OM=x,BM=y,
由△GAB∽△GOM得
即: ①,
由△CDH∽△OMH得
即: ②
由①②得,
x=4.8,y=0.6.
答灯的高度为4.8米.
三.解答题
23.如图,小欣站在灯光下,投在地面上的身影AB=2.4m,蹲下来,则身影AC=1.05m,已知小欣的身高AD=1.6m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
【分析】利用平行线分线段成比例定理,构建方程组即可解决问题.
三.解答题
【解答】解:因为AD∥PH,
∴△ADB∽△HPB;△AMC∽△HPC(M是AD的中点),
∴AB:HB=AD:PH,AC:AM=HC:PH,
即2.4:(2.4+AH)=1.6:PH,1.05:0.8=(1.05+HA):PH,
解得:PH=7.2m.
即路灯的高度为7.2米.
三.解答题
24.如图,是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看长方形的高为9cm,从上面看三角形的边长都为5cm,求这个几何体的侧面积.
【分析】(1)根据三视图,即可解决问题;
(2)画出正三棱柱的侧面展开图即可;
(3)侧面展开图是矩形,求出矩形的面积即可.
三.解答题
【解答】解:(1)这个几何体的名称是正三棱柱;
(2)表面展开图如下(答案不唯一):
(3)S侧=3×5×9=15×9=135(cm2).
答:这个几何体的侧面积是135cm2.
谢谢您的观看!
https://www.21cnjy.com/help/help_extract.php
