湖南师大附属颐华高级中学(平江)有限公司2021-2022学年高二学业水平测试模拟试卷(Word版含答案)
文档属性
| 名称 | 湖南师大附属颐华高级中学(平江)有限公司2021-2022学年高二学业水平测试模拟试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 432.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 06:54:57 | ||
图片预览



文档简介
湖南师大附属颐华学校2021-2022学年第二学期
学业水平测试模拟试卷(一)
一、选择题
1.已知集合( )
A. B. C. D.
2.设命题存在则 为( )
A.存在 B. 不存在 C.对任意 D. 对任意
3.设集合,则下列关系式正确的是( )
A. B. C. D.
4.已知,则( )
A. B. C. D.
5.已知向量且,则( )
A.3 B.-3 C. D.
6.对于直线,以及平面,下列说法中正确的是( )
A.如果,则 B.如果,则
C. 如果,则 D.如果,则
7.函数是( )
A.周期为的奇函数 B.周期为的偶函数
C. 周期为的奇函数 D.周期为的偶函数
8.一个正三角形的外接圆的半径为1,向该圆内随机投一点P,点P恰好落在正三角形内的概率是( )
A. B. C. D.
9.某校共有学生2000名,各年级男、女学生人数如表,现用分层抽样的方法在全校学生中抽取64人,则应在三年级抽取的学生人数为( )
一年级 二年级 三年级
女生 385 380 b
男生 375 360 c
A.19 B.16 C.500 D.18
10.下列式子不正确的是( )
A. B.
C. D.
二、填空题
11.已知,点O在二面角的棱上,点P在平面内,且.若直线PO与平面所成的角为45°,则二面角的正弦值为_________________.
12.已知圆锥的底面半径、高、体积分别为2、3、,圆柱的底面半径、高、体积分别为1、,则 ,圆锥的外接球的表面积为 .
13.若,则的最小值为__________
14.如果二次函数存在零点,则的取值范围是___________
15.已知的三个内角所对的边分别为,,则边____________
三、解答题
16.已知的内角的对边分别为,
(1)求角的大小;
(2)若的面积为,周长为,求的值。
17.如图,在圆柱 中,是圆柱的母线,是圆柱的底面的直径,D是底面圆周上异于的点.
(1)求证: 平面;
(2)若,,,求圆柱的侧面积.
18.如图所示,为函数图像的一部分.根据图像:
1.求出函数的解析式;
2.写出的单调递增区间.
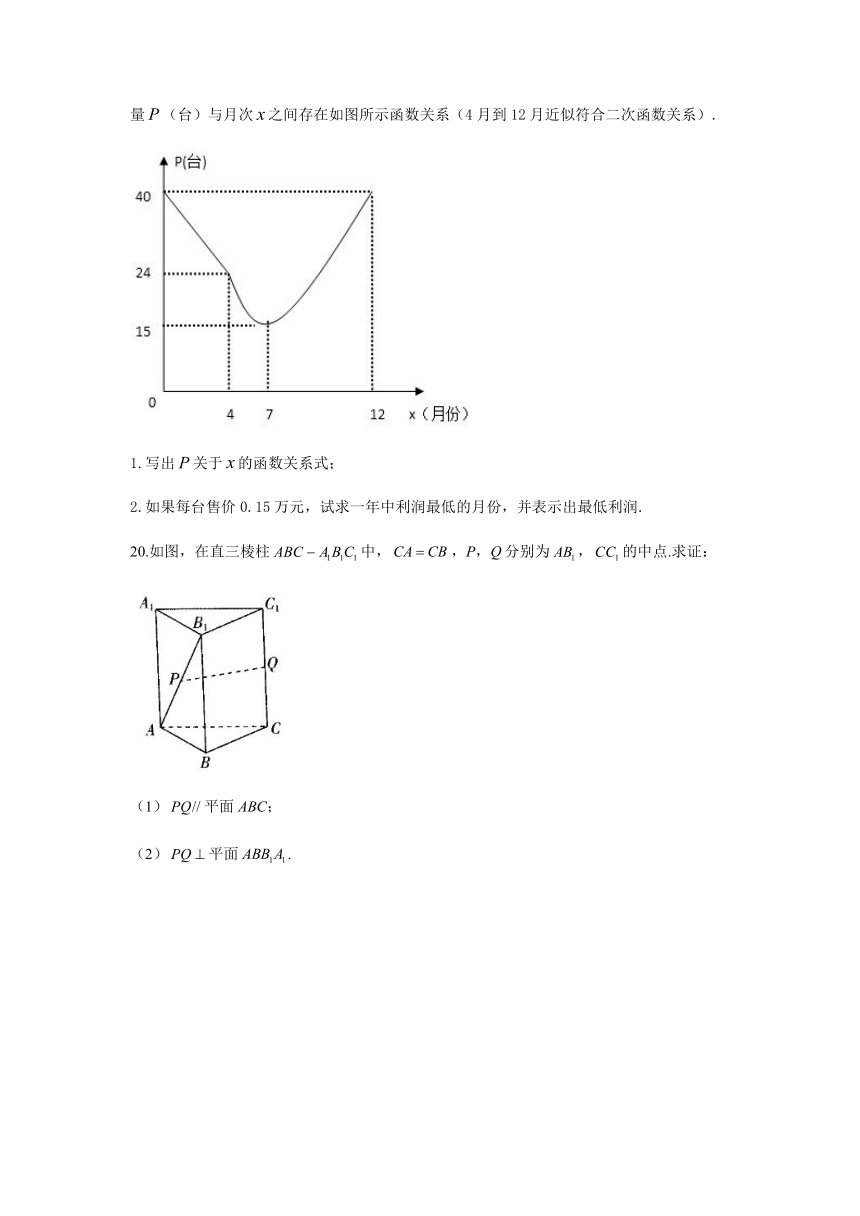
19.由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖。某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量(台)与月次之间存在如图所示函数关系(4月到12月近似符合二次函数关系).
1.写出关于的函数关系式;
2.如果每台售价0.15万元,试求一年中利润最低的月份,并表示出最低利润.
20.如图,在直三棱柱中,,P,Q分别为,的中点.求证:
(1)平面ABC;
(2)平面.
参考答案
1.答案:B
2.答案:C
3.答案:C
4.答案:B
5.答案:A
6.答案:D
7.答案:C
8.答案:A
9.答案:B
10.答案:D
11.答案:
解析:如图,过点P作,垂足为E,过E作,垂足为F,连接OE,PF,则为直线PO与平面所成的角,为二面角的平面角.设,则在中,由,可得.在中,由,可得.在中,,即二面角的正弦值为.
12.答案:4,
解析:本题考查圆锥、圆柱的体积以及圆锥的外接球问题。依题有。
设圆锥的外接球的半径为,则有,解得,
则圆锥的外接球的表面积为
13.答案:
14.答案:
15.答案:
16.答案:(1)因为,所以,
因为,所以,所以
(2)因为,所以
又因为,,所以,解得或(舍),故
17.答案: (1)证明见解析
(2)
解析: (1)由已知可知平面,平面,
点是上异于的点,是的直径,
所以,
又,∴ 平面
(2)在中,,,,
,
圆柱的侧面积为:.
18.答案:1.
,
当时,
2.,
的单调递增区间是
解析:
19.答案:1.从年初到4月函数关系为一次函数,经过点和
所以,此时的解析式为
从4月到12月函数关系为二次函数,顶点,经过点
设代入则
所以的解析式为:
2.从图像中可知,一年中的7月销售量最低,此时的利润也就最低。
此时的利润(万元)
解析:
20.答案:解析:(1)取AB的中点D,连接PD,CD.
在中,因为P,D分别为,AB的中点,
所以,.
在直三棱柱中,,.
因为Q为棱的中点,所以,且.
所以,且,
所以四边形PDCQ为平行四边形,从而.
又因为平面ABC,平面ABC,
所以平面ABC.
(2)在直三棱柱中,平面ABC.
因为平面ABC,所以.
在三角形ABC中,,D为AB的中点,所以.
因为,平面,平面,
所以平面.
又由(1)知,所以平面.
学业水平测试模拟试卷(一)
一、选择题
1.已知集合( )
A. B. C. D.
2.设命题存在则 为( )
A.存在 B. 不存在 C.对任意 D. 对任意
3.设集合,则下列关系式正确的是( )
A. B. C. D.
4.已知,则( )
A. B. C. D.
5.已知向量且,则( )
A.3 B.-3 C. D.
6.对于直线,以及平面,下列说法中正确的是( )
A.如果,则 B.如果,则
C. 如果,则 D.如果,则
7.函数是( )
A.周期为的奇函数 B.周期为的偶函数
C. 周期为的奇函数 D.周期为的偶函数
8.一个正三角形的外接圆的半径为1,向该圆内随机投一点P,点P恰好落在正三角形内的概率是( )
A. B. C. D.
9.某校共有学生2000名,各年级男、女学生人数如表,现用分层抽样的方法在全校学生中抽取64人,则应在三年级抽取的学生人数为( )
一年级 二年级 三年级
女生 385 380 b
男生 375 360 c
A.19 B.16 C.500 D.18
10.下列式子不正确的是( )
A. B.
C. D.
二、填空题
11.已知,点O在二面角的棱上,点P在平面内,且.若直线PO与平面所成的角为45°,则二面角的正弦值为_________________.
12.已知圆锥的底面半径、高、体积分别为2、3、,圆柱的底面半径、高、体积分别为1、,则 ,圆锥的外接球的表面积为 .
13.若,则的最小值为__________
14.如果二次函数存在零点,则的取值范围是___________
15.已知的三个内角所对的边分别为,,则边____________
三、解答题
16.已知的内角的对边分别为,
(1)求角的大小;
(2)若的面积为,周长为,求的值。
17.如图,在圆柱 中,是圆柱的母线,是圆柱的底面的直径,D是底面圆周上异于的点.
(1)求证: 平面;
(2)若,,,求圆柱的侧面积.
18.如图所示,为函数图像的一部分.根据图像:
1.求出函数的解析式;
2.写出的单调递增区间.
19.由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖。某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量(台)与月次之间存在如图所示函数关系(4月到12月近似符合二次函数关系).
1.写出关于的函数关系式;
2.如果每台售价0.15万元,试求一年中利润最低的月份,并表示出最低利润.
20.如图,在直三棱柱中,,P,Q分别为,的中点.求证:
(1)平面ABC;
(2)平面.
参考答案
1.答案:B
2.答案:C
3.答案:C
4.答案:B
5.答案:A
6.答案:D
7.答案:C
8.答案:A
9.答案:B
10.答案:D
11.答案:
解析:如图,过点P作,垂足为E,过E作,垂足为F,连接OE,PF,则为直线PO与平面所成的角,为二面角的平面角.设,则在中,由,可得.在中,由,可得.在中,,即二面角的正弦值为.
12.答案:4,
解析:本题考查圆锥、圆柱的体积以及圆锥的外接球问题。依题有。
设圆锥的外接球的半径为,则有,解得,
则圆锥的外接球的表面积为
13.答案:
14.答案:
15.答案:
16.答案:(1)因为,所以,
因为,所以,所以
(2)因为,所以
又因为,,所以,解得或(舍),故
17.答案: (1)证明见解析
(2)
解析: (1)由已知可知平面,平面,
点是上异于的点,是的直径,
所以,
又,∴ 平面
(2)在中,,,,
,
圆柱的侧面积为:.
18.答案:1.
,
当时,
2.,
的单调递增区间是
解析:
19.答案:1.从年初到4月函数关系为一次函数,经过点和
所以,此时的解析式为
从4月到12月函数关系为二次函数,顶点,经过点
设代入则
所以的解析式为:
2.从图像中可知,一年中的7月销售量最低,此时的利润也就最低。
此时的利润(万元)
解析:
20.答案:解析:(1)取AB的中点D,连接PD,CD.
在中,因为P,D分别为,AB的中点,
所以,.
在直三棱柱中,,.
因为Q为棱的中点,所以,且.
所以,且,
所以四边形PDCQ为平行四边形,从而.
又因为平面ABC,平面ABC,
所以平面ABC.
(2)在直三棱柱中,平面ABC.
因为平面ABC,所以.
在三角形ABC中,,D为AB的中点,所以.
因为,平面,平面,
所以平面.
又由(1)知,所以平面.
同课章节目录
