华师大版七年级下册第9章《多边形》全章导学案
文档属性
| 名称 | 华师大版七年级下册第9章《多边形》全章导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 24.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-09 12:17:17 | ||
图片预览



文档简介
导学案 9.1 三角形
1.认识三角形 第一课时
学习目标:
了解三角形及三角形的顶点、边、内角、外交等概念
了解三角形按角进行分类
了解等腰三角行、等边三角形(正三角形)
二、学习重点:
1、了解三角形及三角形的顶点、边、内角、外交等概念
2、了解三角形按角进行分类
3、了解等腰三角行、等边三角形(正三角形)
自学指导1:
认真看书本P55,并回答下面问题:
三角形的定义是什么?(用笔画在书上)
如图所示:
①整个三角形可以表示为______________
②三角形有___条边,分别可以表示为_____________________
③三角形有___个顶点,分别可以表示为____________________
④三角形的内角和为_________度
⑤三角形有_____个内角,分别可以表示为________________
⑥什么叫三角形的外角?(用笔画在书上)
⑦一个三角形一共有____个外角
⑧如图所示:请你做出的外角,一共能做出几个?它们有什么样的关系?
自学测试1:
指出图中有几个三角形?并把它们表示出来
指出△ADC的三个内角,三条边,并表示出来
CD是哪两个三角形的公共边?
是△BCD的什么角?是△ACD的什么角?是△ADC的外角吗?
画出相邻的外角
自学指导2:看书本P55-P56的试一试,并回答问题:
三角形按角分类可以分为三种:
_____________ ( )
_____________ ( )
_____________ ( )
三角形按边分类可以分为两种:
_____________
_______________
_____________
_______________
六、自学测试2:
完成书本P56的做一做和练习
导学案9.1 三角形
1.认识三角形 第二课时
学习目标:
1、了解三角形的中线、角平分线、高的概念
2、会画出任意三角形的角平分线、中线和高
3、会利用三角形内角和进行简单的计算
二、学习重点:
三角形中线、角平分线、高的画法
自学指导:
看书本P57的第一段,完成下面几个内容:
什么是三角形的中线?一个三角形有几条中线?完成做一做中的第一个作图。
什么是三角形的角平分线?它和角的平分线有区别吗?一个三角形有几条角平分线?完成做一做中的第二个作图。
什么是三角形的高?锐角三角形、直角三角形和钝角三角形的高画法一样吗?完成做一做中的第三个作图。并画出直角三角形和钝角三角形的三条高
完成P57的做一做中的填空题
自学测试:P57的练习
加强训练:
已知△ABC中,∠A:∠B:∠C=1:2:3,求△ABC各角的度数
已知:AC⊥BC,且∠A=60度,BD是△ABC的一条角平分线,
求:∠ABD的度数。
导学案9.1 三角形内角和与外角和
学习目标:
了解三角形的外角与内角的两条性质
了解三角形的外角和等于360度
会运用三角形内、外角的性质进行简单的计算和初步的说理
二、学习重点:
三角形外角的性质及三角形的外角和
自学指导:
三角形的内角和是多少?
认真阅读书本P57的内容,并完成以下几个问题:
完成P58的做一做
右图所示:
①外角有哪几个?__________________
②内角有哪几个?__________________
③与∠4相邻的内角是_________
④与∠4不相邻的内角是_________
⑤∠1+∠4=________
∠1+______+______=180
从上面两个式子可以发现:_____=_______+_______
即:三角形的外角性质1:___________________________________________
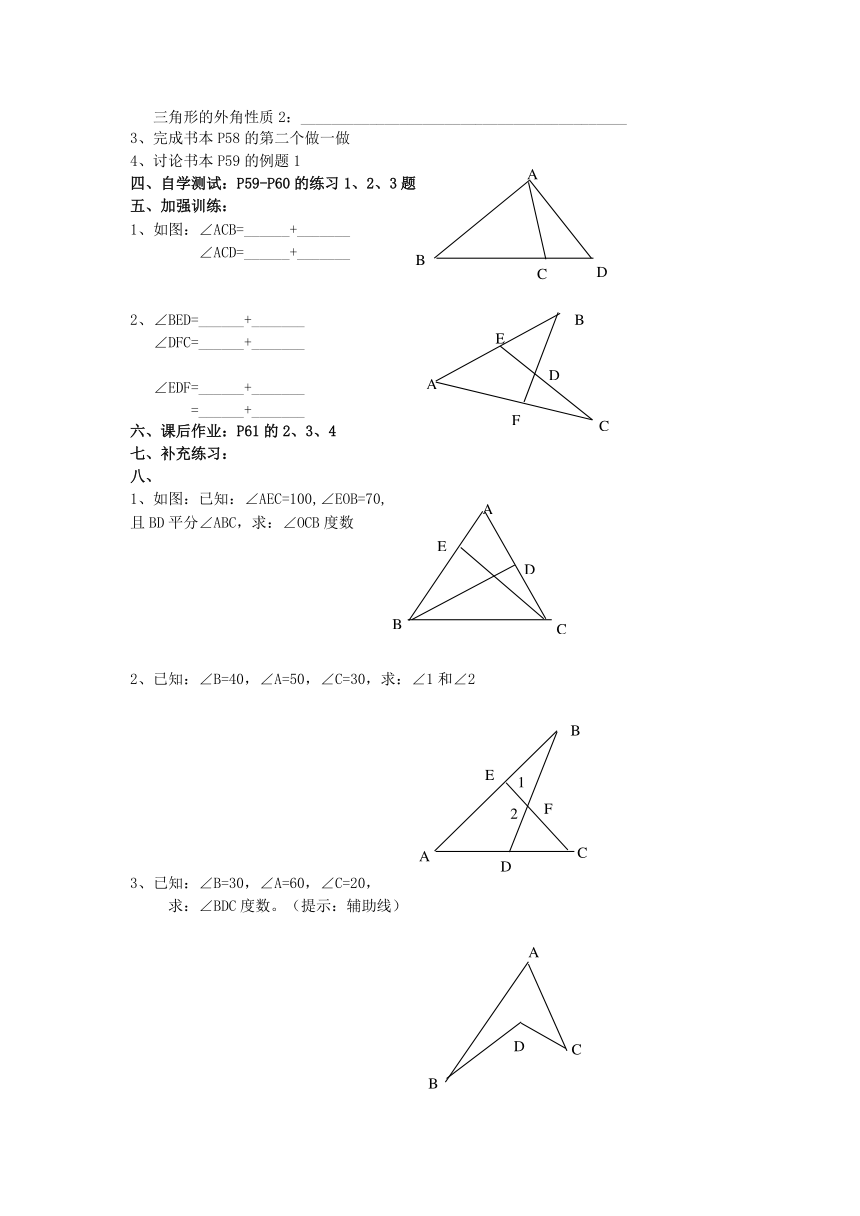
三角形的外角性质2:___________________________________________
完成书本P58的第二个做一做
讨论书本P59的例题1
自学测试:P59-P60的练习1、2、3题
加强训练:
1、如图:∠ACB=______+_______
∠ACD=______+_______
2、∠BED=______+_______
∠DFC=______+_______
∠EDF=______+_______
=______+_______
课后作业:P61的2、3、4
补充练习:
如图:已知:∠AEC=100,∠EOB=70,
且BD平分∠ABC,求:∠OCB度数
已知:∠B=40,∠A=50,∠C=30,求:∠1和∠2
3、已知:∠B=30,∠A=60,∠C=20,
求:∠BDC度数。(提示:辅助线)
4、已知:∠A=∠D+∠C
证明:EA∥FD
导学案9.1 三角形
3.三角形的三边关系
学习目标:
了解构成三角心的条件
知道三角形三边的关系
了解三角形的稳定性
二、学习重点:
三角形三边关系及其简单应用
自学指导:
复习提问:(1)三角形的内角和是多少?三角形的外角和是多少?三角形的外角有什么性质?
(2)如图所示,从A到B,走那一条路最短,
根据的数学原理是什么?
认真阅读书本P60的做一做下面那段话,
并完成做一做,画出三角形。
完成试一试,并讨论什么样的三条线段可以组成一个三角形。
阅读书本P60-P61的后面两段话,理解三角形具有_______性。
在生活中应用的例子有___________和__________,你还可以举出例子吗?
自学测试:P61的练习
加强训练:
下面不可以构成三角形的线段是哪一组( )
A、3,4,6 B、4,6,6 C、4,4,2 D、4,1,3
2、从2,3,6,4中任选三条线段组成一个三角形,
你可以选择哪三条?______________(写出一组即可)
3、木匠在安装木门的时候在门上固定一个木块,这是利用三角形的_____
4、一个三角形的三边分别是2,4,x,则x应满足什么取值范围________,若x为偶数,则x=______
5、已知等腰三角形的其中两条边分别为4和6,则第三条边为______
6、已知等腰三角形的其中两条边分别为2和6,则周长为______
7、已知一个等腰三角形的周长为24cm,其中一条边长为6,则
另外两边长分别为_____________
六、课后作业:P61的1,2,3,4
导学案9.2 多边形的内角和与外角和
第一课时
学习目标:
了解多边形的内角和
了解正多边形的概念
会运用多边形的内角和公式进行简单的计算
二、学习重点:
多边形的内角和公式及其应用
自学指导:
认真阅读书本P62-P63的内容,并回答下面问题:
完成P62中的试一试:说出什么叫四边形,什么叫五边形?
什么叫n边形?又称为什么?
你能区分凸多边形和凹多边形吗?
五边形和六边形分别有多少个内角?多少个外角?n边形呢?
什么叫正多边形?
什么是多边形的对角线?从四边形的一个顶点出发,可以画几条对角线呢?五边形和六边形呢?n边形呢?
将P63的图9.2.3中的三个图形的对角线全部画出来。
完成P63的探索中的表格,并写出n边形的内角和公式。
讨论完成P64的试一试,你能否用这种方法证明出多边形的内角和公式。
自学测试:认真阅读P64的例题,并完成下面题目
1、从六边形的一个顶点出发的对角线有____条,这些对角线将六边形分成_______个三角形
2、十边形的内角和度数是_________
3、一个多边形内角和度数是720度,那么这个多边形是_____边形
4、若一个多边形的每个内角度数都是120度,那么这是一个_____边形.
5、正六边形的每个内角度数都是_____度
五、课后作业:P65的1,2,3
导学案9.2 多边形的内角和与外角和
第二课时
学习目标:
了解多边形的外角和公式
了解从三角形到n边形,从外角到内角的“化归思想”
二、学习重点:
n边形外角和公式及其应用
自学指导:
多边形的内角和公式是________________
三角形的外角和是_________
认真阅读书本P64的第二段话,并完成探索中的表格
自学测试:完成书本P64的练习1,2
加强训练:
五边形的内角和是_____,外角和是______
八边形的外角和比七边形的外角和大,对吗?( )
一个多边形的每个外角都等于60度,这是一个______边形
一个多边形的每个内角都等于120度,这是一个_____边形
一个多边形的每个内角是外角的5倍,则这是一个_____边形
一个多边形的每个内角比外角多120度,则这是一个______边形
一个多边形的内角和是外角和的2倍,则这是一个____边形
补充练习:
1、正六边形的内角和是____,外角和是_____,每个外角等于____度,每个内角等于______度
2、多边形的边每增加一条边,内角和增加___度,外角和增加___度
3、一个多边形的每个外角都等于40度,这是一个______边形
4、一个多边形的每个内角都等于140度,这是一个_____边形
5、一个多边形的每个内角是外角的3倍,则这是一个_____边形
6、一个多边形的每个内角比外角多100度,则这是一个______边形
7、一个多边形的外角和是内角和的,则这是一个____边形
六、课后作业:P70的5,6,7,8,9
导学案9.3 用正多边形拼地板
用相同的正多边形拼地板
学习目标:
知道正三角形、正方形或正六边形可以镶嵌平面
知道拼成一个不留空隙又不重叠的平面图形的关键是n个多边形的内角和相加等于
二、学习重点:
用相同的正多边形“拼地板”
自学指导:
复习:(1)多边形的内角和公式是________,外角和是_______
(2)什么叫正多边形?
制作6个正三角形、正方形、正五边形、正六边形和正七边形,分别动手拼图,观察到底有几种正多边形能够拼成一个平面图形,使它既不留下一丝空白,又不相互重叠。
认真阅读书本P65-P66的内容,并完成P66的表格,回答下面问题:
正多边形能否拼满地板应满足什么样的数学原理呢?
可以拼满地板的正多边形分别需要几个?可以怎样利用数学知识来推导出来?
四、自学测试:P66的练习
导学案9.3 用正多边形拼地板
2.用多种正多边形拼地板
学习目标:
会用多种正多边形进行平面镶嵌
能说明几种正多边形铺满地面的理由
二、学习重点:
通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象等能力
自学指导:
复习:(1)能单独拼满地板的正多边形有哪几种?
(2)用正多边形铺满地板利用的数学原理是什么?
认真阅读书本P66-P67的内容,并回答下面几个问题:
图9.3.3是由哪几种正多边形铺成的?为什么能拼成既没有空隙也没有重叠的平面图形?
图9.3.4呢?
(3)图9.3.6呢?
(4)图9.3.7呢
自学测试:P67的练习2
加强训练:
你能用正三角形、正方形、正十二边形拼成一个不留空隙,不重叠的平面图形吗?
六、课后作业:P67的习题1,2(写出个数即可),3
1.认识三角形 第一课时
学习目标:
了解三角形及三角形的顶点、边、内角、外交等概念
了解三角形按角进行分类
了解等腰三角行、等边三角形(正三角形)
二、学习重点:
1、了解三角形及三角形的顶点、边、内角、外交等概念
2、了解三角形按角进行分类
3、了解等腰三角行、等边三角形(正三角形)
自学指导1:
认真看书本P55,并回答下面问题:
三角形的定义是什么?(用笔画在书上)
如图所示:
①整个三角形可以表示为______________
②三角形有___条边,分别可以表示为_____________________
③三角形有___个顶点,分别可以表示为____________________
④三角形的内角和为_________度
⑤三角形有_____个内角,分别可以表示为________________
⑥什么叫三角形的外角?(用笔画在书上)
⑦一个三角形一共有____个外角
⑧如图所示:请你做出的外角,一共能做出几个?它们有什么样的关系?
自学测试1:
指出图中有几个三角形?并把它们表示出来
指出△ADC的三个内角,三条边,并表示出来
CD是哪两个三角形的公共边?
是△BCD的什么角?是△ACD的什么角?是△ADC的外角吗?
画出相邻的外角
自学指导2:看书本P55-P56的试一试,并回答问题:
三角形按角分类可以分为三种:
_____________ ( )
_____________ ( )
_____________ ( )
三角形按边分类可以分为两种:
_____________
_______________
_____________
_______________
六、自学测试2:
完成书本P56的做一做和练习
导学案9.1 三角形
1.认识三角形 第二课时
学习目标:
1、了解三角形的中线、角平分线、高的概念
2、会画出任意三角形的角平分线、中线和高
3、会利用三角形内角和进行简单的计算
二、学习重点:
三角形中线、角平分线、高的画法
自学指导:
看书本P57的第一段,完成下面几个内容:
什么是三角形的中线?一个三角形有几条中线?完成做一做中的第一个作图。
什么是三角形的角平分线?它和角的平分线有区别吗?一个三角形有几条角平分线?完成做一做中的第二个作图。
什么是三角形的高?锐角三角形、直角三角形和钝角三角形的高画法一样吗?完成做一做中的第三个作图。并画出直角三角形和钝角三角形的三条高
完成P57的做一做中的填空题
自学测试:P57的练习
加强训练:
已知△ABC中,∠A:∠B:∠C=1:2:3,求△ABC各角的度数
已知:AC⊥BC,且∠A=60度,BD是△ABC的一条角平分线,
求:∠ABD的度数。
导学案9.1 三角形内角和与外角和
学习目标:
了解三角形的外角与内角的两条性质
了解三角形的外角和等于360度
会运用三角形内、外角的性质进行简单的计算和初步的说理
二、学习重点:
三角形外角的性质及三角形的外角和
自学指导:
三角形的内角和是多少?
认真阅读书本P57的内容,并完成以下几个问题:
完成P58的做一做
右图所示:
①外角有哪几个?__________________
②内角有哪几个?__________________
③与∠4相邻的内角是_________
④与∠4不相邻的内角是_________
⑤∠1+∠4=________
∠1+______+______=180
从上面两个式子可以发现:_____=_______+_______
即:三角形的外角性质1:___________________________________________
三角形的外角性质2:___________________________________________
完成书本P58的第二个做一做
讨论书本P59的例题1
自学测试:P59-P60的练习1、2、3题
加强训练:
1、如图:∠ACB=______+_______
∠ACD=______+_______
2、∠BED=______+_______
∠DFC=______+_______
∠EDF=______+_______
=______+_______
课后作业:P61的2、3、4
补充练习:
如图:已知:∠AEC=100,∠EOB=70,
且BD平分∠ABC,求:∠OCB度数
已知:∠B=40,∠A=50,∠C=30,求:∠1和∠2
3、已知:∠B=30,∠A=60,∠C=20,
求:∠BDC度数。(提示:辅助线)
4、已知:∠A=∠D+∠C
证明:EA∥FD
导学案9.1 三角形
3.三角形的三边关系
学习目标:
了解构成三角心的条件
知道三角形三边的关系
了解三角形的稳定性
二、学习重点:
三角形三边关系及其简单应用
自学指导:
复习提问:(1)三角形的内角和是多少?三角形的外角和是多少?三角形的外角有什么性质?
(2)如图所示,从A到B,走那一条路最短,
根据的数学原理是什么?
认真阅读书本P60的做一做下面那段话,
并完成做一做,画出三角形。
完成试一试,并讨论什么样的三条线段可以组成一个三角形。
阅读书本P60-P61的后面两段话,理解三角形具有_______性。
在生活中应用的例子有___________和__________,你还可以举出例子吗?
自学测试:P61的练习
加强训练:
下面不可以构成三角形的线段是哪一组( )
A、3,4,6 B、4,6,6 C、4,4,2 D、4,1,3
2、从2,3,6,4中任选三条线段组成一个三角形,
你可以选择哪三条?______________(写出一组即可)
3、木匠在安装木门的时候在门上固定一个木块,这是利用三角形的_____
4、一个三角形的三边分别是2,4,x,则x应满足什么取值范围________,若x为偶数,则x=______
5、已知等腰三角形的其中两条边分别为4和6,则第三条边为______
6、已知等腰三角形的其中两条边分别为2和6,则周长为______
7、已知一个等腰三角形的周长为24cm,其中一条边长为6,则
另外两边长分别为_____________
六、课后作业:P61的1,2,3,4
导学案9.2 多边形的内角和与外角和
第一课时
学习目标:
了解多边形的内角和
了解正多边形的概念
会运用多边形的内角和公式进行简单的计算
二、学习重点:
多边形的内角和公式及其应用
自学指导:
认真阅读书本P62-P63的内容,并回答下面问题:
完成P62中的试一试:说出什么叫四边形,什么叫五边形?
什么叫n边形?又称为什么?
你能区分凸多边形和凹多边形吗?
五边形和六边形分别有多少个内角?多少个外角?n边形呢?
什么叫正多边形?
什么是多边形的对角线?从四边形的一个顶点出发,可以画几条对角线呢?五边形和六边形呢?n边形呢?
将P63的图9.2.3中的三个图形的对角线全部画出来。
完成P63的探索中的表格,并写出n边形的内角和公式。
讨论完成P64的试一试,你能否用这种方法证明出多边形的内角和公式。
自学测试:认真阅读P64的例题,并完成下面题目
1、从六边形的一个顶点出发的对角线有____条,这些对角线将六边形分成_______个三角形
2、十边形的内角和度数是_________
3、一个多边形内角和度数是720度,那么这个多边形是_____边形
4、若一个多边形的每个内角度数都是120度,那么这是一个_____边形.
5、正六边形的每个内角度数都是_____度
五、课后作业:P65的1,2,3
导学案9.2 多边形的内角和与外角和
第二课时
学习目标:
了解多边形的外角和公式
了解从三角形到n边形,从外角到内角的“化归思想”
二、学习重点:
n边形外角和公式及其应用
自学指导:
多边形的内角和公式是________________
三角形的外角和是_________
认真阅读书本P64的第二段话,并完成探索中的表格
自学测试:完成书本P64的练习1,2
加强训练:
五边形的内角和是_____,外角和是______
八边形的外角和比七边形的外角和大,对吗?( )
一个多边形的每个外角都等于60度,这是一个______边形
一个多边形的每个内角都等于120度,这是一个_____边形
一个多边形的每个内角是外角的5倍,则这是一个_____边形
一个多边形的每个内角比外角多120度,则这是一个______边形
一个多边形的内角和是外角和的2倍,则这是一个____边形
补充练习:
1、正六边形的内角和是____,外角和是_____,每个外角等于____度,每个内角等于______度
2、多边形的边每增加一条边,内角和增加___度,外角和增加___度
3、一个多边形的每个外角都等于40度,这是一个______边形
4、一个多边形的每个内角都等于140度,这是一个_____边形
5、一个多边形的每个内角是外角的3倍,则这是一个_____边形
6、一个多边形的每个内角比外角多100度,则这是一个______边形
7、一个多边形的外角和是内角和的,则这是一个____边形
六、课后作业:P70的5,6,7,8,9
导学案9.3 用正多边形拼地板
用相同的正多边形拼地板
学习目标:
知道正三角形、正方形或正六边形可以镶嵌平面
知道拼成一个不留空隙又不重叠的平面图形的关键是n个多边形的内角和相加等于
二、学习重点:
用相同的正多边形“拼地板”
自学指导:
复习:(1)多边形的内角和公式是________,外角和是_______
(2)什么叫正多边形?
制作6个正三角形、正方形、正五边形、正六边形和正七边形,分别动手拼图,观察到底有几种正多边形能够拼成一个平面图形,使它既不留下一丝空白,又不相互重叠。
认真阅读书本P65-P66的内容,并完成P66的表格,回答下面问题:
正多边形能否拼满地板应满足什么样的数学原理呢?
可以拼满地板的正多边形分别需要几个?可以怎样利用数学知识来推导出来?
四、自学测试:P66的练习
导学案9.3 用正多边形拼地板
2.用多种正多边形拼地板
学习目标:
会用多种正多边形进行平面镶嵌
能说明几种正多边形铺满地面的理由
二、学习重点:
通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象等能力
自学指导:
复习:(1)能单独拼满地板的正多边形有哪几种?
(2)用正多边形铺满地板利用的数学原理是什么?
认真阅读书本P66-P67的内容,并回答下面几个问题:
图9.3.3是由哪几种正多边形铺成的?为什么能拼成既没有空隙也没有重叠的平面图形?
图9.3.4呢?
(3)图9.3.6呢?
(4)图9.3.7呢
自学测试:P67的练习2
加强训练:
你能用正三角形、正方形、正十二边形拼成一个不留空隙,不重叠的平面图形吗?
六、课后作业:P67的习题1,2(写出个数即可),3
