数学北师大版(2019)必修第二册 4.2..2两角和与差的正弦、正切公式及其应用 课件(共26张PPT)
文档属性
| 名称 | 数学北师大版(2019)必修第二册 4.2..2两角和与差的正弦、正切公式及其应用 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 952.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
4.2.2 两角和与差的正弦、正切公式及其应用
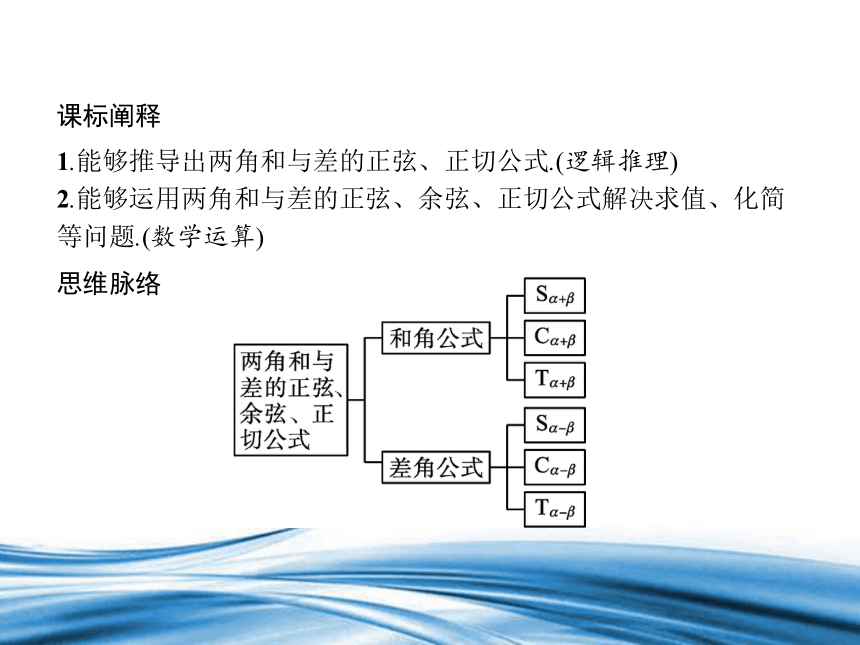
课标阐释
1.能够推导出两角和与差的正弦、正切公式.(逻辑推理)
2.能够运用两角和与差的正弦、余弦、正切公式解决求值、化简等问题.(数学运算)
思维脉络
激趣诱思
知识点拨
在实际生活中,很多的最优化问题都可以转化为三角函数来解决,如停车场的设计、通信电缆的铺设、航海、测量等都有三角函数的影子.求解三角函数问题,都需要三角函数公式转化,今天我们学习两角和与差的正弦、正切公式及其应用,感受三角函数公式的魅力.
激趣诱思
知识点拨
一、两角和与差的正弦公式
名师点析1.两角和的正弦为异名积之和,两角差的正弦为异名积之差,其中角α,β为任意角.
2.上述公式不仅要能够正用,还要善于逆用、变形用.
激趣诱思
知识点拨
微练习
(1)sin 21°cos 39°+cos 21°·sin 39°= .
(2)sin 69°·cos 99°-cos 69°·sin 99°= .
激趣诱思
知识点拨
二、两角和与差的正切公式
激趣诱思
知识点拨
微思考
两角和与差的正切公式中,α,β为任意角吗
激趣诱思
知识点拨
探究一
探究二
探究三
当堂检测
化简与求值
例1化简下列各式:
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
(4)因为(1+tan 21°)(1+tan 24°)=1+tan 21°+tan 24°+tan 21°tan 24°=1+tan(21°+24°)(1-tan 21°tan 24°)+tan 21°tan 24°=1+(1-tan 21°tan 24°)tan 45°+tan 21°tan 24°=1+1-tan 21°tan 24°+tan 21°tan 24°=2.
同理可得(1+tan 22°)(1+tan 23°)=2,
所以原式=2×2=4.
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
利用两角和与差的三角函数公式解决给值求值问题
(1)求sin(α+β)的值;
(2)求cos(α-β)的值;
(3)求tan α的值.
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
反思感悟 给值求值的解题策略
在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角,具体做法是:
(1)当条件中有两角时,一般把“所求角”表示为已知两角的和或差.
(2)当已知角有一个时,可利用诱导公式把所求角转化为已知角.
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
答案(1)0 (2)D
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
反思感悟 根据三角函数值求角时,一般先求出该角的某个三角函数值,再确定该角的取值范围,最后得出该角的大小.至于求该角的哪一个三角函数值,这要取决于该角的取值范围,然后结合三角函数值在不同象限的符号来确定.一般地,若θ∈(0,π),则通常求cos θ;
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
答案A
探究一
探究二
探究三
当堂检测
答案B
探究一
探究二
探究三
当堂检测
解析因为tan 18°+tan 42°+tan 120°
=tan 60°(1-tan 18°tan 42°)+tan 120°
=-tan 60°tan 18°tan 42°,
所以原式=-1.
答案-1
4.2.2 两角和与差的正弦、正切公式及其应用
课标阐释
1.能够推导出两角和与差的正弦、正切公式.(逻辑推理)
2.能够运用两角和与差的正弦、余弦、正切公式解决求值、化简等问题.(数学运算)
思维脉络
激趣诱思
知识点拨
在实际生活中,很多的最优化问题都可以转化为三角函数来解决,如停车场的设计、通信电缆的铺设、航海、测量等都有三角函数的影子.求解三角函数问题,都需要三角函数公式转化,今天我们学习两角和与差的正弦、正切公式及其应用,感受三角函数公式的魅力.
激趣诱思
知识点拨
一、两角和与差的正弦公式
名师点析1.两角和的正弦为异名积之和,两角差的正弦为异名积之差,其中角α,β为任意角.
2.上述公式不仅要能够正用,还要善于逆用、变形用.
激趣诱思
知识点拨
微练习
(1)sin 21°cos 39°+cos 21°·sin 39°= .
(2)sin 69°·cos 99°-cos 69°·sin 99°= .
激趣诱思
知识点拨
二、两角和与差的正切公式
激趣诱思
知识点拨
微思考
两角和与差的正切公式中,α,β为任意角吗
激趣诱思
知识点拨
探究一
探究二
探究三
当堂检测
化简与求值
例1化简下列各式:
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
(4)因为(1+tan 21°)(1+tan 24°)=1+tan 21°+tan 24°+tan 21°tan 24°=1+tan(21°+24°)(1-tan 21°tan 24°)+tan 21°tan 24°=1+(1-tan 21°tan 24°)tan 45°+tan 21°tan 24°=1+1-tan 21°tan 24°+tan 21°tan 24°=2.
同理可得(1+tan 22°)(1+tan 23°)=2,
所以原式=2×2=4.
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
利用两角和与差的三角函数公式解决给值求值问题
(1)求sin(α+β)的值;
(2)求cos(α-β)的值;
(3)求tan α的值.
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
反思感悟 给值求值的解题策略
在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角,具体做法是:
(1)当条件中有两角时,一般把“所求角”表示为已知两角的和或差.
(2)当已知角有一个时,可利用诱导公式把所求角转化为已知角.
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
答案(1)0 (2)D
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
反思感悟 根据三角函数值求角时,一般先求出该角的某个三角函数值,再确定该角的取值范围,最后得出该角的大小.至于求该角的哪一个三角函数值,这要取决于该角的取值范围,然后结合三角函数值在不同象限的符号来确定.一般地,若θ∈(0,π),则通常求cos θ;
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
探究一
探究二
探究三
当堂检测
答案A
探究一
探究二
探究三
当堂检测
答案B
探究一
探究二
探究三
当堂检测
解析因为tan 18°+tan 42°+tan 120°
=tan 60°(1-tan 18°tan 42°)+tan 120°
=-tan 60°tan 18°tan 42°,
所以原式=-1.
答案-1
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
