物理人教版(2019)选择性必修第一册1.3动量守恒定律(共15张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.3动量守恒定律(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-25 11:23:44 | ||
图片预览






文档简介
(共15张PPT)
第十六章 动量守恒定律
第3节 动量守恒定律
水平光滑桌面上做匀速运动的两个小球,质量分别是m1和m2,沿着同一直线向相同的方向运动,速度分别是v1 和v2,v2>v1。当第二个小球追上第一个小球两球碰撞。碰撞后的速度分别是v1′和v2′,仍在原来直线上运动。碰撞过程中第一个小球所受第二个球对它的作用力是F1,第二个小球所受第一个球对它的作用力是F2,碰撞时两球作用时间很短,用 t表示。
一、用牛顿运动定律分析
1、用牛顿第二定律求碰撞过程中两球的加速度
2、F1与F2的关系,注意方向
3、加速度与碰撞前后速度的关系
二、用动量定理分析
1、碰撞过程中对两个小球用动量定理
2、F1与F2的关系,注意方向
最早提出动量概念的是法国科学家笛卡尔,十七世纪,以笛卡儿为代表的西欧的哲学家们提出了这样一种观点:若找到一个适当的物理量来描述,运动的总量是守恒的。这就是运动不灭的思想。他继承伽利略说法,定义质量和速率的乘积为动量。笛卡尔认为,这是量度运动的唯一正确的物理量。他的观点的缺陷,在于忽略了动量的方向性。
1668年,荷兰物理学家惠更斯在《关于碰撞对物体运动的影响》的论文中,明确指出了动量的方向性和守恒性。
牛顿把笛卡尔的定义做了修正,明确的用质量和速度的乘积来定义动量。科学前辈们就是在追寻不变量的努力中,逐渐建立了动量的概念,发现了动量守恒定律。
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
在光滑水平面上,A、B间有一根被压缩的弹簧,当弹簧突然释放后,如图所示,两物块的质量分别为m1和m2。讨论此系统在运动时动量是否守恒?
如果水平地面不光滑,与两物块的动摩擦因素 相同,讨论m1=m2和m1≠m2两种情况下系统的动量是否守恒 ?
一枚在空中飞行的炮弹,炮弹在空中某点突然炸裂成两块
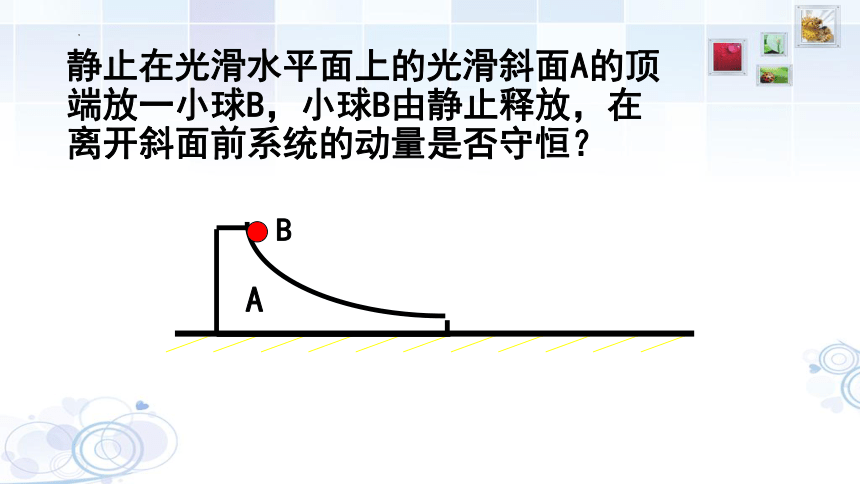
静止在光滑水平面上的光滑斜面A的顶端放一小球B,小球B由静止释放,在离开斜面前系统的动量是否守恒?
A
B
在光滑水平面的车上有一辆平板车,一个人站在车上用大锤敲打车的左端.在连续的敲打下,这辆车能持续地向右运动吗 说明理由.
四性:
①矢量性:
解题时要规定正方向
②.系统性:
应用于系统
③.相对性:
速度必须对同一参考系
④.同时性:
速度分别是作用前后同一
时刻的速度
1.把一支枪水平固定在小车上,小车放在光滑的水平地面上,枪发射出一颗子弹时,关于枪、弹、车,下列说法正确的是( )
A.枪和子弹组成的系统,动量守恒
B.枪和车组成的系统动量守恒
C.枪、弹、车三者组成的系统动量守恒
D.枪、弹、车三者组成的系统,因枪和子弹间有摩擦力,故动量不守恒
C
2:在列车编组站里,一辆m1=1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
解:沿碰撞前货车运动的方向建立坐标轴,设两车结合后的速度为v。
两车碰撞前的总动量为
碰撞后的总动量为
由动量守恒定律p′=p可得
所以
两车结合后速度大小是0.9m/s,是正值,表示结合后仍然沿坐标轴的方向运动,即仍然向右运动。
3、爆炸
一枚在空中飞行的炮弹,质量m=300kg,在某点的速度为v=60m/s,方向水平。炮弹在该点突然炸裂成两块,其中质量为m1=200kg的一块沿着与v相同方向飞去,速度为v1=120m/s。求炸裂后另一块m2的速度v2。
动量守恒定律解题的一般步骤:
(1)分析题意,明确研究对象;
(2)受力分析,明确系统的内力和外力,判断是否满足守恒条件;
(3)选定正方向根据动量守恒定律列出方程;
(4)统一单位,求解,得出结论。
小结:
4、动量守恒定律适用的范围:
1、动量守恒定律:
2、公式表达:
⑴系统不受外力或所受外力的矢量和为0;
3、适用条件:
⑵系统内力远大于外力。(3)某个方向上动量守恒
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
动量守恒定律是自然界普遍适用的基本规律,对宏观低速运动的物体系统,或微观高速的系统它都是适用的。
第十六章 动量守恒定律
第3节 动量守恒定律
水平光滑桌面上做匀速运动的两个小球,质量分别是m1和m2,沿着同一直线向相同的方向运动,速度分别是v1 和v2,v2>v1。当第二个小球追上第一个小球两球碰撞。碰撞后的速度分别是v1′和v2′,仍在原来直线上运动。碰撞过程中第一个小球所受第二个球对它的作用力是F1,第二个小球所受第一个球对它的作用力是F2,碰撞时两球作用时间很短,用 t表示。
一、用牛顿运动定律分析
1、用牛顿第二定律求碰撞过程中两球的加速度
2、F1与F2的关系,注意方向
3、加速度与碰撞前后速度的关系
二、用动量定理分析
1、碰撞过程中对两个小球用动量定理
2、F1与F2的关系,注意方向
最早提出动量概念的是法国科学家笛卡尔,十七世纪,以笛卡儿为代表的西欧的哲学家们提出了这样一种观点:若找到一个适当的物理量来描述,运动的总量是守恒的。这就是运动不灭的思想。他继承伽利略说法,定义质量和速率的乘积为动量。笛卡尔认为,这是量度运动的唯一正确的物理量。他的观点的缺陷,在于忽略了动量的方向性。
1668年,荷兰物理学家惠更斯在《关于碰撞对物体运动的影响》的论文中,明确指出了动量的方向性和守恒性。
牛顿把笛卡尔的定义做了修正,明确的用质量和速度的乘积来定义动量。科学前辈们就是在追寻不变量的努力中,逐渐建立了动量的概念,发现了动量守恒定律。
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
在光滑水平面上,A、B间有一根被压缩的弹簧,当弹簧突然释放后,如图所示,两物块的质量分别为m1和m2。讨论此系统在运动时动量是否守恒?
如果水平地面不光滑,与两物块的动摩擦因素 相同,讨论m1=m2和m1≠m2两种情况下系统的动量是否守恒 ?
一枚在空中飞行的炮弹,炮弹在空中某点突然炸裂成两块
静止在光滑水平面上的光滑斜面A的顶端放一小球B,小球B由静止释放,在离开斜面前系统的动量是否守恒?
A
B
在光滑水平面的车上有一辆平板车,一个人站在车上用大锤敲打车的左端.在连续的敲打下,这辆车能持续地向右运动吗 说明理由.
四性:
①矢量性:
解题时要规定正方向
②.系统性:
应用于系统
③.相对性:
速度必须对同一参考系
④.同时性:
速度分别是作用前后同一
时刻的速度
1.把一支枪水平固定在小车上,小车放在光滑的水平地面上,枪发射出一颗子弹时,关于枪、弹、车,下列说法正确的是( )
A.枪和子弹组成的系统,动量守恒
B.枪和车组成的系统动量守恒
C.枪、弹、车三者组成的系统动量守恒
D.枪、弹、车三者组成的系统,因枪和子弹间有摩擦力,故动量不守恒
C
2:在列车编组站里,一辆m1=1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
解:沿碰撞前货车运动的方向建立坐标轴,设两车结合后的速度为v。
两车碰撞前的总动量为
碰撞后的总动量为
由动量守恒定律p′=p可得
所以
两车结合后速度大小是0.9m/s,是正值,表示结合后仍然沿坐标轴的方向运动,即仍然向右运动。
3、爆炸
一枚在空中飞行的炮弹,质量m=300kg,在某点的速度为v=60m/s,方向水平。炮弹在该点突然炸裂成两块,其中质量为m1=200kg的一块沿着与v相同方向飞去,速度为v1=120m/s。求炸裂后另一块m2的速度v2。
动量守恒定律解题的一般步骤:
(1)分析题意,明确研究对象;
(2)受力分析,明确系统的内力和外力,判断是否满足守恒条件;
(3)选定正方向根据动量守恒定律列出方程;
(4)统一单位,求解,得出结论。
小结:
4、动量守恒定律适用的范围:
1、动量守恒定律:
2、公式表达:
⑴系统不受外力或所受外力的矢量和为0;
3、适用条件:
⑵系统内力远大于外力。(3)某个方向上动量守恒
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
动量守恒定律是自然界普遍适用的基本规律,对宏观低速运动的物体系统,或微观高速的系统它都是适用的。
