青岛版七年级数学下册 8.4 对顶角课件(共15张PPT)
文档属性
| 名称 | 青岛版七年级数学下册 8.4 对顶角课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 10:14:01 | ||
图片预览




文档简介
(共16张PPT)
8.4 对顶角
旧知回顾
2、什么样的两个角互为补角?
4、若∠1与∠2互补,则∠1+∠2=_________°;
5、30°的余角是______°,补角是______°若一个角的度数是x(x<90 °) ,则它的余角的度数和补角的度数是 ;
6、60°角的余角的补角是_______°.
1、什么是平角?平角等于多少度?“平角就是直线”对吗?
3、补角有什么性质?
1.掌握对顶角的定义并能够在图形中识别出来.
2.能够用对顶角的性质解决有关的问题.
学习目标
如图,把两根木条用钉子钉在一起,转动其中一根木条,
观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗
课堂探究
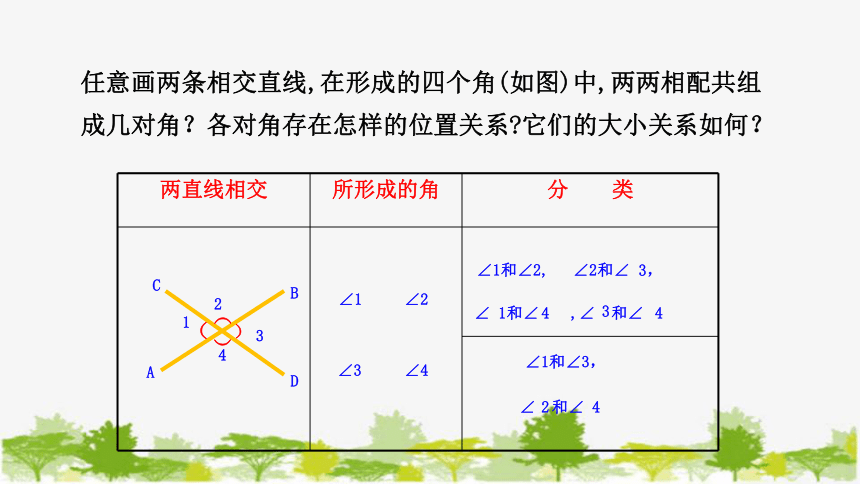
任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系 它们的大小关系如何?
两直线相交 所形成的角 分 类
A
B
C
D
)
(
1
3
4
2
)
(
∠3
∠1
∠2
∠4
∠1和∠2,
4
∠2和∠
∠ 和∠
,∠ 和∠
1
4
3
4
∠1和∠3,
∠ 和∠
2
3,
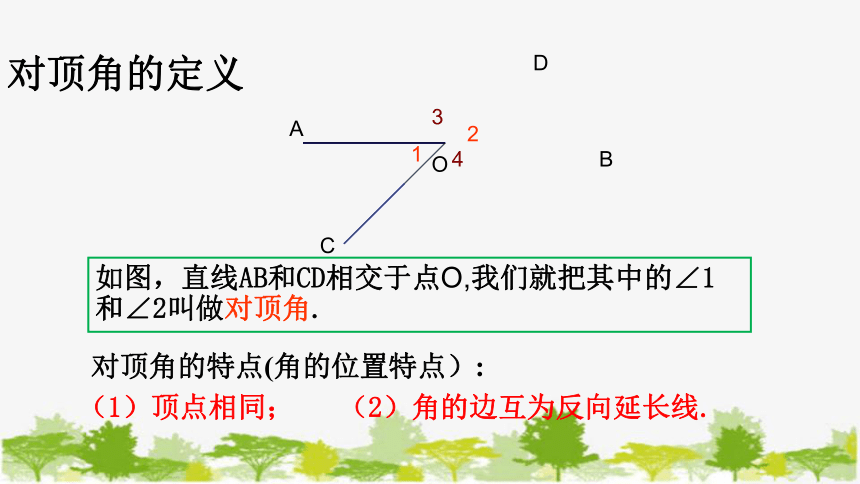
如图,直线AB和CD相交于点O,我们就把其中的∠1和∠2叫做对顶角.
3
4
D
B
C
O
A
2
1
对顶角的定义
对顶角的特点(角的位置特点):
(1)顶点相同;
(2)角的边互为反向延长线.
练一练
1、下列各选项中,∠1和∠2是对顶角的是( )
C
(1)
(2)
(3)
2
6
12
(4)
20
……
……
……
若有n条直线相交于一点O,那么有 对对顶角.
2、下图中有几对对顶角?
(n-1)n
1
2
3
4
m
n
对顶角相等
这个推理过程可以写成:
因为∠1+∠2=180 ° , ∠3+∠2=180 °
(平角定义)
(同角的补角相等)
所以∠ 1= ∠3
如图,∠1、∠3有怎样的大小关系?
(
对顶角的性质
(
(
(
课本17页例1:
如图,直线AB和CD相交于点O, 射线OE是∠BOD的角平分线,已知∠AOD=110°, 求∠COB,∠AOC,∠BOE,∠EOD的度数.
A
B
C
O
D
E
解:因为∠COB与∠AOD是对顶角,
所以∠COB= ∠AOD=110°
∠AOC = ∠COD - ∠AOD
=180° -110°= 70°
由OE平分∠BOD,得
∠BOE=∠EOD= ∠BOD=0.5×70°=35°
1、对顶角定义
2、对顶角相等
小结
2、已知:直线a,b相交∠1=40°.
求∠2,∠3,∠4的度数?
a
b
1
2
3
4
解:∠3=∠1=40° (对顶角相等),
∠2=180°-∠1=180°-40°=140°(平角的定义),
∠4=∠2=140°(对顶角相等).
1、已知∠α 和∠β 是对顶角,若∠α=30°,则∠β 的度
数为( )
A.30° B.60° C.70° D.150°
A
巩固练习
A
3、如图,已知直线AB 和CD 相交于点O,OA 平分∠EOC,若∠BOD =35°,求∠EOC 的度数.
解:因为OA 平分∠EOC,
所以∠EOC=2∠AOC.
又因为∠AOC=∠BOD ,∠BOD =35°,
所以∠EOC=2∠BOD =70°.
4、为了实地测量某古塔外墙底部墙角,如图,你能在不进入塔内的情况下设计出测量∠ABC 大小的方案吗 你能设计几种方案
分析:将要求的角转化为图形外的角.
方案一:延长AB 至点D→ 测量∠CBD→ 平角的概念→ 求∠ABC.
方案二:构造对顶角→ 测量对顶角的度数.
解:能.
方案一:如图8.4G8①,延长AB 至点D .量出∠CBD 的度数,
则∠ABC=180°-∠CBD (互补的概念).
方案二:如图8.4G8②,延长CB 至点E,延长AB 至点F.量出∠EBF 的度数,则∠ABC=∠EBF(对顶角相等).
8.4 对顶角
旧知回顾
2、什么样的两个角互为补角?
4、若∠1与∠2互补,则∠1+∠2=_________°;
5、30°的余角是______°,补角是______°若一个角的度数是x(x<90 °) ,则它的余角的度数和补角的度数是 ;
6、60°角的余角的补角是_______°.
1、什么是平角?平角等于多少度?“平角就是直线”对吗?
3、补角有什么性质?
1.掌握对顶角的定义并能够在图形中识别出来.
2.能够用对顶角的性质解决有关的问题.
学习目标
如图,把两根木条用钉子钉在一起,转动其中一根木条,
观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗
课堂探究
任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系 它们的大小关系如何?
两直线相交 所形成的角 分 类
A
B
C
D
)
(
1
3
4
2
)
(
∠3
∠1
∠2
∠4
∠1和∠2,
4
∠2和∠
∠ 和∠
,∠ 和∠
1
4
3
4
∠1和∠3,
∠ 和∠
2
3,
如图,直线AB和CD相交于点O,我们就把其中的∠1和∠2叫做对顶角.
3
4
D
B
C
O
A
2
1
对顶角的定义
对顶角的特点(角的位置特点):
(1)顶点相同;
(2)角的边互为反向延长线.
练一练
1、下列各选项中,∠1和∠2是对顶角的是( )
C
(1)
(2)
(3)
2
6
12
(4)
20
……
……
……
若有n条直线相交于一点O,那么有 对对顶角.
2、下图中有几对对顶角?
(n-1)n
1
2
3
4
m
n
对顶角相等
这个推理过程可以写成:
因为∠1+∠2=180 ° , ∠3+∠2=180 °
(平角定义)
(同角的补角相等)
所以∠ 1= ∠3
如图,∠1、∠3有怎样的大小关系?
(
对顶角的性质
(
(
(
课本17页例1:
如图,直线AB和CD相交于点O, 射线OE是∠BOD的角平分线,已知∠AOD=110°, 求∠COB,∠AOC,∠BOE,∠EOD的度数.
A
B
C
O
D
E
解:因为∠COB与∠AOD是对顶角,
所以∠COB= ∠AOD=110°
∠AOC = ∠COD - ∠AOD
=180° -110°= 70°
由OE平分∠BOD,得
∠BOE=∠EOD= ∠BOD=0.5×70°=35°
1、对顶角定义
2、对顶角相等
小结
2、已知:直线a,b相交∠1=40°.
求∠2,∠3,∠4的度数?
a
b
1
2
3
4
解:∠3=∠1=40° (对顶角相等),
∠2=180°-∠1=180°-40°=140°(平角的定义),
∠4=∠2=140°(对顶角相等).
1、已知∠α 和∠β 是对顶角,若∠α=30°,则∠β 的度
数为( )
A.30° B.60° C.70° D.150°
A
巩固练习
A
3、如图,已知直线AB 和CD 相交于点O,OA 平分∠EOC,若∠BOD =35°,求∠EOC 的度数.
解:因为OA 平分∠EOC,
所以∠EOC=2∠AOC.
又因为∠AOC=∠BOD ,∠BOD =35°,
所以∠EOC=2∠BOD =70°.
4、为了实地测量某古塔外墙底部墙角,如图,你能在不进入塔内的情况下设计出测量∠ABC 大小的方案吗 你能设计几种方案
分析:将要求的角转化为图形外的角.
方案一:延长AB 至点D→ 测量∠CBD→ 平角的概念→ 求∠ABC.
方案二:构造对顶角→ 测量对顶角的度数.
解:能.
方案一:如图8.4G8①,延长AB 至点D .量出∠CBD 的度数,
则∠ABC=180°-∠CBD (互补的概念).
方案二:如图8.4G8②,延长CB 至点E,延长AB 至点F.量出∠EBF 的度数,则∠ABC=∠EBF(对顶角相等).
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
