沪科版数学九年级下册第24章 圆 单元测试卷(word版 含解析)
文档属性
| 名称 | 沪科版数学九年级下册第24章 圆 单元测试卷(word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 00:00:00 | ||
图片预览


文档简介
《第24章 圆》
一、选择题(共8小题,每小题3分,满分24分)
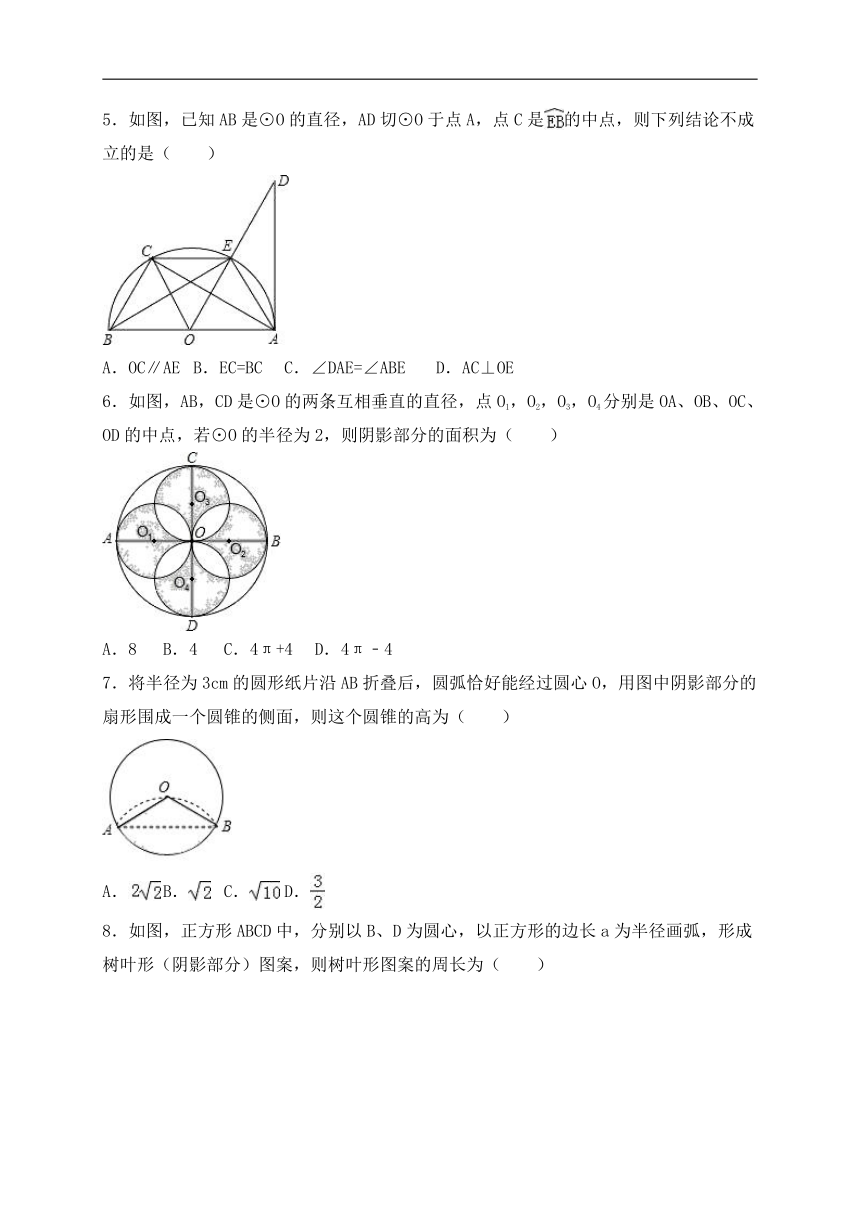
1.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
2.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )
A.4 B.8 C.2 D.4
3.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.90° B.60° C.45° D.30°
4.如图,已知⊙O1的半径为1cm,⊙O2的半径为2cm,将⊙O1,⊙O2放置在直线l上,如果⊙O1在直线l上任意滚动,那么圆心距O1O2的长不可能是( )
A.6cm B.3cm C.2cm D.0.5cm
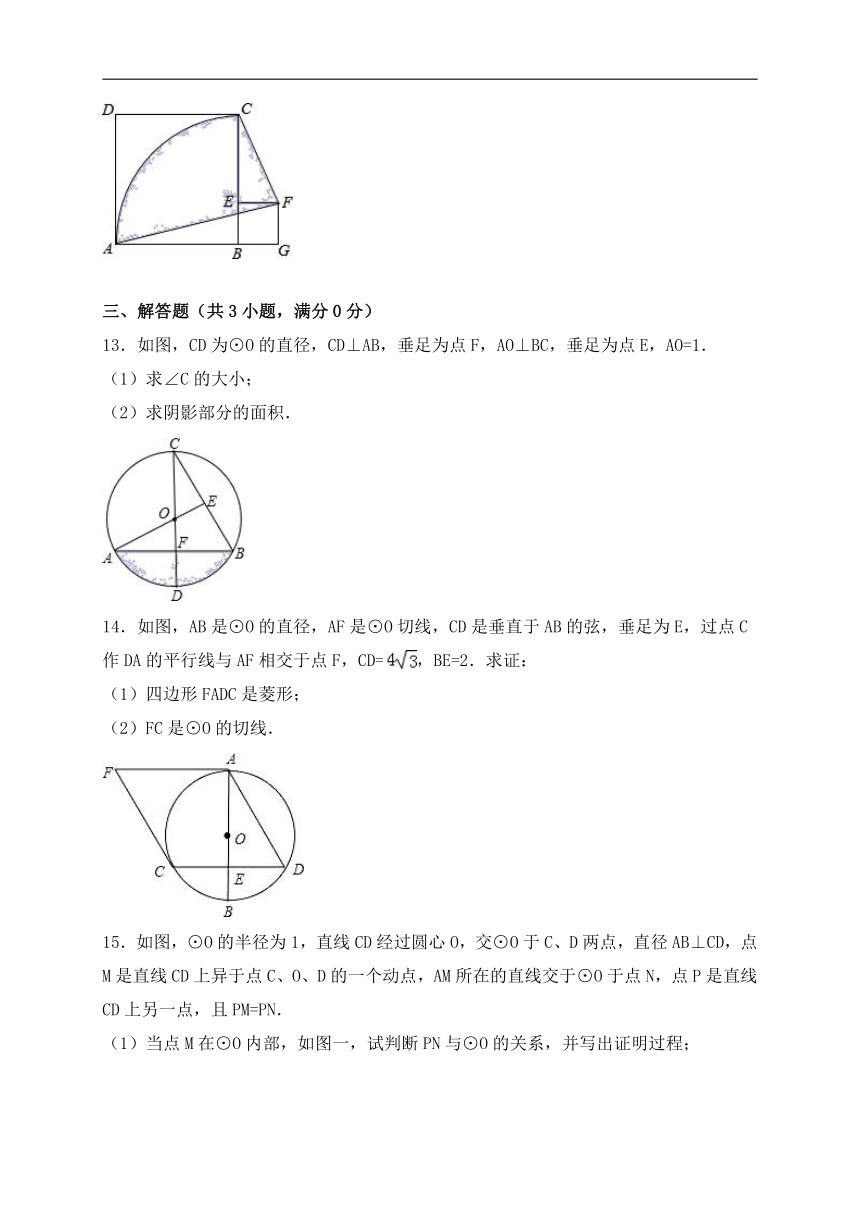
5.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
6.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
7.将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
A. B. C. D.
8.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B.2πa C. D.3a
二、填空题(共4小题,每小题3分,满分12分)
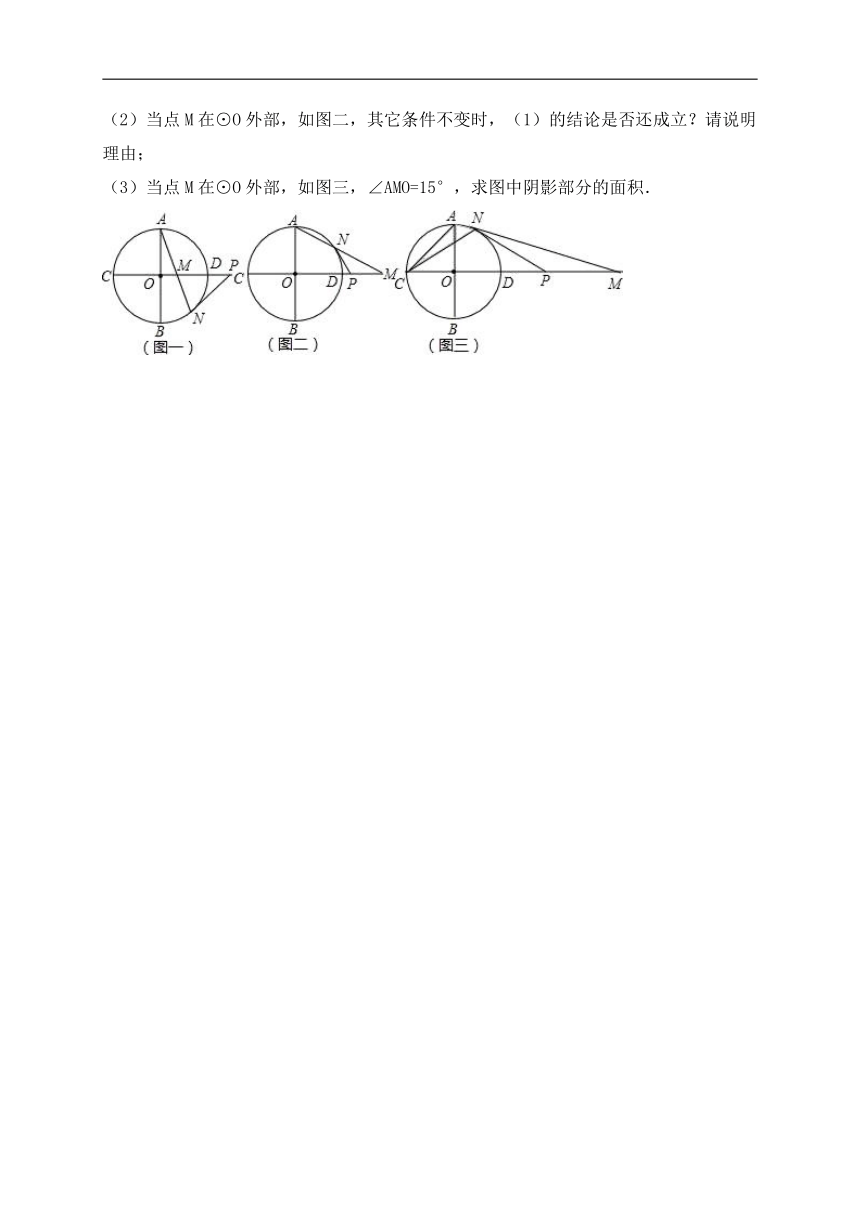
9.如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 度.
10.如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
11.已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 cm.
12.如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为 .
三、解答题(共3小题,满分0分)
13.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小;
(2)求阴影部分的面积.
14.如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=,BE=2.求证:
(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
15.如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
《第24章 圆》
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
【考点】圆周角定理.
【分析】过A、O作⊙O的直径AD,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质求出θ=2α+2β.
【解答】解:过A作⊙O的直径,交⊙O于D;
在△OAB中,OA=OB,
则∠BOD=∠OBA+∠OAB=2×32°=64°,
同理可得:∠COD=∠OCA+∠OAC=2×38°=76°,
故∠BOC=∠BOD+∠COD=140°.
故选D
【点评】本题考查了圆周角定理,涉及了等腰三角形的性质及三角形的外角性质,解答本题的关键是求出∠COD及∠BOD的度数.
2.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )
A.4 B.8 C.2 D.4
【考点】垂径定理;勾股定理.
【专题】探究型.
【分析】先根据⊙O的直径AB=12求出OB的长,再由BP:AP=1:5求出BP的长,故可得出OP的长,连接OC,在Rt△OPC中利用勾股定理可求出PC的长,再根据垂径定理即可得出结论.
【解答】解:∵⊙O的直径AB=12,
∴OB=AB=6,
∵BP:AP=1:5,
∴BP=AB=×12=2,
∴OP=OB﹣BP=6﹣2=4,
∵CD⊥AB,
∴CD=2PC.
如图,连接OC,在Rt△OPC中,
∵OC=6,OP=4,
∴PC===2,
∴CD=2PC=2×2=4.
故选D.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
3.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.90° B.60° C.45° D.30°
【考点】切线的性质;含30度角的直角三角形.
【分析】当AP与⊙O相切时,∠OAP有最大值,连结OP,根据切线的性质得OP⊥AP,由OB=AB得OA=2OP,然后根据含30度的直角三角形三边的关系即可得到此时∠OAP的度数.
【解答】解:当AP与⊙O相切时,∠OAP有最大值,连结OP,如图,
则OP⊥AP,
∵OB=AB,
∴OA=2OP,
∴∠PAO=30°.
故选D.
【点评】本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了含30度的直角三角形三边的关系.
4.如图,已知⊙O1的半径为1cm,⊙O2的半径为2cm,将⊙O1,⊙O2放置在直线l上,如果⊙O1在直线l上任意滚动,那么圆心距O1O2的长不可能是( )
A.6cm B.3cm C.2cm D.0.5cm
【考点】圆与圆的位置关系.
【分析】根据在滚动的过程中两圆的位置关系可以确定圆心距的关系.
【解答】解:∵⊙O1的半径为1cm,⊙O2的半径为2cm,
∴当两圆内切时,圆心距为1,
∵⊙O1在直线l上任意滚动,
∴两圆不可能内含,
∴圆心距不能小于1,
故选D.
【点评】本题考查了两圆的位置关系,本题中两圆不可能内含.
5.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
【考点】切线的性质;圆心角、弧、弦的关系;圆周角定理.
【专题】计算题.
【分析】由C为弧EB的中点,利用垂径定理的逆定理得出OC垂直于BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE垂直于BE,即可确定出OC与AE平行,选项A正确;
由C为弧BE中点,即弧BC=弧CE,利用等弧对等弦,得到BC=EC,选项B正确;
由AD为圆的切线,得到AD垂直于OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等得到∠DAE=∠ABE,选项C正确;
AC不一定垂直于OE,选项D错误.
【解答】解:A、∵点C是的中点,
∴OC⊥BE,
∵AB为圆O的直径,
∴AE⊥BE,
∴OC∥AE,本选项正确;
B、∵=,
∴BC=CE,本选项正确;
C、∵AD为圆O的切线,
∴AD⊥OA,
∴∠DAE+∠EAB=90°,
∵∠EBA+∠EAB=90°,
∴∠DAE=∠EBA,本选项正确;
D、AC不一定垂直于OE,本选项错误,
故选D
【点评】此题考查了切线的性质,圆周角定理,以及圆心角,弧及弦之间的关系,熟练掌握切线的性质是解本题的关键.
6.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
【考点】扇形面积的计算;圆与圆的位置关系.
【分析】首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.
【解答】解:如图所示:
可得正方形EFMN,边长为2,
正方形中两部分阴影面积为:22﹣π×12=4﹣π,
∴正方形内空白面积为:4﹣2(4﹣π)=2π﹣4,
∵⊙O的半径为2,
∴O1,O2,O3,O4的半径为1,
∴小圆的面积为:π×12=π,
扇形COB的面积为: =π,
∴扇形COB中两空白面积相等,
∴阴影部分的面积为:π×22﹣2(2π﹣4)=8.
故选A.
【点评】此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.
7.将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
A. B. C. D.
【考点】圆锥的计算.
【分析】过O点作OC⊥AB,垂足为D,交⊙O于点C,由折叠的性质可知OD为半径的一半,而OA为半径,可求∠A=30°,同理可得∠B=30°,在△AOB中,由内角和定理求∠AOB,然后求得弧AB的长,利用弧长公式求得围成的圆锥的底面半径,最后利用勾股定理求得其高即可.
【解答】解:过O点作OC⊥AB,垂足为D,交⊙O于点C,
由折叠的性质可知,OD=OC=OA,
由此可得,在Rt△AOD中,∠A=30°,
同理可得∠B=30°,
在△AOB中,由内角和定理,
得∠AOB=180°﹣∠A﹣∠B=120°
∴弧AB的长为=2π
设围成的圆锥的底面半径为r,
则2πr=2π
∴r=1cm
∴圆锥的高为=2
故选A.
【点评】本题考查了垂径定理,折叠的性质,特殊直角三角形的判断.关键是由折叠的性质得出含30°的直角三角形.
8.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B.2πa C. D.3a
【考点】弧长的计算.
【分析】由图可知,阴影部分的周长是两个圆心角为90°、半径为a的扇形的弧长,可据此求出阴影部分的周长.
【解答】解:∵四边形ABCD是边长为a正方形,
∴∠B=∠D=90°,AB=CB=AD=CD=a,
∴树叶形图案的周长=×2=πa.
故选A.
【点评】本题考查了弧长的计算.解答该题时,需要牢记弧长公式l=(R是半径).
二、填空题(共4小题,每小题3分,满分12分)
9.如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 48 度.
【考点】垂径定理.
【专题】几何图形问题.
【分析】根据点D是弦AC的中点,得到OD⊥AC,然后根据∠DOC=∠DOA即可求得答案.
【解答】解:∵AB是⊙O的直径,
∴OA=OC
∵∠A=42°
∴∠ACO=∠A=42°
∵D为AC的中点,
∴OD⊥AC,
∴∠DOC=90°﹣∠DCO=90°﹣42°=48°.
故答案为:48.
【点评】本题考查了垂径定理的知识,解题的关键是根的弦的中点得到弦的垂线.
10.如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
【考点】旋转的性质;弧长的计算.
【分析】根据Rt△ABC中的30°角所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半以及旋转的性质推知△AA′C是等边三角形,所以根据等边三角形的性质利用弧长公式来求CA′旋转所构成的扇形的弧长.
【解答】解:∵在Rt△ABC中,∠B=30°,AB=10cm,
∴AC=AB=5cm.
根据旋转的性质知,A′C=AC,
∴A′C=AB=5cm,
∴点A′是斜边AB的中点,
∴AA′=AB=5cm,
∴AA′=A′C=AC,
∴∠A′CA=60°,
∴CA′旋转所构成的扇形的弧长为: =(cm).
故答案是:.
【点评】本题考查了弧长的计算、旋转的性质.解题的难点是推知点A′是斜边AB的中点,同时,这也是解题的关键.
11.已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 25 cm.
【考点】圆锥的计算.
【分析】首先利用扇形的弧长公式求得扇形的弧长,然后利用圆的周长公式即可求解.
【解答】解:扇形的弧长是: =50πcm,
设底面半径是rcm,则2πr=50π,
解得:r=25.
故答案是:25.
【点评】考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
12.如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为 4π .
【考点】正方形的性质;整式的混合运算.
【专题】压轴题.
【分析】设正方形EFGB的边长为a,表示出CE、AG,然后根据阴影部分的面积=S扇形ABC+S正方形EFGB+S△CEF﹣S△AGF,列式计算即可得解.
【解答】解:设正方形EFGB的边长为a,则CE=4﹣a,AG=4+a,
阴影部分的面积=S扇形ABC+S正方形EFGB+S△CEF﹣S△AGF
=+a2+a(4﹣a)﹣a(4+a)
=4π+a2+2a﹣a2﹣2a﹣a2
=4π.
故答案为:4π.
【点评】本题考查了正方形的性质,整式的混合运算,扇形的面积计算,引入小正方形的边长这一中间量是解题的关键.
三、解答题(共3小题,满分0分)
13.(2013 威海)如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小;
(2)求阴影部分的面积.
【考点】垂径定理;圆心角、弧、弦的关系;扇形面积的计算.
【分析】(1)根据垂径定理可得=,∠C=∠AOD,然后在Rt△COE中可求出∠C的度数.
(2)连接OB,根据(1)可求出∠AOB=120°,在Rt△AOF中,求出AF,OF,然后根据S阴影=S扇形OAB﹣S△OAB,即可得出答案.
【解答】解:(1)∵CD是圆O的直径,CD⊥AB,
∴=,
∴∠C=∠AOD,
∵∠AOD=∠COE,
∴∠C=∠COE,
∵AO⊥BC,
∴∠C=30°.
(2)连接OB,
由(1)知,∠C=30°,
∴∠AOD=60°,
∴∠AOB=120°,
在Rt△AOF中,AO=1,∠AOF=60°,
∴AF=,OF=,
∴AB=,
∴S阴影=S扇形OADB﹣S△OAB=﹣××=π﹣.
【点评】本题考查了垂径定理及扇形的面积计算,解答本题的关键是利用解直角三角形的知识求出∠C、∠AOB的度数,难度一般.
14.(2013 聊城)如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=,BE=2.求证:
(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
【考点】切线的判定与性质;菱形的判定.
【专题】压轴题.
【分析】(1)首先连接OC,由垂径定理,可求得CE的长,又由勾股定理,可求得半径OC的长,然后由勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平行四边形,继而证得四边形FADC是菱形;
(2)首先连接OF,易证得△AFO≌△CFO,继而可证得FC是⊙O的切线.
【解答】证明:(1)连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=CD=×4=2,
设OC=x,
∵BE=2,
∴OE=x﹣2,
在Rt△OCE中,OC2=OE2+CE2,
∴x2=(x﹣2)2+(2)2,
解得:x=4,
∴OA=OC=4,OE=2,
∴AE=6,
在Rt△AED中,AD==4,
∴AD=CD,
∵AF是⊙O切线,
∴AF⊥AB,
∵CD⊥AB,
∴AF∥CD,
∵CF∥AD,
∴四边形FADC是平行四边形,
∵AD=CD,
∴平行四边形FADC是菱形;
(2)连接OF,AC,
∵四边形FADC是菱形,
∴FA=FC,
∴∠FAC=∠FCA,
∵AO=CO,
∴∠OAC=∠OCA,
∴∠FAC+∠OAC=∠FCA+∠OCA,
即∠OCF=∠OAF=90°,
即OC⊥FC,
∵点C在⊙O上,
∴FC是⊙O的切线.
【点评】此题考查了切线的判定与性质、菱形的判定与性质、垂径定理、勾股定理以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
15.(2013 莱芜)如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
【考点】圆的综合题.
【专题】压轴题.
【分析】(1)根据切线的判定得出∠PNO=∠PNM+∠ONA=∠AMO+∠ONA进而求出即可;
(2)根据已知得出∠PNM+∠ONA=90°,进而得出∠PNO=180°﹣90°=90°即可得出答案;
(3)首先根据外角的性质得出∠AON=30°进而利用扇形面积公式得出即可.
【解答】(1)PN与⊙O相切.
证明:连接ON,
则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°.
即PN与⊙O相切.
(2)成立.
证明:连接ON,
则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,
∵∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°.
∴∠PNO=180°﹣90°=90°.
即PN与⊙O相切.
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,
∴∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,
则NE=ON sin60°=1×=.
S阴影=S△AOC+S扇形AON﹣S△CON
=OC OA+CO NE
=×1×1+π﹣×1×
=+π﹣.
【点评】此题主要考查了扇形面积公式以及切线的判定等知识,熟练根据切线的判定得出对应角的度数是解题关键.
一、选择题(共8小题,每小题3分,满分24分)
1.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
2.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )
A.4 B.8 C.2 D.4
3.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.90° B.60° C.45° D.30°
4.如图,已知⊙O1的半径为1cm,⊙O2的半径为2cm,将⊙O1,⊙O2放置在直线l上,如果⊙O1在直线l上任意滚动,那么圆心距O1O2的长不可能是( )
A.6cm B.3cm C.2cm D.0.5cm
5.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
6.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
7.将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
A. B. C. D.
8.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B.2πa C. D.3a
二、填空题(共4小题,每小题3分,满分12分)
9.如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 度.
10.如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
11.已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 cm.
12.如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为 .
三、解答题(共3小题,满分0分)
13.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小;
(2)求阴影部分的面积.
14.如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=,BE=2.求证:
(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
15.如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
《第24章 圆》
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
【考点】圆周角定理.
【分析】过A、O作⊙O的直径AD,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质求出θ=2α+2β.
【解答】解:过A作⊙O的直径,交⊙O于D;
在△OAB中,OA=OB,
则∠BOD=∠OBA+∠OAB=2×32°=64°,
同理可得:∠COD=∠OCA+∠OAC=2×38°=76°,
故∠BOC=∠BOD+∠COD=140°.
故选D
【点评】本题考查了圆周角定理,涉及了等腰三角形的性质及三角形的外角性质,解答本题的关键是求出∠COD及∠BOD的度数.
2.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )
A.4 B.8 C.2 D.4
【考点】垂径定理;勾股定理.
【专题】探究型.
【分析】先根据⊙O的直径AB=12求出OB的长,再由BP:AP=1:5求出BP的长,故可得出OP的长,连接OC,在Rt△OPC中利用勾股定理可求出PC的长,再根据垂径定理即可得出结论.
【解答】解:∵⊙O的直径AB=12,
∴OB=AB=6,
∵BP:AP=1:5,
∴BP=AB=×12=2,
∴OP=OB﹣BP=6﹣2=4,
∵CD⊥AB,
∴CD=2PC.
如图,连接OC,在Rt△OPC中,
∵OC=6,OP=4,
∴PC===2,
∴CD=2PC=2×2=4.
故选D.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
3.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.90° B.60° C.45° D.30°
【考点】切线的性质;含30度角的直角三角形.
【分析】当AP与⊙O相切时,∠OAP有最大值,连结OP,根据切线的性质得OP⊥AP,由OB=AB得OA=2OP,然后根据含30度的直角三角形三边的关系即可得到此时∠OAP的度数.
【解答】解:当AP与⊙O相切时,∠OAP有最大值,连结OP,如图,
则OP⊥AP,
∵OB=AB,
∴OA=2OP,
∴∠PAO=30°.
故选D.
【点评】本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了含30度的直角三角形三边的关系.
4.如图,已知⊙O1的半径为1cm,⊙O2的半径为2cm,将⊙O1,⊙O2放置在直线l上,如果⊙O1在直线l上任意滚动,那么圆心距O1O2的长不可能是( )
A.6cm B.3cm C.2cm D.0.5cm
【考点】圆与圆的位置关系.
【分析】根据在滚动的过程中两圆的位置关系可以确定圆心距的关系.
【解答】解:∵⊙O1的半径为1cm,⊙O2的半径为2cm,
∴当两圆内切时,圆心距为1,
∵⊙O1在直线l上任意滚动,
∴两圆不可能内含,
∴圆心距不能小于1,
故选D.
【点评】本题考查了两圆的位置关系,本题中两圆不可能内含.
5.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
【考点】切线的性质;圆心角、弧、弦的关系;圆周角定理.
【专题】计算题.
【分析】由C为弧EB的中点,利用垂径定理的逆定理得出OC垂直于BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE垂直于BE,即可确定出OC与AE平行,选项A正确;
由C为弧BE中点,即弧BC=弧CE,利用等弧对等弦,得到BC=EC,选项B正确;
由AD为圆的切线,得到AD垂直于OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等得到∠DAE=∠ABE,选项C正确;
AC不一定垂直于OE,选项D错误.
【解答】解:A、∵点C是的中点,
∴OC⊥BE,
∵AB为圆O的直径,
∴AE⊥BE,
∴OC∥AE,本选项正确;
B、∵=,
∴BC=CE,本选项正确;
C、∵AD为圆O的切线,
∴AD⊥OA,
∴∠DAE+∠EAB=90°,
∵∠EBA+∠EAB=90°,
∴∠DAE=∠EBA,本选项正确;
D、AC不一定垂直于OE,本选项错误,
故选D
【点评】此题考查了切线的性质,圆周角定理,以及圆心角,弧及弦之间的关系,熟练掌握切线的性质是解本题的关键.
6.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
【考点】扇形面积的计算;圆与圆的位置关系.
【分析】首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.
【解答】解:如图所示:
可得正方形EFMN,边长为2,
正方形中两部分阴影面积为:22﹣π×12=4﹣π,
∴正方形内空白面积为:4﹣2(4﹣π)=2π﹣4,
∵⊙O的半径为2,
∴O1,O2,O3,O4的半径为1,
∴小圆的面积为:π×12=π,
扇形COB的面积为: =π,
∴扇形COB中两空白面积相等,
∴阴影部分的面积为:π×22﹣2(2π﹣4)=8.
故选A.
【点评】此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.
7.将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
A. B. C. D.
【考点】圆锥的计算.
【分析】过O点作OC⊥AB,垂足为D,交⊙O于点C,由折叠的性质可知OD为半径的一半,而OA为半径,可求∠A=30°,同理可得∠B=30°,在△AOB中,由内角和定理求∠AOB,然后求得弧AB的长,利用弧长公式求得围成的圆锥的底面半径,最后利用勾股定理求得其高即可.
【解答】解:过O点作OC⊥AB,垂足为D,交⊙O于点C,
由折叠的性质可知,OD=OC=OA,
由此可得,在Rt△AOD中,∠A=30°,
同理可得∠B=30°,
在△AOB中,由内角和定理,
得∠AOB=180°﹣∠A﹣∠B=120°
∴弧AB的长为=2π
设围成的圆锥的底面半径为r,
则2πr=2π
∴r=1cm
∴圆锥的高为=2
故选A.
【点评】本题考查了垂径定理,折叠的性质,特殊直角三角形的判断.关键是由折叠的性质得出含30°的直角三角形.
8.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B.2πa C. D.3a
【考点】弧长的计算.
【分析】由图可知,阴影部分的周长是两个圆心角为90°、半径为a的扇形的弧长,可据此求出阴影部分的周长.
【解答】解:∵四边形ABCD是边长为a正方形,
∴∠B=∠D=90°,AB=CB=AD=CD=a,
∴树叶形图案的周长=×2=πa.
故选A.
【点评】本题考查了弧长的计算.解答该题时,需要牢记弧长公式l=(R是半径).
二、填空题(共4小题,每小题3分,满分12分)
9.如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 48 度.
【考点】垂径定理.
【专题】几何图形问题.
【分析】根据点D是弦AC的中点,得到OD⊥AC,然后根据∠DOC=∠DOA即可求得答案.
【解答】解:∵AB是⊙O的直径,
∴OA=OC
∵∠A=42°
∴∠ACO=∠A=42°
∵D为AC的中点,
∴OD⊥AC,
∴∠DOC=90°﹣∠DCO=90°﹣42°=48°.
故答案为:48.
【点评】本题考查了垂径定理的知识,解题的关键是根的弦的中点得到弦的垂线.
10.如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
【考点】旋转的性质;弧长的计算.
【分析】根据Rt△ABC中的30°角所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半以及旋转的性质推知△AA′C是等边三角形,所以根据等边三角形的性质利用弧长公式来求CA′旋转所构成的扇形的弧长.
【解答】解:∵在Rt△ABC中,∠B=30°,AB=10cm,
∴AC=AB=5cm.
根据旋转的性质知,A′C=AC,
∴A′C=AB=5cm,
∴点A′是斜边AB的中点,
∴AA′=AB=5cm,
∴AA′=A′C=AC,
∴∠A′CA=60°,
∴CA′旋转所构成的扇形的弧长为: =(cm).
故答案是:.
【点评】本题考查了弧长的计算、旋转的性质.解题的难点是推知点A′是斜边AB的中点,同时,这也是解题的关键.
11.已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 25 cm.
【考点】圆锥的计算.
【分析】首先利用扇形的弧长公式求得扇形的弧长,然后利用圆的周长公式即可求解.
【解答】解:扇形的弧长是: =50πcm,
设底面半径是rcm,则2πr=50π,
解得:r=25.
故答案是:25.
【点评】考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
12.如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为 4π .
【考点】正方形的性质;整式的混合运算.
【专题】压轴题.
【分析】设正方形EFGB的边长为a,表示出CE、AG,然后根据阴影部分的面积=S扇形ABC+S正方形EFGB+S△CEF﹣S△AGF,列式计算即可得解.
【解答】解:设正方形EFGB的边长为a,则CE=4﹣a,AG=4+a,
阴影部分的面积=S扇形ABC+S正方形EFGB+S△CEF﹣S△AGF
=+a2+a(4﹣a)﹣a(4+a)
=4π+a2+2a﹣a2﹣2a﹣a2
=4π.
故答案为:4π.
【点评】本题考查了正方形的性质,整式的混合运算,扇形的面积计算,引入小正方形的边长这一中间量是解题的关键.
三、解答题(共3小题,满分0分)
13.(2013 威海)如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小;
(2)求阴影部分的面积.
【考点】垂径定理;圆心角、弧、弦的关系;扇形面积的计算.
【分析】(1)根据垂径定理可得=,∠C=∠AOD,然后在Rt△COE中可求出∠C的度数.
(2)连接OB,根据(1)可求出∠AOB=120°,在Rt△AOF中,求出AF,OF,然后根据S阴影=S扇形OAB﹣S△OAB,即可得出答案.
【解答】解:(1)∵CD是圆O的直径,CD⊥AB,
∴=,
∴∠C=∠AOD,
∵∠AOD=∠COE,
∴∠C=∠COE,
∵AO⊥BC,
∴∠C=30°.
(2)连接OB,
由(1)知,∠C=30°,
∴∠AOD=60°,
∴∠AOB=120°,
在Rt△AOF中,AO=1,∠AOF=60°,
∴AF=,OF=,
∴AB=,
∴S阴影=S扇形OADB﹣S△OAB=﹣××=π﹣.
【点评】本题考查了垂径定理及扇形的面积计算,解答本题的关键是利用解直角三角形的知识求出∠C、∠AOB的度数,难度一般.
14.(2013 聊城)如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=,BE=2.求证:
(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
【考点】切线的判定与性质;菱形的判定.
【专题】压轴题.
【分析】(1)首先连接OC,由垂径定理,可求得CE的长,又由勾股定理,可求得半径OC的长,然后由勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平行四边形,继而证得四边形FADC是菱形;
(2)首先连接OF,易证得△AFO≌△CFO,继而可证得FC是⊙O的切线.
【解答】证明:(1)连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=CD=×4=2,
设OC=x,
∵BE=2,
∴OE=x﹣2,
在Rt△OCE中,OC2=OE2+CE2,
∴x2=(x﹣2)2+(2)2,
解得:x=4,
∴OA=OC=4,OE=2,
∴AE=6,
在Rt△AED中,AD==4,
∴AD=CD,
∵AF是⊙O切线,
∴AF⊥AB,
∵CD⊥AB,
∴AF∥CD,
∵CF∥AD,
∴四边形FADC是平行四边形,
∵AD=CD,
∴平行四边形FADC是菱形;
(2)连接OF,AC,
∵四边形FADC是菱形,
∴FA=FC,
∴∠FAC=∠FCA,
∵AO=CO,
∴∠OAC=∠OCA,
∴∠FAC+∠OAC=∠FCA+∠OCA,
即∠OCF=∠OAF=90°,
即OC⊥FC,
∵点C在⊙O上,
∴FC是⊙O的切线.
【点评】此题考查了切线的判定与性质、菱形的判定与性质、垂径定理、勾股定理以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
15.(2013 莱芜)如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
【考点】圆的综合题.
【专题】压轴题.
【分析】(1)根据切线的判定得出∠PNO=∠PNM+∠ONA=∠AMO+∠ONA进而求出即可;
(2)根据已知得出∠PNM+∠ONA=90°,进而得出∠PNO=180°﹣90°=90°即可得出答案;
(3)首先根据外角的性质得出∠AON=30°进而利用扇形面积公式得出即可.
【解答】(1)PN与⊙O相切.
证明:连接ON,
则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°.
即PN与⊙O相切.
(2)成立.
证明:连接ON,
则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,
∵∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°.
∴∠PNO=180°﹣90°=90°.
即PN与⊙O相切.
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,
∴∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,
则NE=ON sin60°=1×=.
S阴影=S△AOC+S扇形AON﹣S△CON
=OC OA+CO NE
=×1×1+π﹣×1×
=+π﹣.
【点评】此题主要考查了扇形面积公式以及切线的判定等知识,熟练根据切线的判定得出对应角的度数是解题关键.
