4.2.2 两角和与差的正弦、正切公式及其应用 教案
文档属性
| 名称 | 4.2.2 两角和与差的正弦、正切公式及其应用 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 69.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览



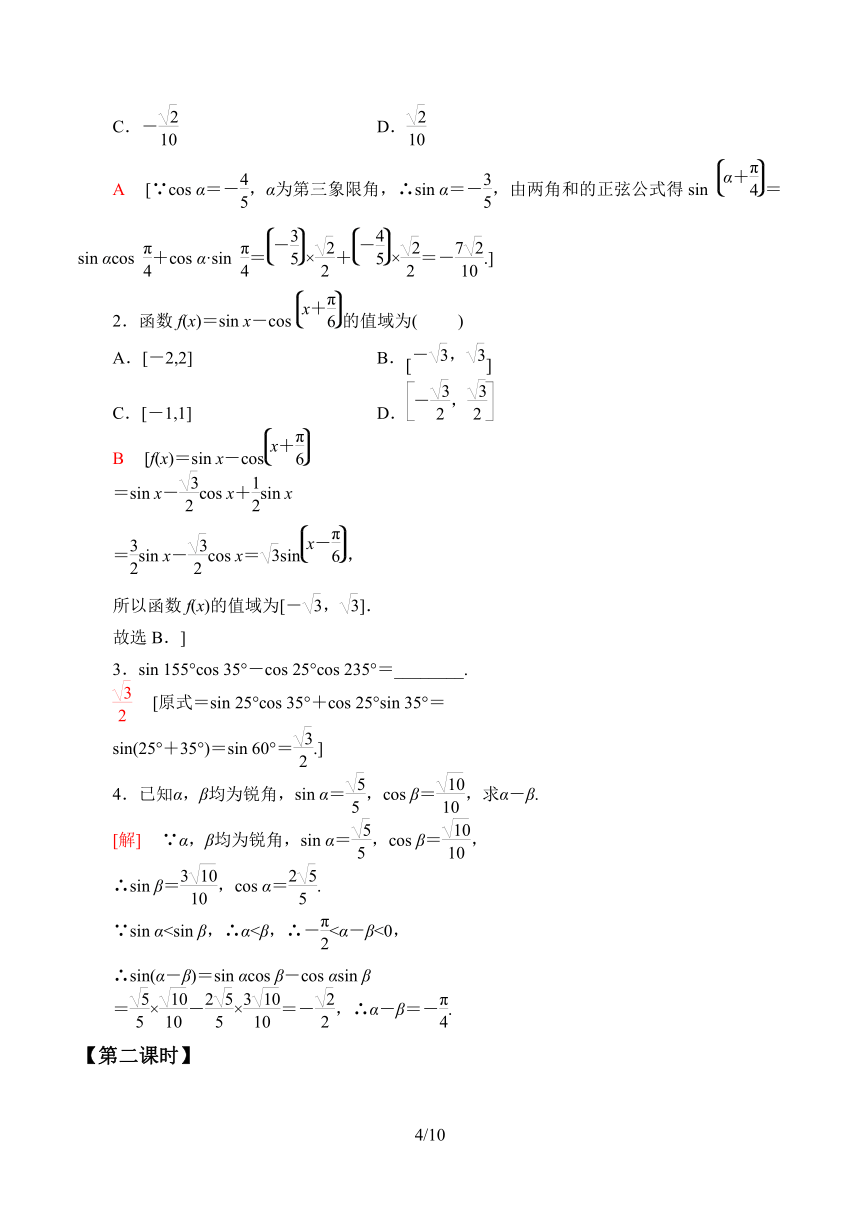

文档简介
两角和与差的正弦、正切公式及其应用
【第一课时】
【教学目标】
1.能利用两角和与差的余弦公式及诱导公式导出两角差的正弦公式、两角和的正弦公式.
2.能利用公式解决简单的化简求值问题.
【教学重难点】
利用两角和与差的正弦公式解决简单的化简求值问题.
【教学过程】
一、问题导入
怎样借助30°,45°的三角函数值求出sin75°,sin15°的值?
二、新知探究
1.利用公式化简求值
【例1】(1)=( )
A.- B.-
C. D.
(2)求sin 157°cos 67°+cos 23°sin 67°的值;
(3)求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值.
[思路探究](1)化简求值应注意公式的逆用.
(2)(3)对于非特殊角的三角函数式化简应转化为特殊角的三角函数值.
(1)C [
=
=
==sin 30°=.]
(2)解:原式=sin(180°-23°)cos 67°+cos 23°sin 67°
=sin 23°cos 67°+cos 23°sin 67°=sin(23°+67°)=sin 90°=1.
(3)sin(θ+75°)+cos(θ+45°)-cos(θ+15°)
=sin(θ+15°+60°)+cos(θ+15°+30°)-cos(θ+15°)
=sin(θ+15°)cos 60°+cos(θ+15°)sin 60°+cos(θ+15°)·
cos 30°-sin(θ+15°)sin 30°-cos(θ+15°)
=sin(θ+15°)+cos(θ+15°)+cos(θ+15°)-sin(θ+15°)-cos(θ+15°)=0.
【教师小结】
(一)对于非特殊角的三角函数式,要想利用两角和与差的正弦、余弦公式求出具体数值,一般有以下三种途径:
(1)化为特殊角的三角函数值;
(2)化为正负相消的项,消去,求值;
(3)化为分子、分母形式,进行约分再求值.
(二)在进行求值过程的变换中,一定要本着先整体后局部的基本原则,先整体分析三角函数式的特点,如果整体符合三角公式,则整体变形,否则进行各局部的变换.
2.给值(式)求值
【例2】设α∈,β∈,若cos α=-,sin β=-,求sin(α+β)的值.
[思路探究]应用公式 注意角的范围 求出所给角的正弦值.
[解]因为α∈,cos α=-,所以sin α=,因为β∈,sin β=-,所以cos β=.
所以sin(α+β)=sin αcos β+cos αsin β
=×+×=.
1.(变结论)若条件不变,试求sin(α-β)+cos(α-β)的值.
[解] sin(α-β)+cos(α-β)=sin αcos β-cos αsin β+cos αcos β+sin αsin β=×-×+×+×=---=-1.
2.(变条件)若将角β的条件改为第三象限,其他条件不变,则结果如何?
[解] 因为α∈,cos α=-,所以sin α=.
因为β为第三象限,所以cos β=-.
所以sin(α+β)=sin αcos β+cos αsin β=×+×=-+=0.
【教师小结】
(1)当“已知角”有两个或多个时,“所求角”一般可以表示为其中两个“已知角”的和或差的形式.
(2)当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.
(3)角的拆分方法不唯一,可根据题目合理选择拆分方式.
提醒:解题时要重视角的范围对三角函数值的制约,从而恰当、准确地求出三角函数值.
三、课堂总结
1.两角和与差的正弦公式的结构特点
(1)公式中的α,β均为任意角.
(2)两角和与差的正弦公式可以看成是诱导公式的推广,诱导公式可以看成是两角和与差的正弦公式的特例.
(3)两角和与差的正弦公式结构是“正余余正,加减相同”,两角和与差的余弦公式结构是“余余正正,加减相反”.
2.两角和与差的正弦、余弦公式的内在联系
3.使用和差公式时不仅要会正用,还要能够逆用公式.
四、课堂检测
1.若cos α=-,α是第三象限的角,则sin=( )
A.- B.
C.- D.
A [∵cos α=-,α为第三象限角,∴sin α=-,由两角和的正弦公式得sin =sin αcos +cos α·sin =×+×=-.]
2.函数f(x)=sin x-cos的值域为( )
A.[-2,2] B.
C.[-1,1] D.
B [f(x)=sin x-cos
=sin x-cos x+sin x
=sin x-cos x=sin,
所以函数f(x)的值域为[-,].
故选B.]
3.sin 155°cos 35°-cos 25°cos 235°=________.
[原式=sin 25°cos 35°+cos 25°sin 35°=
sin(25°+35°)=sin 60°=.]
4.已知α,β均为锐角,sin α=,cos β=,求α-β.
[解] ∵α,β均为锐角,sin α=,cos β=,
∴sin β=,cos α=.
∵sin α∴sin(α-β)=sin αcos β-cos αsin β
=×-×=-,∴α-β=-.
【第二课时】
【教学目标】
1.能利用两角和与差的余弦公式、正弦公式推导出两角和与差的正切公式.
2.掌握两角和与差的正切公式的变形使用,能利用公式进行简单的求值、化简等.
【教学重难点】
利用两角和与差的正弦公式解决简单的化简求值问题.
【教学过程】
一、问题导入
怎样借助30°,45°的三角函数值求出tan75°,tan15°的值?
二、新知探究
1.利用公式化简求值
【例1】求下列各式的值:
(1)tan 15°;(2);
(3)tan 23°+tan 37°+tan 23°tan 37°.
[思路探究]把非特殊角转化为特殊角(如(1))及公式的逆用(如(2))与活用(如(3)),通过适当的变形变为可以使用公式的形式,从而达到化简或求值的目的.
[解](1)tan 15°=tan(45°-30°)
====2-.
(2)=
=
=tan(30°-75°)=tan(-45°)=-tan 45°=-1.
(3)∵tan(23°+37°)=tan 60°==,
∴tan 23°+tan 37°=(1-tan 23°tan 37°),
∴原式=(1-tan 23°tan 37°)+tan 23°tan 37°=.
【教师小结】
(1)公式Tα+β,Tα-β是变形较多的两个公式,公式中有tan αtan β,tan α+tan β(或tan α-tan β),tan(α+β)(或tan(α-β)).三者知二可表示或求出第三个.
(2)一方面要熟记公式的结构,另一方面要注意常值代换.
2.条件求值(角)问题
【例2】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为,.
(1)求tan(α+β)的值;(2)求α+2β的值.
[思路探究]先由任意角的三角函数定义求出cos α,cos β,再求sin α,sin β,从而求出tan α,tan β,然后利用Tα+β求tan(α+β),最后利用α+2β=(α+β)+β,求tan(α+2β)进而得到α+2β的值.
[解]由条件得
cos α=,cos β=,
∵α,β为锐角,
∴sin α=,sin β=,
∴tan α=7,tan β=.
(1)tan(α+β)===-3.
(2)tan(α+2β)=tan[(α+β)+β]
===-1,
∵α,β为锐角,∴0<α+2β<,∴α+2β=.
【教师小结】
(一)通过先求角的某个三角函数值来求角.
(二)选取函数时,应遵照以下原则:
(1)已知正切函数值,选正切函数;
(2)已知正、余弦函数值,选正弦或余弦函数.若角的范围是,选正、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为,选正弦较好.
(三)给值求角的一般步骤:
(1)求角的某一三角函数值;
(2)确定角的范围;
(3)根据角的范围写出所求的角.
3.公式的变形应用
[探究问题]
(1)判断三角形的形状时,都有哪些特殊三角形?
[提示]根据三角形的边角关系,常见的特殊三角形有等边三角形、等腰三角形、锐角三角形、直角三角形、钝角三角形等.
(2)在△ABC中,tan(A+B)与tan C有何关系?
[提示]根据三角形内角和定理可得A+B+C=π,
∴A+B=π-C,
∴tan(A+B)=tan(π-C)=-tan C.
【例3】已知△ABC中,tan B+tan C+tan Btan C=,且tan A+tan B+1=tan Atan B,判断△ABC的形状.
[思路探究]→→
→.
[解]由tan A=tan[π-(B+C)]
=-tan(B+C)
===-.
而0°<A<180°,
∴A=120°.
由tan C=tan[π-(A+B)]=
==,
而0°<C<180°,
∴C=30°,
∴B=30°.
∴△ABC是顶角为120°的等腰三角形.
(变条件)例题中把条件改为“tan B+tan C-tan Btan C=-,且tan A+tan B+1=tan Atan B”,结果如何?
[解] 由tan A=tan [π-(B+C)]
=-tan (B+C)=
==.
又0°由tan C=tan [π-(A+B)]
===.
又0°所以C=60°,所以B=60°.
所以△ABC是等边三角形.
【教师小结】
公式Tα+β的逆用及变形应用的解题策略
(1)“1”的代换:在Tα+β中,如果分子中出现“1”常利用
1=tan 45°来代换,以达到化简求值的目的,
如=tan ;
=tan .
(2)整体意识:若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体,常考虑tan(α±β)的变形公式.
三、课堂总结
1.公式T(α±β)的适用范围和结构特征
(1)由正切函数的定义可知α、β、α+β(或α-β)的终边不能落在y轴上,即不为kπ+(k∈Z).
(2)公式T(α±β)的右侧为分式形式,其中分子为tan α与tan β的和或差,分母为1与tan αtan β的差或和.
2.两角和与差的正切公式的变形
变形公式如:tan α+tan β=tan(α+β)(1-tan α tan β);
tan α-tan β=tan(α-β)(1+tan α tan β);
tan α tan β=1-等.
四、课堂检测
1.设角θ的终边过点(2,3),则tan=( )
A. B.-
C.5 D.-5
A [由于角θ的终边过点(2,3),因此tan θ=,故tan===,选A.]
2.tan 10°tan 20°+(tan 10°+tan 20°)等于( )
A. B.1
C. D.
B [原式=tan 10°tan 20°+tan 30°(1-tan 10°tan 20°)=tan 10°tan 20°+1-tan 10°tan 20°=1.]
3.计算=________.
1 [=
=tan 45°=1.]
4.已知tan(α+β)=,tan=,求tan的值.
[解] ∵α+=(α+β)-,
∴tan=tan
==
=.
4/10
【第一课时】
【教学目标】
1.能利用两角和与差的余弦公式及诱导公式导出两角差的正弦公式、两角和的正弦公式.
2.能利用公式解决简单的化简求值问题.
【教学重难点】
利用两角和与差的正弦公式解决简单的化简求值问题.
【教学过程】
一、问题导入
怎样借助30°,45°的三角函数值求出sin75°,sin15°的值?
二、新知探究
1.利用公式化简求值
【例1】(1)=( )
A.- B.-
C. D.
(2)求sin 157°cos 67°+cos 23°sin 67°的值;
(3)求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值.
[思路探究](1)化简求值应注意公式的逆用.
(2)(3)对于非特殊角的三角函数式化简应转化为特殊角的三角函数值.
(1)C [
=
=
==sin 30°=.]
(2)解:原式=sin(180°-23°)cos 67°+cos 23°sin 67°
=sin 23°cos 67°+cos 23°sin 67°=sin(23°+67°)=sin 90°=1.
(3)sin(θ+75°)+cos(θ+45°)-cos(θ+15°)
=sin(θ+15°+60°)+cos(θ+15°+30°)-cos(θ+15°)
=sin(θ+15°)cos 60°+cos(θ+15°)sin 60°+cos(θ+15°)·
cos 30°-sin(θ+15°)sin 30°-cos(θ+15°)
=sin(θ+15°)+cos(θ+15°)+cos(θ+15°)-sin(θ+15°)-cos(θ+15°)=0.
【教师小结】
(一)对于非特殊角的三角函数式,要想利用两角和与差的正弦、余弦公式求出具体数值,一般有以下三种途径:
(1)化为特殊角的三角函数值;
(2)化为正负相消的项,消去,求值;
(3)化为分子、分母形式,进行约分再求值.
(二)在进行求值过程的变换中,一定要本着先整体后局部的基本原则,先整体分析三角函数式的特点,如果整体符合三角公式,则整体变形,否则进行各局部的变换.
2.给值(式)求值
【例2】设α∈,β∈,若cos α=-,sin β=-,求sin(α+β)的值.
[思路探究]应用公式 注意角的范围 求出所给角的正弦值.
[解]因为α∈,cos α=-,所以sin α=,因为β∈,sin β=-,所以cos β=.
所以sin(α+β)=sin αcos β+cos αsin β
=×+×=.
1.(变结论)若条件不变,试求sin(α-β)+cos(α-β)的值.
[解] sin(α-β)+cos(α-β)=sin αcos β-cos αsin β+cos αcos β+sin αsin β=×-×+×+×=---=-1.
2.(变条件)若将角β的条件改为第三象限,其他条件不变,则结果如何?
[解] 因为α∈,cos α=-,所以sin α=.
因为β为第三象限,所以cos β=-.
所以sin(α+β)=sin αcos β+cos αsin β=×+×=-+=0.
【教师小结】
(1)当“已知角”有两个或多个时,“所求角”一般可以表示为其中两个“已知角”的和或差的形式.
(2)当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.
(3)角的拆分方法不唯一,可根据题目合理选择拆分方式.
提醒:解题时要重视角的范围对三角函数值的制约,从而恰当、准确地求出三角函数值.
三、课堂总结
1.两角和与差的正弦公式的结构特点
(1)公式中的α,β均为任意角.
(2)两角和与差的正弦公式可以看成是诱导公式的推广,诱导公式可以看成是两角和与差的正弦公式的特例.
(3)两角和与差的正弦公式结构是“正余余正,加减相同”,两角和与差的余弦公式结构是“余余正正,加减相反”.
2.两角和与差的正弦、余弦公式的内在联系
3.使用和差公式时不仅要会正用,还要能够逆用公式.
四、课堂检测
1.若cos α=-,α是第三象限的角,则sin=( )
A.- B.
C.- D.
A [∵cos α=-,α为第三象限角,∴sin α=-,由两角和的正弦公式得sin =sin αcos +cos α·sin =×+×=-.]
2.函数f(x)=sin x-cos的值域为( )
A.[-2,2] B.
C.[-1,1] D.
B [f(x)=sin x-cos
=sin x-cos x+sin x
=sin x-cos x=sin,
所以函数f(x)的值域为[-,].
故选B.]
3.sin 155°cos 35°-cos 25°cos 235°=________.
[原式=sin 25°cos 35°+cos 25°sin 35°=
sin(25°+35°)=sin 60°=.]
4.已知α,β均为锐角,sin α=,cos β=,求α-β.
[解] ∵α,β均为锐角,sin α=,cos β=,
∴sin β=,cos α=.
∵sin α
=×-×=-,∴α-β=-.
【第二课时】
【教学目标】
1.能利用两角和与差的余弦公式、正弦公式推导出两角和与差的正切公式.
2.掌握两角和与差的正切公式的变形使用,能利用公式进行简单的求值、化简等.
【教学重难点】
利用两角和与差的正弦公式解决简单的化简求值问题.
【教学过程】
一、问题导入
怎样借助30°,45°的三角函数值求出tan75°,tan15°的值?
二、新知探究
1.利用公式化简求值
【例1】求下列各式的值:
(1)tan 15°;(2);
(3)tan 23°+tan 37°+tan 23°tan 37°.
[思路探究]把非特殊角转化为特殊角(如(1))及公式的逆用(如(2))与活用(如(3)),通过适当的变形变为可以使用公式的形式,从而达到化简或求值的目的.
[解](1)tan 15°=tan(45°-30°)
====2-.
(2)=
=
=tan(30°-75°)=tan(-45°)=-tan 45°=-1.
(3)∵tan(23°+37°)=tan 60°==,
∴tan 23°+tan 37°=(1-tan 23°tan 37°),
∴原式=(1-tan 23°tan 37°)+tan 23°tan 37°=.
【教师小结】
(1)公式Tα+β,Tα-β是变形较多的两个公式,公式中有tan αtan β,tan α+tan β(或tan α-tan β),tan(α+β)(或tan(α-β)).三者知二可表示或求出第三个.
(2)一方面要熟记公式的结构,另一方面要注意常值代换.
2.条件求值(角)问题
【例2】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为,.
(1)求tan(α+β)的值;(2)求α+2β的值.
[思路探究]先由任意角的三角函数定义求出cos α,cos β,再求sin α,sin β,从而求出tan α,tan β,然后利用Tα+β求tan(α+β),最后利用α+2β=(α+β)+β,求tan(α+2β)进而得到α+2β的值.
[解]由条件得
cos α=,cos β=,
∵α,β为锐角,
∴sin α=,sin β=,
∴tan α=7,tan β=.
(1)tan(α+β)===-3.
(2)tan(α+2β)=tan[(α+β)+β]
===-1,
∵α,β为锐角,∴0<α+2β<,∴α+2β=.
【教师小结】
(一)通过先求角的某个三角函数值来求角.
(二)选取函数时,应遵照以下原则:
(1)已知正切函数值,选正切函数;
(2)已知正、余弦函数值,选正弦或余弦函数.若角的范围是,选正、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为,选正弦较好.
(三)给值求角的一般步骤:
(1)求角的某一三角函数值;
(2)确定角的范围;
(3)根据角的范围写出所求的角.
3.公式的变形应用
[探究问题]
(1)判断三角形的形状时,都有哪些特殊三角形?
[提示]根据三角形的边角关系,常见的特殊三角形有等边三角形、等腰三角形、锐角三角形、直角三角形、钝角三角形等.
(2)在△ABC中,tan(A+B)与tan C有何关系?
[提示]根据三角形内角和定理可得A+B+C=π,
∴A+B=π-C,
∴tan(A+B)=tan(π-C)=-tan C.
【例3】已知△ABC中,tan B+tan C+tan Btan C=,且tan A+tan B+1=tan Atan B,判断△ABC的形状.
[思路探究]→→
→.
[解]由tan A=tan[π-(B+C)]
=-tan(B+C)
===-.
而0°<A<180°,
∴A=120°.
由tan C=tan[π-(A+B)]=
==,
而0°<C<180°,
∴C=30°,
∴B=30°.
∴△ABC是顶角为120°的等腰三角形.
(变条件)例题中把条件改为“tan B+tan C-tan Btan C=-,且tan A+tan B+1=tan Atan B”,结果如何?
[解] 由tan A=tan [π-(B+C)]
=-tan (B+C)=
==.
又0°
===.
又0°
所以△ABC是等边三角形.
【教师小结】
公式Tα+β的逆用及变形应用的解题策略
(1)“1”的代换:在Tα+β中,如果分子中出现“1”常利用
1=tan 45°来代换,以达到化简求值的目的,
如=tan ;
=tan .
(2)整体意识:若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体,常考虑tan(α±β)的变形公式.
三、课堂总结
1.公式T(α±β)的适用范围和结构特征
(1)由正切函数的定义可知α、β、α+β(或α-β)的终边不能落在y轴上,即不为kπ+(k∈Z).
(2)公式T(α±β)的右侧为分式形式,其中分子为tan α与tan β的和或差,分母为1与tan αtan β的差或和.
2.两角和与差的正切公式的变形
变形公式如:tan α+tan β=tan(α+β)(1-tan α tan β);
tan α-tan β=tan(α-β)(1+tan α tan β);
tan α tan β=1-等.
四、课堂检测
1.设角θ的终边过点(2,3),则tan=( )
A. B.-
C.5 D.-5
A [由于角θ的终边过点(2,3),因此tan θ=,故tan===,选A.]
2.tan 10°tan 20°+(tan 10°+tan 20°)等于( )
A. B.1
C. D.
B [原式=tan 10°tan 20°+tan 30°(1-tan 10°tan 20°)=tan 10°tan 20°+1-tan 10°tan 20°=1.]
3.计算=________.
1 [=
=tan 45°=1.]
4.已知tan(α+β)=,tan=,求tan的值.
[解] ∵α+=(α+β)-,
∴tan=tan
==
=.
4/10
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
