华师大版七年级数学下册6.2 第5课时 一元一次方程的应用
文档属性
| 名称 | 华师大版七年级数学下册6.2 第5课时 一元一次方程的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 726.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-10 11:29:22 | ||
图片预览








文档简介
课件21张PPT。一元一次方程的应用黔江区舟白中学典例解:根据一元一次方程的定义,得3a-5=1。解得a=2
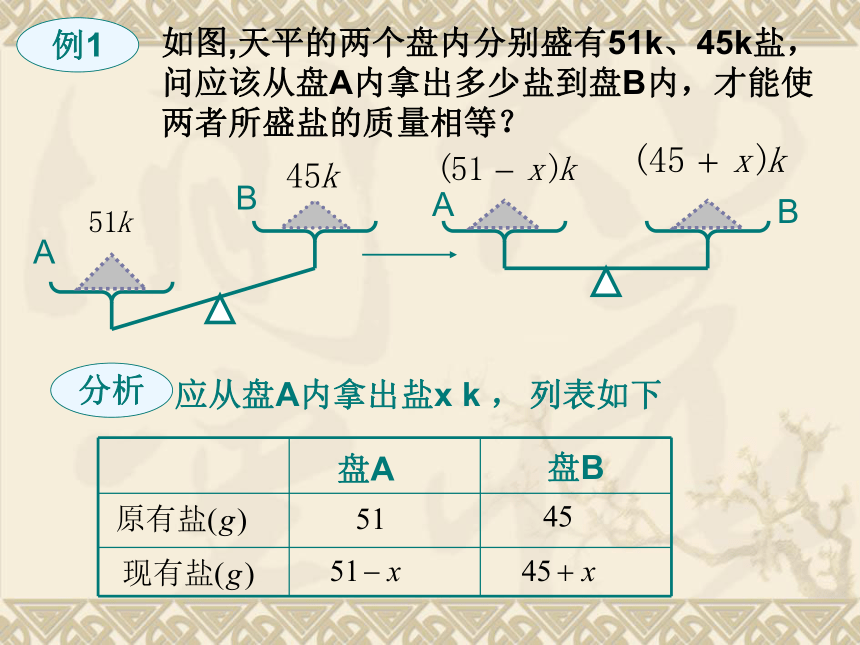
答:当a=2时,已知的等式是关于x的一元一次方程。(1)利用一元一次方程的定义构造。评析:一元一次方程的定义要求只含有一个未知数,并且未知数的次数为1,故有3a-5=1,从而求得a值。典例(2)利用一元一次方程解的定义构造。评析:利用方程解的定义知x=2满足所给的方程,代入方程后得到一个关于a的方程,解这个方程求得a的值,从而求出2a-1的值。讲解点1:列一元一次方程解题列一元一次方程解题,就是根据已知的条件,列出一个一元一次方程,通过求方程的解达到解决问题的目的。列方程的关键是抓住问题中有关数量的相等关系,即找到一个包含题目含义的数量关系。整个思维过程为:解:(1)某数的5倍加上3等于某数的7倍减去5;(3)某数的一半加上4,比某数的3倍小21;根据下列条件列出方程,然后求出某数(2)某数的3倍减去9等于某数的1/3加上6;(2)、(3)两题请同学们自己解。讲解点2:列一元一次方程解答实际问题列方程解答实际问题,关键是抓住问题中有关数量的相等关系,求得方程的解后,经过检验,就可得到实际问题的解答。列方程解应用题的步骤如下:(1)审题。弄清题意,找出已知量、未知量。(2)设未知数。对所求的未知量用设未知数表示。(3)列方程。根据题中的等量关系列出方程。(4)解方程。解所列的方程。(5)检验解。检验解出的未知数值是否符合题意。(6)答题。回答题中的问题。简记为:“审”、“设”、“列”、“解”、“验”、“答”注意:(1)设未知数时,要说清楚所设未知数表示的是什么,同时还要写清楚计算单位;(2)答题时要回答清楚题中所问的问题,同时写清楚计算单位。例1如图,天平的两个盘内分别盛有51k、45k盐,问应该从盘A内拿出多少盐到盘B内,才能使两者所盛盐的质量相等?分析应从盘A内拿出盐x k ,列表如下盘A盘BABAB解:=典例1、一桶油连桶重量为8千克,油用去一半后,连桶重量为4.5千克,桶内原来有油多少千克?解:设桶内原来有油x千克,由题意得
解得 x=7答:桶内原来有油7千克。引例学校团委组织65名团员为学校建花坛搬砖.初一同学每人搬6块,其他年级同学每人搬8块,总共搬了400块.问初一同学有多少人参加了搬砖?分析设:初一同学有 人参加了搬砖,列表如下初一学生其他年级学生总数参加人数每人搬砖数共搬砖数6540068解:例2学校团委组织65名新团员为学校建花坛搬砖.女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块.问这些新团员中有多少名男同学?分析设:新团员中有 名男同学,列表如下男同学女同学总数参加人数每人共搬砖数共搬砖数6518008×46×4解:归纳用方程解实际问题的过程:问题方程解答分析抽象求解检验分析和抽象的过程包括:(1)弄清题意,设未知数;(2)找相等关系;(3)列方程.练习(课本第11页)第1题1.学校田径队的小刚在400米跑测试时,先以6米/秒的速度跑完了大部分路程,最后以8米/秒的速度冲刺到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了多少时间?4006865设小刚在冲刺阶段花了 秒时间,由题意得﹢=400解:小刚在冲刺阶段花了 秒时间,由题意得﹢=400答:小刚在冲刺阶段花了 5 秒时间.做一做 足球的表面是由一些呈多边形的黑、白皮块缝而成的,共计有32块,已知黑色皮块比白色皮块数的一半多2,问两种皮块各有多少?解:设黑色皮块有 块,则白色皮块有 块 , 由题意得即黑色白色解得答:黑色皮块有 12 块,则白色皮块有20 块.习题(课本第12页)第4、5、6题5.小莉和同学在假期去森林公园玩,在溪流边的码头A地租了一艘小艇,逆流而上,划行速度约4千米/时.到B地后沿原路返回,速度增加了50﹪,回到A码头比去时少花了20分种.求A、B两地之间的路程.44(1+ 50﹪)即6设A、B两地之间的路程为 千米,由题意得-3千米(x- 3)千米8元收费1.2(x-3)元6.某市的出租车计价规则如下:行程不超过3千米,收起步价8元;超过部分每千米路程收费1.20元.某天李老师和三位学生去探望一位病假的学生,坐出租车付了17.60元,他们共乘坐了多少路程?解:设共乘坐了 千米的 路程,由题意得2、一个三位数,三个数位上数字的和是17,百位上的数字比十位上的数字大7,个位上的数字是十位上的数字的3倍。求这个三位数。解:设十位上的数字为x,则百位上的数字为(x+7)个位上的数字为3x。由题意得x + 7 + x + 3x = 17则百位上的数字为x+7=9,个位上的数字为3x=6,故所求的三位数为926。答:这个三位数为926。解得 x=2.作业
答:当a=2时,已知的等式是关于x的一元一次方程。(1)利用一元一次方程的定义构造。评析:一元一次方程的定义要求只含有一个未知数,并且未知数的次数为1,故有3a-5=1,从而求得a值。典例(2)利用一元一次方程解的定义构造。评析:利用方程解的定义知x=2满足所给的方程,代入方程后得到一个关于a的方程,解这个方程求得a的值,从而求出2a-1的值。讲解点1:列一元一次方程解题列一元一次方程解题,就是根据已知的条件,列出一个一元一次方程,通过求方程的解达到解决问题的目的。列方程的关键是抓住问题中有关数量的相等关系,即找到一个包含题目含义的数量关系。整个思维过程为:解:(1)某数的5倍加上3等于某数的7倍减去5;(3)某数的一半加上4,比某数的3倍小21;根据下列条件列出方程,然后求出某数(2)某数的3倍减去9等于某数的1/3加上6;(2)、(3)两题请同学们自己解。讲解点2:列一元一次方程解答实际问题列方程解答实际问题,关键是抓住问题中有关数量的相等关系,求得方程的解后,经过检验,就可得到实际问题的解答。列方程解应用题的步骤如下:(1)审题。弄清题意,找出已知量、未知量。(2)设未知数。对所求的未知量用设未知数表示。(3)列方程。根据题中的等量关系列出方程。(4)解方程。解所列的方程。(5)检验解。检验解出的未知数值是否符合题意。(6)答题。回答题中的问题。简记为:“审”、“设”、“列”、“解”、“验”、“答”注意:(1)设未知数时,要说清楚所设未知数表示的是什么,同时还要写清楚计算单位;(2)答题时要回答清楚题中所问的问题,同时写清楚计算单位。例1如图,天平的两个盘内分别盛有51k、45k盐,问应该从盘A内拿出多少盐到盘B内,才能使两者所盛盐的质量相等?分析应从盘A内拿出盐x k ,列表如下盘A盘BABAB解:=典例1、一桶油连桶重量为8千克,油用去一半后,连桶重量为4.5千克,桶内原来有油多少千克?解:设桶内原来有油x千克,由题意得
解得 x=7答:桶内原来有油7千克。引例学校团委组织65名团员为学校建花坛搬砖.初一同学每人搬6块,其他年级同学每人搬8块,总共搬了400块.问初一同学有多少人参加了搬砖?分析设:初一同学有 人参加了搬砖,列表如下初一学生其他年级学生总数参加人数每人搬砖数共搬砖数6540068解:例2学校团委组织65名新团员为学校建花坛搬砖.女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块.问这些新团员中有多少名男同学?分析设:新团员中有 名男同学,列表如下男同学女同学总数参加人数每人共搬砖数共搬砖数6518008×46×4解:归纳用方程解实际问题的过程:问题方程解答分析抽象求解检验分析和抽象的过程包括:(1)弄清题意,设未知数;(2)找相等关系;(3)列方程.练习(课本第11页)第1题1.学校田径队的小刚在400米跑测试时,先以6米/秒的速度跑完了大部分路程,最后以8米/秒的速度冲刺到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了多少时间?4006865设小刚在冲刺阶段花了 秒时间,由题意得﹢=400解:小刚在冲刺阶段花了 秒时间,由题意得﹢=400答:小刚在冲刺阶段花了 5 秒时间.做一做 足球的表面是由一些呈多边形的黑、白皮块缝而成的,共计有32块,已知黑色皮块比白色皮块数的一半多2,问两种皮块各有多少?解:设黑色皮块有 块,则白色皮块有 块 , 由题意得即黑色白色解得答:黑色皮块有 12 块,则白色皮块有20 块.习题(课本第12页)第4、5、6题5.小莉和同学在假期去森林公园玩,在溪流边的码头A地租了一艘小艇,逆流而上,划行速度约4千米/时.到B地后沿原路返回,速度增加了50﹪,回到A码头比去时少花了20分种.求A、B两地之间的路程.44(1+ 50﹪)即6设A、B两地之间的路程为 千米,由题意得-3千米(x- 3)千米8元收费1.2(x-3)元6.某市的出租车计价规则如下:行程不超过3千米,收起步价8元;超过部分每千米路程收费1.20元.某天李老师和三位学生去探望一位病假的学生,坐出租车付了17.60元,他们共乘坐了多少路程?解:设共乘坐了 千米的 路程,由题意得2、一个三位数,三个数位上数字的和是17,百位上的数字比十位上的数字大7,个位上的数字是十位上的数字的3倍。求这个三位数。解:设十位上的数字为x,则百位上的数字为(x+7)个位上的数字为3x。由题意得x + 7 + x + 3x = 17则百位上的数字为x+7=9,个位上的数字为3x=6,故所求的三位数为926。答:这个三位数为926。解得 x=2.作业
