沪科版数学七年级下册 6.2 实数 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 6.2 实数 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 313.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
6.2 实数
1、实数可以这样
分类:
2、实数也可以
这样分类:
实数
_____实数
_____
_____实数
有理
无理
正有理
负有理
有限小数或无限循环小数
实数
______数
________数
_______________________________________
________数
0
______数 _________数
________数
___________________________________________
正无理
负无理
无限不循环小数
正
0
负
有理数和无理数统称为
实数
复习巩固
1、若无理数a满足:1<a<4,请写出两个你熟
悉的无理数:_____,______.
2、判断下列说法是否正确:
(1)带根号的数是无理数;( )
(2)不带根号的数一定是有理数;( )
(3)负数没有立方根;( )
(4)-
是17的平方根.( )
×
×
×
√
小练习
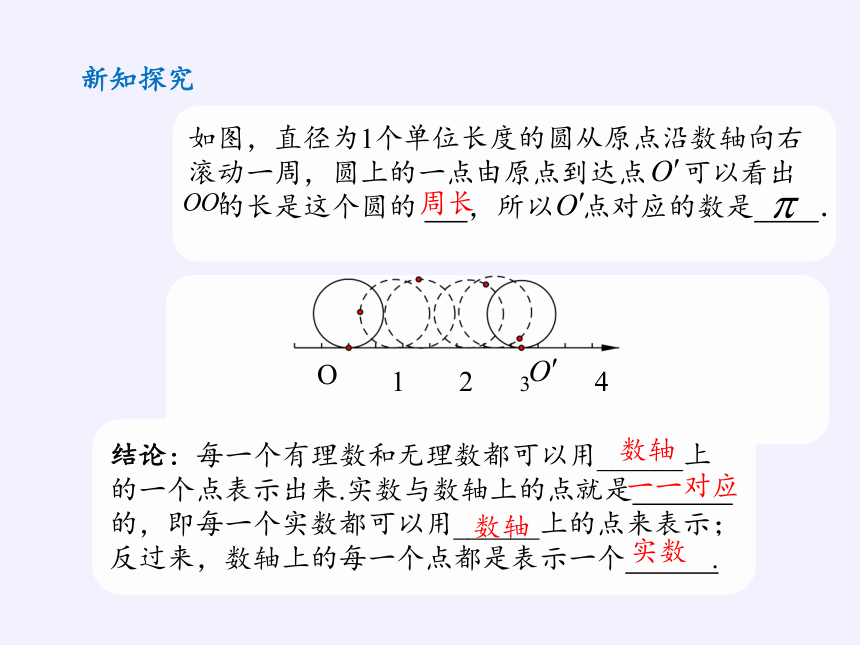
结论:每一个有理数和无理数都可以用______上
的一个点表示出来.实数与数轴上的点就是
的,即每一个实数都可以用______上的点来表示;
反过来,数轴上的每一个点都是表示一个 .
如图,直径为1个单位长度的圆从原点沿数轴向右
滚动一周,圆上的一点由原点到达点 可以看出
的长是这个圆的 ,所以 点对应的数是 .
O
1
2
3
4
周长
数轴
一一对应
数轴
实数
新知探究
练一练
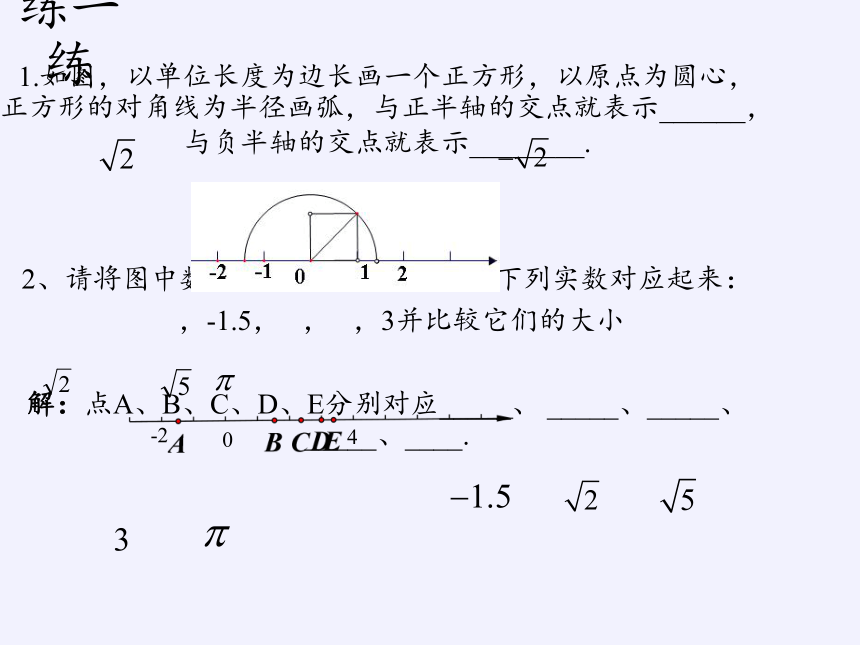
1.如图,以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧,与正半轴的交点就表示______,与负半轴的交点就表示________.
2、请将图中数轴上标有字母的各点与下列实数对应起来:
,-1.5, , ,3并比较它们的大小
解:点A、B、C、D、E分别对应_____、 _____、_____、_____、____.
0
-2
4
3
实数中相反数和绝对值的意义
思考:
的相反数是___.-π的相反数是____.0的相反数是____;
∣ ∣=____,∣-π∣= ____
∣0∣=____.
讲授新课
结论:有理数关于相反数和绝对值的意义同样适合于实数:
1、数a的相反数是____,这里a表示任意一个______.
2、一个正实数的绝对值________;一个负实数的绝对值是________;0的绝对值是 ____.即:
-a
实数
它本身
它的相反数
0
a
0
-a
例1:
(1)分别写出 , 的相反数;
(2)指出 分别是什么数的相反数;
知识应用
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
1、填表(求出下列各数的相反数与绝对值):
2、求下列各式中的实数x。
巩固训练
例1 计算:(结果保留小数点后两位):
2.236
3.142
5.38
1.732
1.414
2.45
温馨提示:计算的过程一般比要求保留的小数点位数多一位.
练一练 计算(结果精确到0.01):
实数的运算
例2、计算下列各式的值:
温馨提示:在进行实数的运算时,有理数的运算法则及运算性质等同样适用.
练一练 计算:
课堂练习
大显身手
计算:
2、数a的相反数是____,这里表示任意一个______.
3、一个正实数的绝对值________;一个负实数的绝对值是_________;0的绝对值是 ____.即:
-a
实数
它本身
它的相反数
0
a
0
-a
课堂小结
1、实数与数轴上的点是 ___ 的.
一一对应
知识总结
4、在进行实数的运算时,有理数的_______及___________等同样适用.
运算法则
运算律
5、学习反思:
收获___________________反思__________________
能力提升
解:
因为2< <3,
所以x=2, y= -2
x(y+2)2=
2( -2+2) 2
=2( )2
=14
谢 谢
6.2 实数
1、实数可以这样
分类:
2、实数也可以
这样分类:
实数
_____实数
_____
_____实数
有理
无理
正有理
负有理
有限小数或无限循环小数
实数
______数
________数
_______________________________________
________数
0
______数 _________数
________数
___________________________________________
正无理
负无理
无限不循环小数
正
0
负
有理数和无理数统称为
实数
复习巩固
1、若无理数a满足:1<a<4,请写出两个你熟
悉的无理数:_____,______.
2、判断下列说法是否正确:
(1)带根号的数是无理数;( )
(2)不带根号的数一定是有理数;( )
(3)负数没有立方根;( )
(4)-
是17的平方根.( )
×
×
×
√
小练习
结论:每一个有理数和无理数都可以用______上
的一个点表示出来.实数与数轴上的点就是
的,即每一个实数都可以用______上的点来表示;
反过来,数轴上的每一个点都是表示一个 .
如图,直径为1个单位长度的圆从原点沿数轴向右
滚动一周,圆上的一点由原点到达点 可以看出
的长是这个圆的 ,所以 点对应的数是 .
O
1
2
3
4
周长
数轴
一一对应
数轴
实数
新知探究
练一练
1.如图,以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧,与正半轴的交点就表示______,与负半轴的交点就表示________.
2、请将图中数轴上标有字母的各点与下列实数对应起来:
,-1.5, , ,3并比较它们的大小
解:点A、B、C、D、E分别对应_____、 _____、_____、_____、____.
0
-2
4
3
实数中相反数和绝对值的意义
思考:
的相反数是___.-π的相反数是____.0的相反数是____;
∣ ∣=____,∣-π∣= ____
∣0∣=____.
讲授新课
结论:有理数关于相反数和绝对值的意义同样适合于实数:
1、数a的相反数是____,这里a表示任意一个______.
2、一个正实数的绝对值________;一个负实数的绝对值是________;0的绝对值是 ____.即:
-a
实数
它本身
它的相反数
0
a
0
-a
例1:
(1)分别写出 , 的相反数;
(2)指出 分别是什么数的相反数;
知识应用
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
1、填表(求出下列各数的相反数与绝对值):
2、求下列各式中的实数x。
巩固训练
例1 计算:(结果保留小数点后两位):
2.236
3.142
5.38
1.732
1.414
2.45
温馨提示:计算的过程一般比要求保留的小数点位数多一位.
练一练 计算(结果精确到0.01):
实数的运算
例2、计算下列各式的值:
温馨提示:在进行实数的运算时,有理数的运算法则及运算性质等同样适用.
练一练 计算:
课堂练习
大显身手
计算:
2、数a的相反数是____,这里表示任意一个______.
3、一个正实数的绝对值________;一个负实数的绝对值是_________;0的绝对值是 ____.即:
-a
实数
它本身
它的相反数
0
a
0
-a
课堂小结
1、实数与数轴上的点是 ___ 的.
一一对应
知识总结
4、在进行实数的运算时,有理数的_______及___________等同样适用.
运算法则
运算律
5、学习反思:
收获___________________反思__________________
能力提升
解:
因为2< <3,
所以x=2, y= -2
x(y+2)2=
2( -2+2) 2
=2( )2
=14
谢 谢
