沪科版数学七年级下册 8.1 同底数幂的乘法 课件(共19张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.1 同底数幂的乘法 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 293.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 14:10:50 | ||
图片预览



文档简介
(共20张PPT)
8.1 幂的运算
--同底数幂的乘法
知识回顾
1.an 表示的意义是什么?其中a、n、an分别叫做什么
an
底数
幂
指数
an = a × a × a ×… a
n个a
2、填一填
1、在23中,3是________,2是_______,幂是________;
2、根据乘方的意义:(-2)3 表示____个 ____ 相乘,等于 _______;
(-3)4 表示 ____ 个 ____ 相乘,等于_______;
指数
底数
23
3
-2
4
-3
- 8
81
探索新知
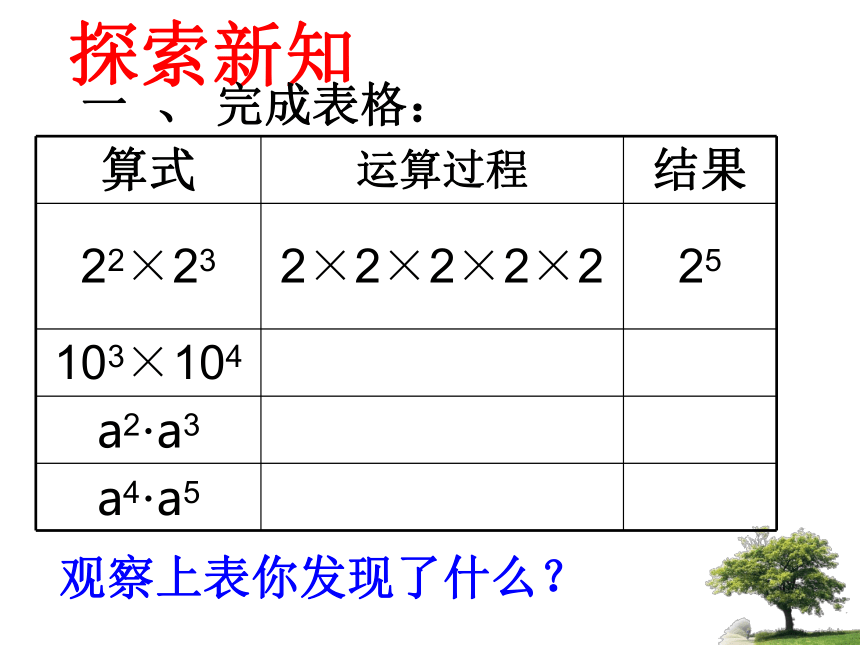
一 、 完成表格:
算式 运算过程 结果
22×23 2×2×2×2×2 25
103×104
a2·a3
a4·a5
观察上表你发现了什么?
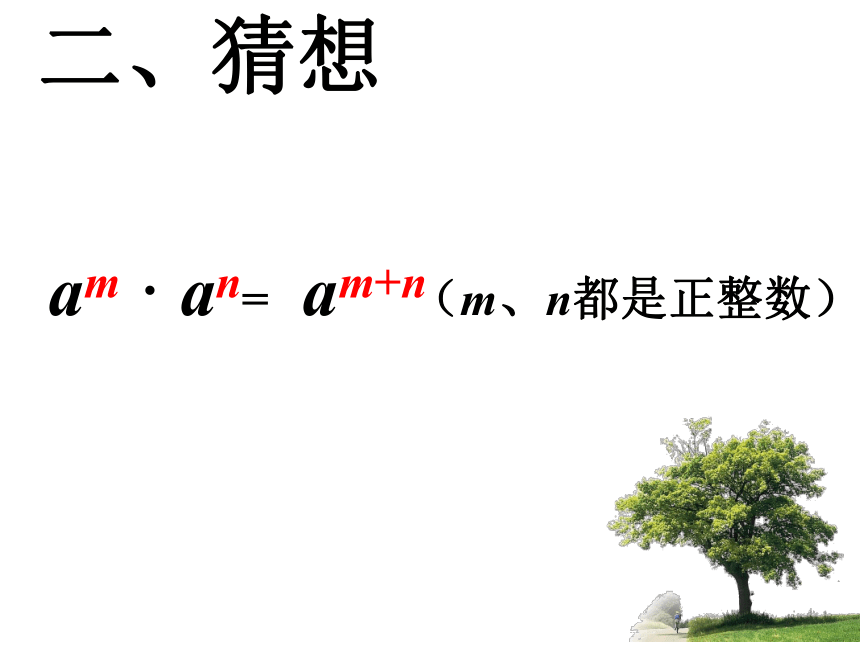
am · an= (m、n都是正整数)
am+n
二、猜想
2、根据猜想你能直接写出以下各式的结果吗?
(1)1012×108;
(2)
(3)a5 · a12
am · an= (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n(m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
二、验证猜想
同底数幂的乘法性质:
am · an = am+n (m、n都是正整数)
同底数幂相乘:
底数 ,指数 .
不变
相加
如 43×45=
43+5
=48
运算形式:
运算方法:
同底、乘法
底不变、指相加
小试牛刀
易错辨析
下面计算对不对?如果不对,应怎样改正?
(1)a a2=a2
(2)b3 b3=2b3
(3)m2+m2=m4
(4)(m+n)3 (m+n)5=(m+n)15
(5) (-2)3X23 =26
(6)m + m3 = m4
知识剖析
1、指数是“1”时,不要误认为没有指数。
2、底数a可以是一个数字或字母,也可以是一个单项式或多项式。
3、当底数是互为相反数时,要先变
为同底数幂后再运算。
例1、计算
沙场点兵
P46
1、下面的计算对不对?如果不对,应怎样改正?
3、教材
(1)x3 + x3=x6
(2)x3 x3=2x3
(3)c c3=c3
(4)c+c3=c4
2、计算
(1)105×103 (2)-a2.a5
(3)- x3·(-x)5 (4)y8·(-y )
(5)(- x)2 ·x3 (- x)3 (6)(-y)2·(-y)3·(-y )
已知am=5,an=6,求am+n的值.
am·an =am+n (m、n都是正整数)反之亦成立,
即am+n = am · an .
知识拓展
课堂小结:
1、本节课我们学了哪些主要内容?
am · an = am+n (m、n都是正整数)
同底数幂相乘:
底数 ,指数 .
不变
相加
运算形式:
运算方法:
同底、乘法
底不变、指相加
布置作业:
P54 1
谢 谢
8.1 幂的运算
--同底数幂的乘法
知识回顾
1.an 表示的意义是什么?其中a、n、an分别叫做什么
an
底数
幂
指数
an = a × a × a ×… a
n个a
2、填一填
1、在23中,3是________,2是_______,幂是________;
2、根据乘方的意义:(-2)3 表示____个 ____ 相乘,等于 _______;
(-3)4 表示 ____ 个 ____ 相乘,等于_______;
指数
底数
23
3
-2
4
-3
- 8
81
探索新知
一 、 完成表格:
算式 运算过程 结果
22×23 2×2×2×2×2 25
103×104
a2·a3
a4·a5
观察上表你发现了什么?
am · an= (m、n都是正整数)
am+n
二、猜想
2、根据猜想你能直接写出以下各式的结果吗?
(1)1012×108;
(2)
(3)a5 · a12
am · an= (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n(m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
二、验证猜想
同底数幂的乘法性质:
am · an = am+n (m、n都是正整数)
同底数幂相乘:
底数 ,指数 .
不变
相加
如 43×45=
43+5
=48
运算形式:
运算方法:
同底、乘法
底不变、指相加
小试牛刀
易错辨析
下面计算对不对?如果不对,应怎样改正?
(1)a a2=a2
(2)b3 b3=2b3
(3)m2+m2=m4
(4)(m+n)3 (m+n)5=(m+n)15
(5) (-2)3X23 =26
(6)m + m3 = m4
知识剖析
1、指数是“1”时,不要误认为没有指数。
2、底数a可以是一个数字或字母,也可以是一个单项式或多项式。
3、当底数是互为相反数时,要先变
为同底数幂后再运算。
例1、计算
沙场点兵
P46
1、下面的计算对不对?如果不对,应怎样改正?
3、教材
(1)x3 + x3=x6
(2)x3 x3=2x3
(3)c c3=c3
(4)c+c3=c4
2、计算
(1)105×103 (2)-a2.a5
(3)- x3·(-x)5 (4)y8·(-y )
(5)(- x)2 ·x3 (- x)3 (6)(-y)2·(-y)3·(-y )
已知am=5,an=6,求am+n的值.
am·an =am+n (m、n都是正整数)反之亦成立,
即am+n = am · an .
知识拓展
课堂小结:
1、本节课我们学了哪些主要内容?
am · an = am+n (m、n都是正整数)
同底数幂相乘:
底数 ,指数 .
不变
相加
运算形式:
运算方法:
同底、乘法
底不变、指相加
布置作业:
P54 1
谢 谢
