沪科版数学七年级下册 8.3 完全平方公式与平方差公式 课件(共32张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.3 完全平方公式与平方差公式 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
8.3 完全平方公式与平方差公式
多项式与多项式相乘的法则
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加。
(a+b)(m+n)=am+an+bm+bn
(a+b)2=
a2+
ab
+
b2
2
回 顾
自主实验
①现有两个数,不知其大小,请你随意用两个不同的字母来表示这两个数。
②请把这两个数的和与差分别表示出来,这两个式子是多项式还是单项式?
③请将所得的和与差相乘并化简。
④请思考:两个数的和与这两个数的差的乘积等于什么?
两数和
两数差
两数平方差
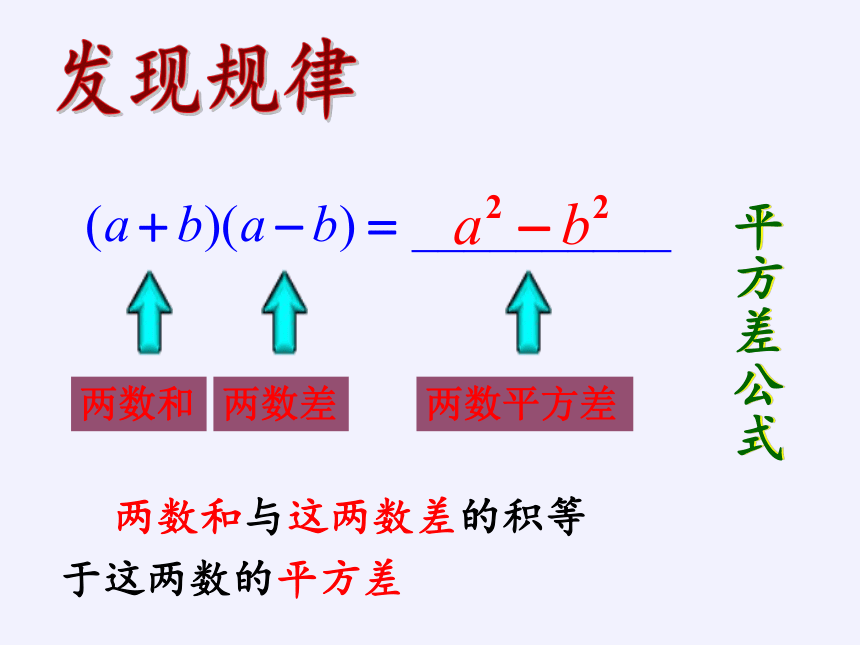
两数和与这两数差的积等于这两数的平方差
平方差公式
发现规律
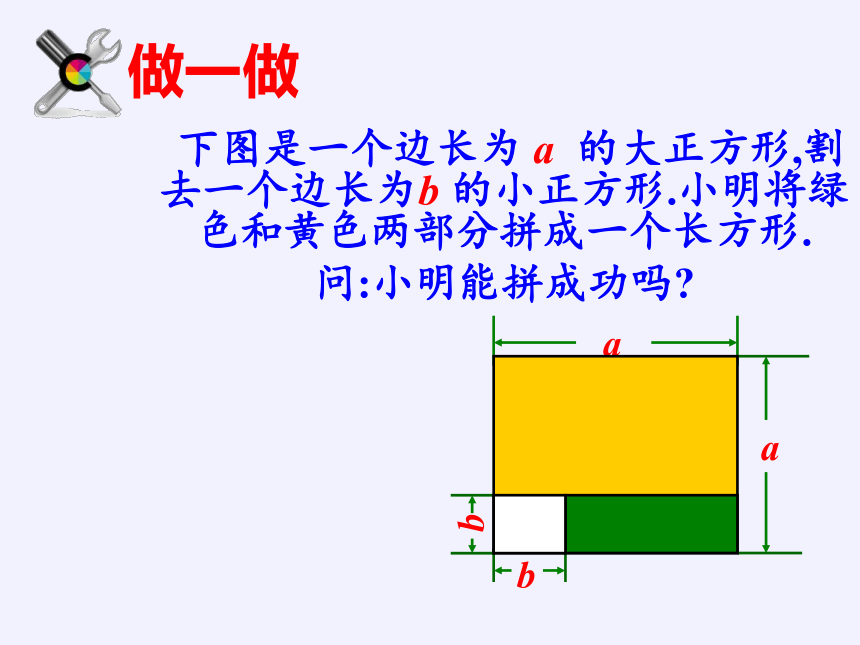
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗
做一做
b
a
a
b
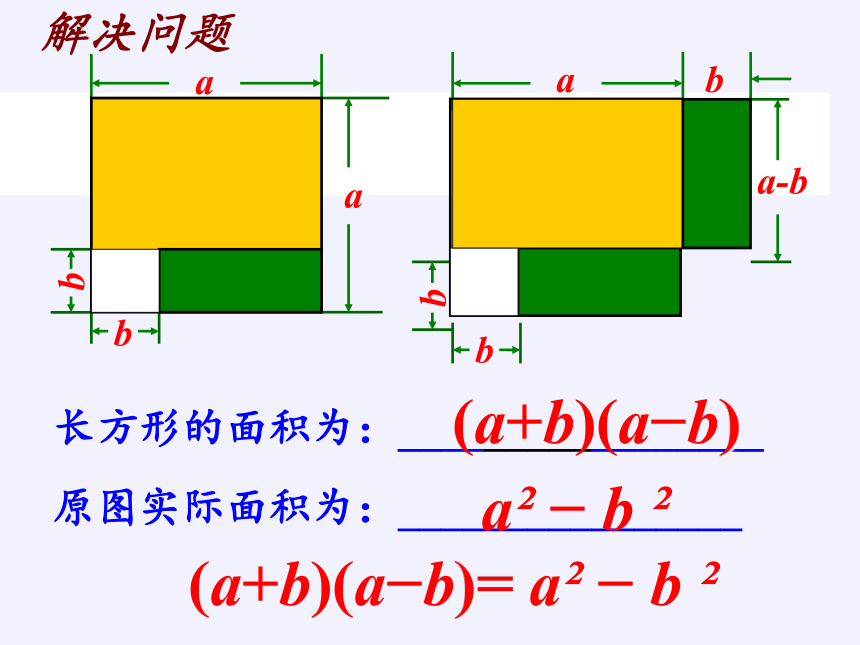
原图实际面积为:________________
长方形的面积为:_________________
b
a
a
b
a-b
b
b
a
b
解决问题
(a+b)(a b)
(a+b)(a b)= a b
a b
b
a
a
b
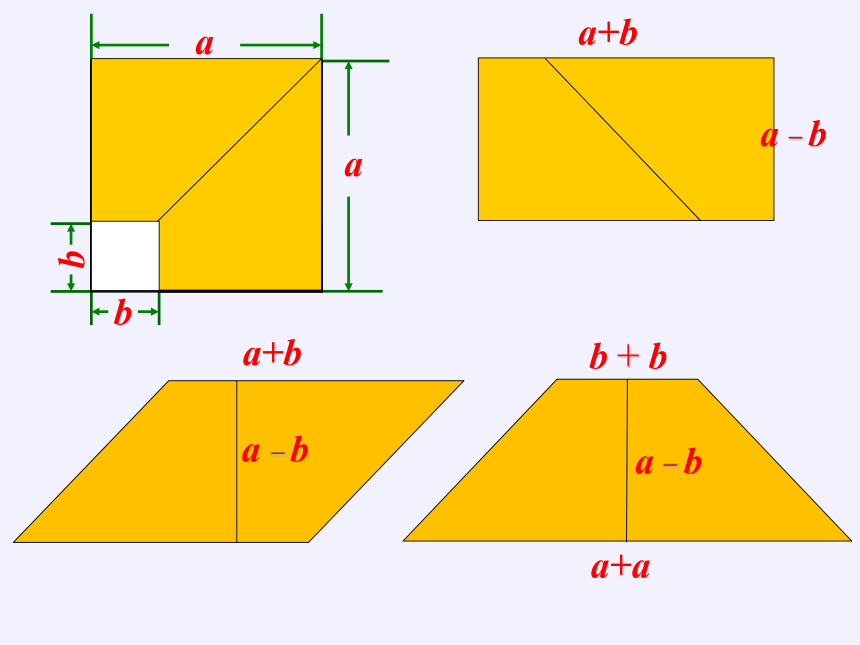
a+b
a b
a+b
a b
b + b
a+a
a b
平方差公式:
(a+b)(a b)=
a2 b2
两数和与这两数差的积,
等于
这两数的平方差.
公式变形:
a a
b b
a a
1、(a b)(a+b) =
a2 b2
2、( b+ a)(b+a) =
a2 b2
b b
a a
b b
公式的结构特征
(1)左边是两个二项式相乘,这两项中有一项完全相同,另一项互为相反项。
(2)右边是乘式中两项的平方差(相同项的平方减相反项的平方)。
(3)公式中的a、b可以表示数、字母、单项式或者多项式。
下列各式中能用平方差公式计算的是( )
A (– a + b ) (–a – b)
B (a –b ) (b –a)
C (100+8 ) ( 100 – 7)
D (x+y – 1 ) (x+y – 1)
选择
A
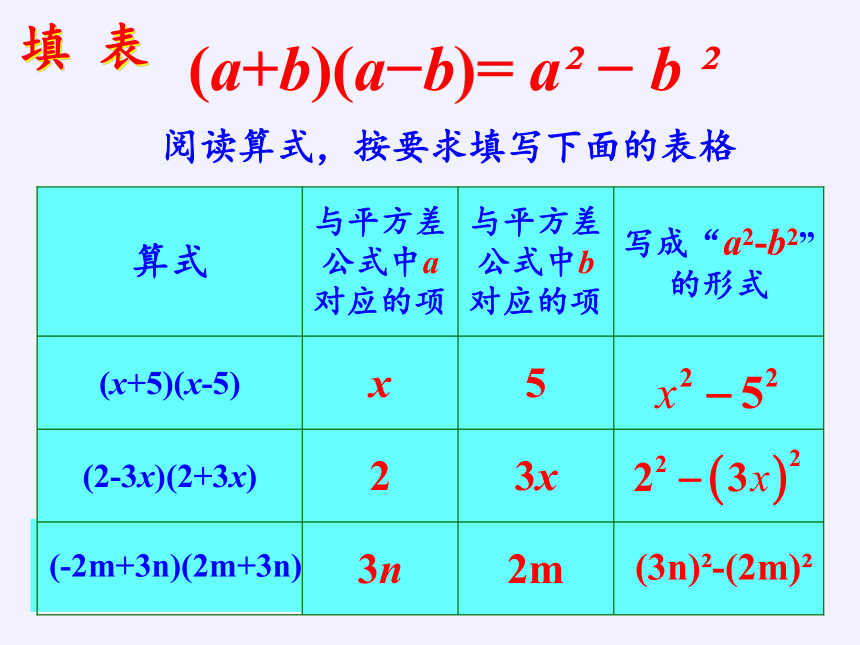
填 表
阅读算式,按要求填写下面的表格
2m
3n
(-2m+3n)(2m+3n)
3x
2
(2-3x)(2+3x)
5
x
(x+5)(x-5)
写成“a2-b2”的形式
与平方差公式中b对应的项
与平方差公式中a对应的项
算式
(3n) -(2m)
(a+b)(a b)= a b
例题
例 利用平方差公式计算:
(1) (5+6x)(5 6x);(2) (x+2y)(x 2y); (3) ( m+n)( m n).
解: (1) (5+6x)(5 6x)=
5
5
相同项
52
平方
6x
6x
相反项
平方
要用括号把这个数整个括起来,
注意
当“a或b”是一个分数或是数与字母的乘积时,
再平方;
( )2
6x
=
25
最后的结果又要去掉括号.
36x2 ;
(2) (x+2y) (x 2y)
=
x
x
x2
( )2
2y
2y
2y
=
x2 4y2 ;
(3) ( m+n)( m n )
=
m
m
m
( )2
n
n
n2
=
m2 n2 .
利用平方差计算的步骤
一、判断(是否符合平方差公式特征)
二、找项(找出相同项与相反项)
三、计算(相同项的平方减去相反项的平方)
归纳
下面各式的计算对不对?如果不对应当
怎样改正?
(1) (x+2)(x –2)=x –2
(2) (–3a –2)(3a –2)=9a –4
(3) (3m+2n)(3m –2n)=3m –2n
x – 4
4 – 9a
9m – 4n
判断
利用平方差公式计算
(1) (2a+5b)(2a-5b)
(2) (y –2x)(–2x –y)
(3) (y+2) (y –2)–(y –1) (y+5)
练习
小明同学去商店买了单价10.2元/千克的糖果9.8千克,小明同学马上说:“应付99.96元。”售货员很惊讶:“你真是个神童。”小明同学说:“过奖了 ,我只是利用了数学上刚学的一个公式而已。”
学以致用
10.2×9.8
=(10+0.2)×(10 –0.2)
=10 –0.2
=100 –0.04
=99.96
利用平方差公式计算:
(1)1999 ×2001
(2)2016 –2014×2018
平方差公式的
(1)结构是稳定不变的,即只要是两个数的和与这两个数差的乘积,就一定等于这两个数的平方差。
(2)公式中的a和b都可以变脸。
本质
位置变化
计算(–7n+2m)(2m+7n)
解:原式 = (2m–7n)(2m+7n)
=(2m) –(7n)
=4m –49n
变化一
系数变化
计算(4a+2b)(2a–b)
解:原式=2 (2a+b)(2a–b)
=2(4a –b )
=8a –2b
变化二
符号变化
计算:(–3a–4b)(3a–4b)
解:原式= (–4b–3a)(–4b+3a)
=(–4b) –(3a)
=16b –9a
变化三
指数变化
计算(x –y )(x +y )
解:原式=(x ) – (y )
=x4–y4
变化四
连用公式
计算(x+y)(x –y) (x +y )
解:原式= (x –y )(x +y )
=(x ) – (y )
=x4–y4
变化五
无中生有
计算51 ×49
解:原式=(50+1) ×(50 – 1)
=50 – 1
=2500 – 1
=2499
变化六
项数变化
计算(x+y+1)(x+y –1)
解:原式=(x+y) – 1
= x +2xy+y – 1
变化七
变化八
逆用公式
(a+b)(a b)
a2 b2 =
计算84 – 83
解:原式=(84+83) ×(84–83)
=167×1
=167
能力提升
利用平方差公式计算
( 2+1 )( 2 +1 )( 24+1 )( 28+1 )
( 2+1 )( 2 +1 )(24+1 )( 28+1 )
( 2 +1 )( 24+1 )( 28+1)
( 24+1 )( 28+1)
( 28+1 )
=216 – 1
挑战自我
解:原式
= ( 2 – 1 )
= ( 2 – 1 )
= ( 24 – 1 )
= ( 28 – 1)
拓展思考
想一想:
下列式子能用平方差公式计算吗?
(1)(x+2y–1)(x–2y+1)
(2)100 –99 +98 –97 +···+2 –1
“!”
“?”
“······”
作业布置
同步练习 8.3(二)
谢 谢
8.3 完全平方公式与平方差公式
多项式与多项式相乘的法则
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加。
(a+b)(m+n)=am+an+bm+bn
(a+b)2=
a2+
ab
+
b2
2
回 顾
自主实验
①现有两个数,不知其大小,请你随意用两个不同的字母来表示这两个数。
②请把这两个数的和与差分别表示出来,这两个式子是多项式还是单项式?
③请将所得的和与差相乘并化简。
④请思考:两个数的和与这两个数的差的乘积等于什么?
两数和
两数差
两数平方差
两数和与这两数差的积等于这两数的平方差
平方差公式
发现规律
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗
做一做
b
a
a
b
原图实际面积为:________________
长方形的面积为:_________________
b
a
a
b
a-b
b
b
a
b
解决问题
(a+b)(a b)
(a+b)(a b)= a b
a b
b
a
a
b
a+b
a b
a+b
a b
b + b
a+a
a b
平方差公式:
(a+b)(a b)=
a2 b2
两数和与这两数差的积,
等于
这两数的平方差.
公式变形:
a a
b b
a a
1、(a b)(a+b) =
a2 b2
2、( b+ a)(b+a) =
a2 b2
b b
a a
b b
公式的结构特征
(1)左边是两个二项式相乘,这两项中有一项完全相同,另一项互为相反项。
(2)右边是乘式中两项的平方差(相同项的平方减相反项的平方)。
(3)公式中的a、b可以表示数、字母、单项式或者多项式。
下列各式中能用平方差公式计算的是( )
A (– a + b ) (–a – b)
B (a –b ) (b –a)
C (100+8 ) ( 100 – 7)
D (x+y – 1 ) (x+y – 1)
选择
A
填 表
阅读算式,按要求填写下面的表格
2m
3n
(-2m+3n)(2m+3n)
3x
2
(2-3x)(2+3x)
5
x
(x+5)(x-5)
写成“a2-b2”的形式
与平方差公式中b对应的项
与平方差公式中a对应的项
算式
(3n) -(2m)
(a+b)(a b)= a b
例题
例 利用平方差公式计算:
(1) (5+6x)(5 6x);(2) (x+2y)(x 2y); (3) ( m+n)( m n).
解: (1) (5+6x)(5 6x)=
5
5
相同项
52
平方
6x
6x
相反项
平方
要用括号把这个数整个括起来,
注意
当“a或b”是一个分数或是数与字母的乘积时,
再平方;
( )2
6x
=
25
最后的结果又要去掉括号.
36x2 ;
(2) (x+2y) (x 2y)
=
x
x
x2
( )2
2y
2y
2y
=
x2 4y2 ;
(3) ( m+n)( m n )
=
m
m
m
( )2
n
n
n2
=
m2 n2 .
利用平方差计算的步骤
一、判断(是否符合平方差公式特征)
二、找项(找出相同项与相反项)
三、计算(相同项的平方减去相反项的平方)
归纳
下面各式的计算对不对?如果不对应当
怎样改正?
(1) (x+2)(x –2)=x –2
(2) (–3a –2)(3a –2)=9a –4
(3) (3m+2n)(3m –2n)=3m –2n
x – 4
4 – 9a
9m – 4n
判断
利用平方差公式计算
(1) (2a+5b)(2a-5b)
(2) (y –2x)(–2x –y)
(3) (y+2) (y –2)–(y –1) (y+5)
练习
小明同学去商店买了单价10.2元/千克的糖果9.8千克,小明同学马上说:“应付99.96元。”售货员很惊讶:“你真是个神童。”小明同学说:“过奖了 ,我只是利用了数学上刚学的一个公式而已。”
学以致用
10.2×9.8
=(10+0.2)×(10 –0.2)
=10 –0.2
=100 –0.04
=99.96
利用平方差公式计算:
(1)1999 ×2001
(2)2016 –2014×2018
平方差公式的
(1)结构是稳定不变的,即只要是两个数的和与这两个数差的乘积,就一定等于这两个数的平方差。
(2)公式中的a和b都可以变脸。
本质
位置变化
计算(–7n+2m)(2m+7n)
解:原式 = (2m–7n)(2m+7n)
=(2m) –(7n)
=4m –49n
变化一
系数变化
计算(4a+2b)(2a–b)
解:原式=2 (2a+b)(2a–b)
=2(4a –b )
=8a –2b
变化二
符号变化
计算:(–3a–4b)(3a–4b)
解:原式= (–4b–3a)(–4b+3a)
=(–4b) –(3a)
=16b –9a
变化三
指数变化
计算(x –y )(x +y )
解:原式=(x ) – (y )
=x4–y4
变化四
连用公式
计算(x+y)(x –y) (x +y )
解:原式= (x –y )(x +y )
=(x ) – (y )
=x4–y4
变化五
无中生有
计算51 ×49
解:原式=(50+1) ×(50 – 1)
=50 – 1
=2500 – 1
=2499
变化六
项数变化
计算(x+y+1)(x+y –1)
解:原式=(x+y) – 1
= x +2xy+y – 1
变化七
变化八
逆用公式
(a+b)(a b)
a2 b2 =
计算84 – 83
解:原式=(84+83) ×(84–83)
=167×1
=167
能力提升
利用平方差公式计算
( 2+1 )( 2 +1 )( 24+1 )( 28+1 )
( 2+1 )( 2 +1 )(24+1 )( 28+1 )
( 2 +1 )( 24+1 )( 28+1)
( 24+1 )( 28+1)
( 28+1 )
=216 – 1
挑战自我
解:原式
= ( 2 – 1 )
= ( 2 – 1 )
= ( 24 – 1 )
= ( 28 – 1)
拓展思考
想一想:
下列式子能用平方差公式计算吗?
(1)(x+2y–1)(x–2y+1)
(2)100 –99 +98 –97 +···+2 –1
“!”
“?”
“······”
作业布置
同步练习 8.3(二)
谢 谢
