第一章计数原理归纳整合 课件(人教A版选修2-3)
文档属性
| 名称 | 第一章计数原理归纳整合 课件(人教A版选修2-3) | 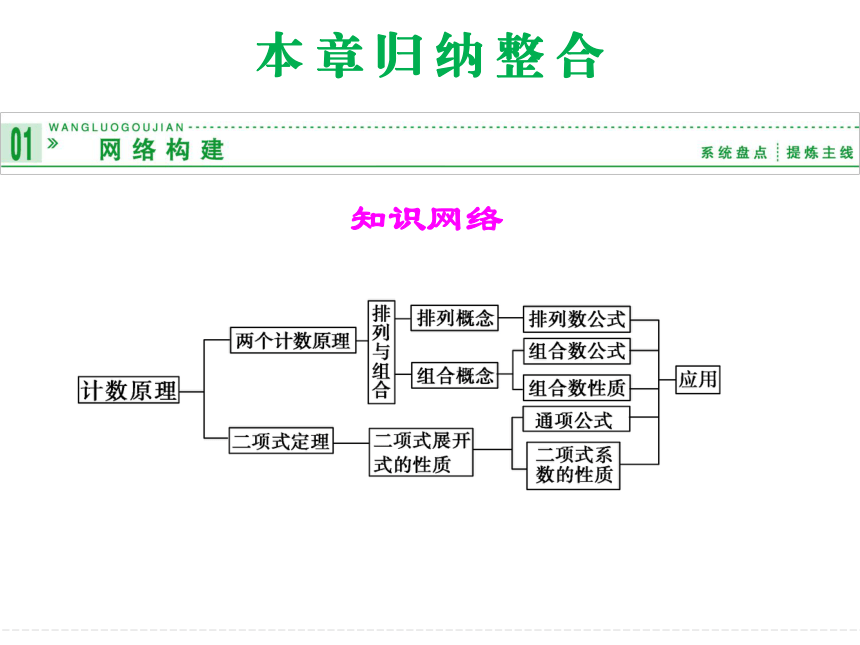 | |
| 格式 | zip | ||
| 文件大小 | 589.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-10 14:58:56 | ||
图片预览







文档简介
课件18张PPT。知识网络本 章 归 纳 整 合两个计数原理
分步乘法计数原理与分类加法计数原理是排列组合中解决问题的重要手段,也是基础方法,尤其是分类加法计数原理与分类讨论有很多相通之处,当遇到比较复杂的问题时,用分类的方法可以有效的将之分解,达到求解的目的.正确地分类与分步是用好两个原理的关键,即完成一件事到底是“分步”进行还是“分类”进行,这是选用计数原理的关键.注意有些复杂的问题往往在分步中有分类,分类中有分步,两个原理往往交错使用.要点归纳1.排列与组合
主要是排列数与组合数计算公式、性质的应用以及排列组合应用题.
排列数与组合数计算公式主要应用于求值和证明恒等式,其中求值问题应用连乘的形式,证明恒等式应用阶乘的形式,在证明恒等式时,要注意观察恒等式左右两边的形式,基本遵循由繁到简的原则,有时也会从两边向中间靠拢.
对于应用题,则首先要分清是否有序,即是排列问题还是组合问题.
有限制条件的排列问题,通常从以下两种途径考虑:(1)元素分析法:先考虑特殊元素的要求,再考虑其他元素.(2)位置分析法:先考虑特殊位置的要求,再考虑其他位置.
2.组合应用题的难点是与几何图形有关的问题,此时一般要与两个原理结合应用,还要结合图形的实际意义.
排列与组合综合应用题中也有很多重点和难点,比如分配问题,一般方法是先分组,后分配,分组问题又要注意均匀分组和不均匀分组的区别,均匀分组在各组逐一满足后还要除以均匀分组组数的全排列;而有公共元素的分配问题,则可以利用图示法求组数,这样可以避免分组中的重复.
二项式定理
这部分常考知识、题型、主要方法以及注意点大体如下:
(1)与二项式定理有关,包括定理的正向应用、逆向应用,题型如证明整除性、近似计算、证明一些简单的组合恒等式等,此时主要是要构造二项式,合理应用展开式;
3.(3)与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和,主要方法是赋值法,通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果,在求各项系数的绝对值的和时,则要先根据绝对值里面数的符号赋值求解.
专题一 两个计数原理选择使用两个原理解决问题时,要根据我们完成某件事情采取的方式而定,确定是分类还是分步要抓住两个原理的本质.分类加法计数原理的关键是“类”,分类时,首选要根据问题的特点确定一个合适的分类标准,然后在这个标准下进行分类;其次分类时要注意,完成这件事的任何一种方法必须属于某一类,并且分别属于不同类的两种方法必须属于某一类,并且分别属于不同类的两种方法是不同的方法.分步乘法计数原理的关键是“步”,分步时首先要根据问题的特点确定一个分步的标准;其次,分步时还要注意满足完成一件事必须并且只有连续完成这n个步骤后,这件事才算完成,只有满足了上述条件,才能用分步乘法计数原理. 有3封信,4个信筒.
(1)把3封信都寄出,有多少种寄信方法?
(2)把3封信都寄出,且每个信筒中最多一封信,有多少种寄信方法?
解 (1)分3步完成寄出3封信的任务;第一步,寄出1封信,有4种方法;第二步,再寄出1封信,有4种方法;第三步,寄出最后1封信,有4种方法,完成任务,根据分步乘法计数原理,共有4×4×4=43=64种寄信方法.【例1】排列组合应用题是高考的一个重点内容,常与实际问题相结合进行考查.要认真阅读题干,明确问题本质,利用排列组合的相关公式与方法解题.
(1)在求解排列与组合应用问题时,应注意:
①把具体问题转化或归结为排列或组合问题;
②通过分析确定运用分类计数原理还是分步计数原理;
③分析题目条件,避免“选取”时重复和遗漏;
④列出式子计算并作答.
(2)处理排列组合的综合性问题,一般思想方法是先选元素(组合),后排列,按元素的性质“分类”和按事件发生的连续过程
“分步”,始终是处理排列组合问题的基本方法和原理,通过专题二 排列组合的应用解题训练注意积累分类和分步的基本技能.
(3)解排列组合应用题时,常见的解题策略有以下几种:
①特殊元素优先安排的策略;
②合理分类和准确分步的策略;
③排列、组合混合问题先选后排的策略;
④正难则反、等价转化的策略;
⑤相邻问题捆绑处理的策略;
⑥不相邻问题插空处理的策略;
⑦定序问题除法处理的策略;
⑧分排问题直排处理的策略;
⑨“小集团”排列问题中先整体后局部的策略;
⑩构造模型的策略.
某运输公司有7个车队,每个车队的车均多于4辆,现从这个公司中抽调出10辆车,并且每个车队中至少抽取1辆车,那么共有多少种不同的抽调方式?
【例2】 (1)一条长椅上有9个座位,3个人坐,若相邻2人之间至少有2个空椅子,共有几种不同的坐法?
(2)一条长椅上有7个座位,4个人坐,要求3个空位中,恰有2个空位相邻,共有多少种不同的坐法?【例3】二项式定理是历年高考中的必考内容,解决二项式定理问题,特别是涉及求二项展开式的通项的问题,关键在于抓住通项公式,还要注意区分“二项式系数”与“展开式系数”.
二项式定理的应用主要有以下几个方面:
(1)近似求值.利用二项式定理进行近似计算,关键在于构造恰当的二项式(p+q)n(其中|q|<1),并根据近似要求,对展开式的项合理取舍.
(2)解决整除问题.通常把底数化为两数的和或差的形式,且这种转化形式与除数有密切的关系,再利用二项式定理展开,只考虑前面或后面的一两项就可以.
专题三 二项式定理及应用(3)求和.求二项展开式系数和的基本方法是赋值法.在解决有些数列求和的问题时,要注意对问题实施转化,为应用二项式定理创造条件.
(4)解不等式或证明组合恒等式.用二项式定理证明不等式时,通常表现为二项式定理的正用或逆用,再结合不等式的证明方法论证.而证明组合恒等式的关键在于构造不同的二项式,比较系数进行证明.
【例4】 若(3x-1)7=a7x7+a6x6+…+a1x+a0,
求(1)a1+a2+…+a7的值;
(2)a1+a3+a5+a7的值;
(3)a0+a2+a4+a6的值.
解 (1)令x=0,则a0=-1,令x=1,
则a7+a6+…+a1+a0=27=128 ①
所以a1+a2+…+a7=129;
(2)令x=-1,则
-a7+a6-a5+a4-a3+a2-a1+a0=(-4)7 ②,
【例5】 求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).
【例6】排列、组合试题从形式上看有以下几种最为常见的问题:数字问题,人或物的排列问题,几何问题,选代表或选样品的问题,集合的子集个数问题.试题的难度与教材习题相当,为体现高考的选拔功能,少数题有难度,多为几何问题.
二项式定理试题每年一道,题型为以下几种:求展开式中的某一项或某一项系数的问题;求所有项系数的和或者奇数项、偶数项系数和的问题;二项式某一项为字母,求这个字母的值的问题;求近似值的问题,试题难度不大,与教材习题相当.
命题趋势
分步乘法计数原理与分类加法计数原理是排列组合中解决问题的重要手段,也是基础方法,尤其是分类加法计数原理与分类讨论有很多相通之处,当遇到比较复杂的问题时,用分类的方法可以有效的将之分解,达到求解的目的.正确地分类与分步是用好两个原理的关键,即完成一件事到底是“分步”进行还是“分类”进行,这是选用计数原理的关键.注意有些复杂的问题往往在分步中有分类,分类中有分步,两个原理往往交错使用.要点归纳1.排列与组合
主要是排列数与组合数计算公式、性质的应用以及排列组合应用题.
排列数与组合数计算公式主要应用于求值和证明恒等式,其中求值问题应用连乘的形式,证明恒等式应用阶乘的形式,在证明恒等式时,要注意观察恒等式左右两边的形式,基本遵循由繁到简的原则,有时也会从两边向中间靠拢.
对于应用题,则首先要分清是否有序,即是排列问题还是组合问题.
有限制条件的排列问题,通常从以下两种途径考虑:(1)元素分析法:先考虑特殊元素的要求,再考虑其他元素.(2)位置分析法:先考虑特殊位置的要求,再考虑其他位置.
2.组合应用题的难点是与几何图形有关的问题,此时一般要与两个原理结合应用,还要结合图形的实际意义.
排列与组合综合应用题中也有很多重点和难点,比如分配问题,一般方法是先分组,后分配,分组问题又要注意均匀分组和不均匀分组的区别,均匀分组在各组逐一满足后还要除以均匀分组组数的全排列;而有公共元素的分配问题,则可以利用图示法求组数,这样可以避免分组中的重复.
二项式定理
这部分常考知识、题型、主要方法以及注意点大体如下:
(1)与二项式定理有关,包括定理的正向应用、逆向应用,题型如证明整除性、近似计算、证明一些简单的组合恒等式等,此时主要是要构造二项式,合理应用展开式;
3.(3)与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和,主要方法是赋值法,通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果,在求各项系数的绝对值的和时,则要先根据绝对值里面数的符号赋值求解.
专题一 两个计数原理选择使用两个原理解决问题时,要根据我们完成某件事情采取的方式而定,确定是分类还是分步要抓住两个原理的本质.分类加法计数原理的关键是“类”,分类时,首选要根据问题的特点确定一个合适的分类标准,然后在这个标准下进行分类;其次分类时要注意,完成这件事的任何一种方法必须属于某一类,并且分别属于不同类的两种方法必须属于某一类,并且分别属于不同类的两种方法是不同的方法.分步乘法计数原理的关键是“步”,分步时首先要根据问题的特点确定一个分步的标准;其次,分步时还要注意满足完成一件事必须并且只有连续完成这n个步骤后,这件事才算完成,只有满足了上述条件,才能用分步乘法计数原理. 有3封信,4个信筒.
(1)把3封信都寄出,有多少种寄信方法?
(2)把3封信都寄出,且每个信筒中最多一封信,有多少种寄信方法?
解 (1)分3步完成寄出3封信的任务;第一步,寄出1封信,有4种方法;第二步,再寄出1封信,有4种方法;第三步,寄出最后1封信,有4种方法,完成任务,根据分步乘法计数原理,共有4×4×4=43=64种寄信方法.【例1】排列组合应用题是高考的一个重点内容,常与实际问题相结合进行考查.要认真阅读题干,明确问题本质,利用排列组合的相关公式与方法解题.
(1)在求解排列与组合应用问题时,应注意:
①把具体问题转化或归结为排列或组合问题;
②通过分析确定运用分类计数原理还是分步计数原理;
③分析题目条件,避免“选取”时重复和遗漏;
④列出式子计算并作答.
(2)处理排列组合的综合性问题,一般思想方法是先选元素(组合),后排列,按元素的性质“分类”和按事件发生的连续过程
“分步”,始终是处理排列组合问题的基本方法和原理,通过专题二 排列组合的应用解题训练注意积累分类和分步的基本技能.
(3)解排列组合应用题时,常见的解题策略有以下几种:
①特殊元素优先安排的策略;
②合理分类和准确分步的策略;
③排列、组合混合问题先选后排的策略;
④正难则反、等价转化的策略;
⑤相邻问题捆绑处理的策略;
⑥不相邻问题插空处理的策略;
⑦定序问题除法处理的策略;
⑧分排问题直排处理的策略;
⑨“小集团”排列问题中先整体后局部的策略;
⑩构造模型的策略.
某运输公司有7个车队,每个车队的车均多于4辆,现从这个公司中抽调出10辆车,并且每个车队中至少抽取1辆车,那么共有多少种不同的抽调方式?
【例2】 (1)一条长椅上有9个座位,3个人坐,若相邻2人之间至少有2个空椅子,共有几种不同的坐法?
(2)一条长椅上有7个座位,4个人坐,要求3个空位中,恰有2个空位相邻,共有多少种不同的坐法?【例3】二项式定理是历年高考中的必考内容,解决二项式定理问题,特别是涉及求二项展开式的通项的问题,关键在于抓住通项公式,还要注意区分“二项式系数”与“展开式系数”.
二项式定理的应用主要有以下几个方面:
(1)近似求值.利用二项式定理进行近似计算,关键在于构造恰当的二项式(p+q)n(其中|q|<1),并根据近似要求,对展开式的项合理取舍.
(2)解决整除问题.通常把底数化为两数的和或差的形式,且这种转化形式与除数有密切的关系,再利用二项式定理展开,只考虑前面或后面的一两项就可以.
专题三 二项式定理及应用(3)求和.求二项展开式系数和的基本方法是赋值法.在解决有些数列求和的问题时,要注意对问题实施转化,为应用二项式定理创造条件.
(4)解不等式或证明组合恒等式.用二项式定理证明不等式时,通常表现为二项式定理的正用或逆用,再结合不等式的证明方法论证.而证明组合恒等式的关键在于构造不同的二项式,比较系数进行证明.
【例4】 若(3x-1)7=a7x7+a6x6+…+a1x+a0,
求(1)a1+a2+…+a7的值;
(2)a1+a3+a5+a7的值;
(3)a0+a2+a4+a6的值.
解 (1)令x=0,则a0=-1,令x=1,
则a7+a6+…+a1+a0=27=128 ①
所以a1+a2+…+a7=129;
(2)令x=-1,则
-a7+a6-a5+a4-a3+a2-a1+a0=(-4)7 ②,
【例5】 求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).
【例6】排列、组合试题从形式上看有以下几种最为常见的问题:数字问题,人或物的排列问题,几何问题,选代表或选样品的问题,集合的子集个数问题.试题的难度与教材习题相当,为体现高考的选拔功能,少数题有难度,多为几何问题.
二项式定理试题每年一道,题型为以下几种:求展开式中的某一项或某一项系数的问题;求所有项系数的和或者奇数项、偶数项系数和的问题;二项式某一项为字母,求这个字母的值的问题;求近似值的问题,试题难度不大,与教材习题相当.
命题趋势
