人教A版(2019)高中数学选择性必修第一册1.1.2空间向量的数量积(共26张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册1.1.2空间向量的数量积(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 15:46:06 | ||
图片预览







文档简介
(共26张PPT)
1.1.2空间向量的数量积运算
两个向量的夹角的定义
O
A
B
学习新知
两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]
(2)两个向量的数量积
注意: ①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
学习新知
不一定为锐角
不一定为钝角
巩固练习
空间向量的数量积性质
注意:
①性质2)是证明两向量垂直的依据;
②性质3)是求向量的长度(模)的依据;
③性质(5)是用来求两个向量的夹角
对于非零向量 ,有:
学习新知
空间向量的数量积满足的运算律
注意:
数量积不满足结合律即
学习新知
×
×
×
×
巩固练习
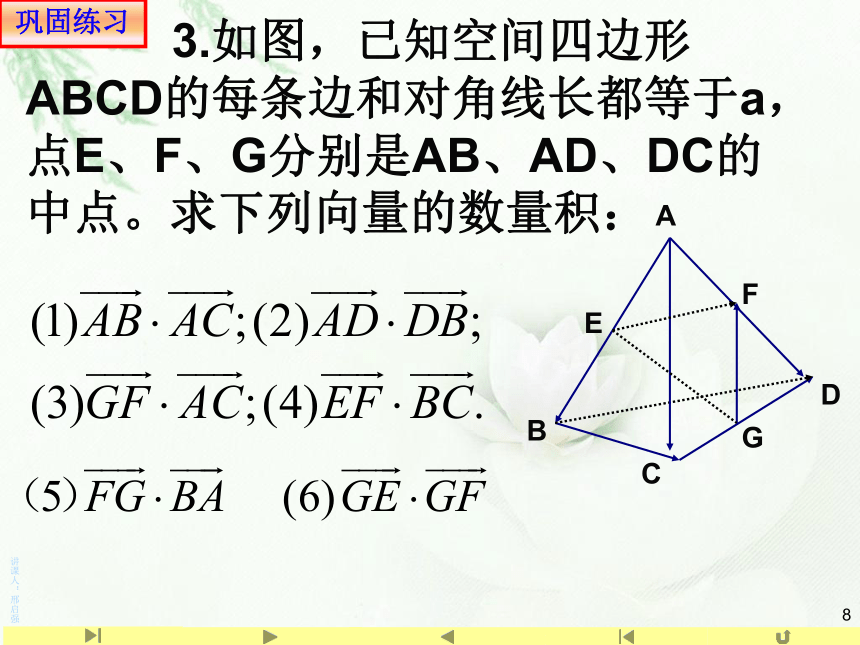
3.如图,已知空间四边形ABCD的每条边和对角线长都等于a,点E、F、G分别是AB、AD、DC的中点。求下列向量的数量积:
A
B
C
D
E
F
G
巩固练习
B
B1
A
A1
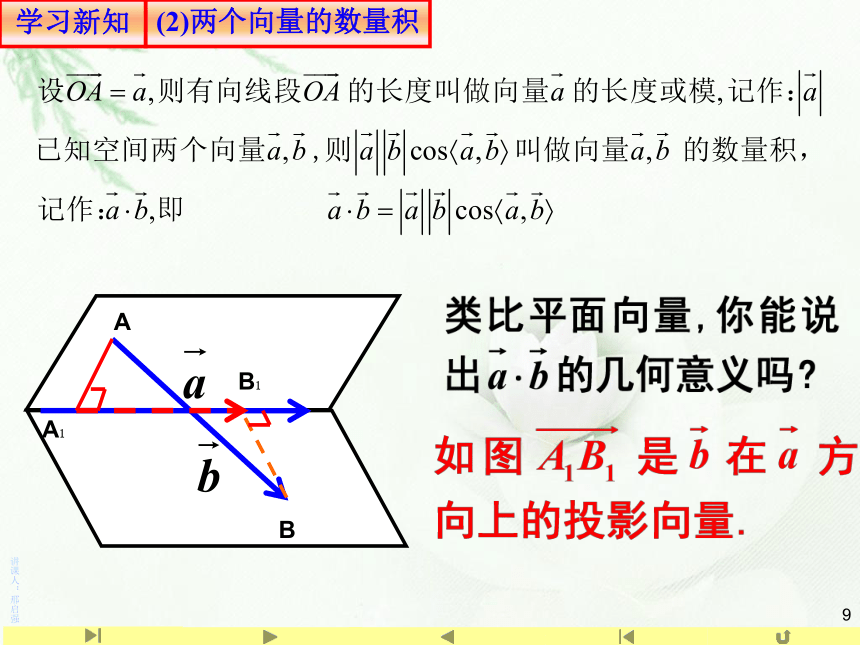
(2)两个向量的数量积
学习新知
思考 :在平面向量的学习中,我们学习了向量的投影。类似地,向量a在向量b上的投影有什么意义?向量a向直线 的投影呢?向量a向平面 的投影呢?
(3)投影向量
学习新知
A1
A1
(3)投影向量
学习新知
例1.已知在平行六面体 中,
,
求对角线 的长。
解:
例题讲评
例2:已知m,n是平面 内的两条相交直线,直线l与 的交点为B,且l⊥m,l⊥n,求证:l⊥
分析:由定义可知,只需证l与平面内任意直线g垂直。
n
m
g
g
m
n
l
l
要证l与g垂直,只需证l·g=0
而m,n不平行,由共面向量定理知,存在唯一的有序实数对(x,y)使得 g=xm+yn
要证l·g=0,只需l· g= xl·m+yl·n=0
故 l·g=0
而l·m=0 ,l·n=0
例题讲评
例2:已知m,n是平面 内的两条相交直线,直线l与 的交点为B,且l⊥m,l⊥n,求证:l⊥
例题讲评
n
m
g
g
m
n
l
l
3.已知在平行六面体 中,
,
求对角线 的长。
解:
习题讲评
4.已知线段 、 在平面 内,
,线段 如果 ,
求 、 之间的距离.
解:∵
习题讲评
l
α
O
P
A
5.已知:如图,PO,PA分别是平面α的垂线,斜线,AO是PA在平面α内的射影,
a
习题讲评
分析:同样可用向量,证明思路几乎一样,只不过其中的加法运算用减法运算来分析.
学习新知
6:已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB
A
B
C
O
习题讲评
例5.如图,已知线段 在平面 内,线段 ,线段 ,线段 ,
,如果 ,求 、 之间的距离。
解:由 ,可知 .
由 知 .
例题讲评
3.已知空间四边形 的每条边和对角线的长都等于 ,点 分别是边 的中点。求证: 。
证明:因为
所以
同理,
巩固练习
巩固练习
巩固练习
5.已知空间向量a,b满足|a|=4,|b|=8,a与b的夹角是150°,
计算:(1)(a+2b)·(2a-b);(2)|4a一2b|.
如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
巩固练习
已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.
巩固练习
1.1.2空间向量的数量积运算
两个向量的夹角的定义
O
A
B
学习新知
两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]
(2)两个向量的数量积
注意: ①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
学习新知
不一定为锐角
不一定为钝角
巩固练习
空间向量的数量积性质
注意:
①性质2)是证明两向量垂直的依据;
②性质3)是求向量的长度(模)的依据;
③性质(5)是用来求两个向量的夹角
对于非零向量 ,有:
学习新知
空间向量的数量积满足的运算律
注意:
数量积不满足结合律即
学习新知
×
×
×
×
巩固练习
3.如图,已知空间四边形ABCD的每条边和对角线长都等于a,点E、F、G分别是AB、AD、DC的中点。求下列向量的数量积:
A
B
C
D
E
F
G
巩固练习
B
B1
A
A1
(2)两个向量的数量积
学习新知
思考 :在平面向量的学习中,我们学习了向量的投影。类似地,向量a在向量b上的投影有什么意义?向量a向直线 的投影呢?向量a向平面 的投影呢?
(3)投影向量
学习新知
A1
A1
(3)投影向量
学习新知
例1.已知在平行六面体 中,
,
求对角线 的长。
解:
例题讲评
例2:已知m,n是平面 内的两条相交直线,直线l与 的交点为B,且l⊥m,l⊥n,求证:l⊥
分析:由定义可知,只需证l与平面内任意直线g垂直。
n
m
g
g
m
n
l
l
要证l与g垂直,只需证l·g=0
而m,n不平行,由共面向量定理知,存在唯一的有序实数对(x,y)使得 g=xm+yn
要证l·g=0,只需l· g= xl·m+yl·n=0
故 l·g=0
而l·m=0 ,l·n=0
例题讲评
例2:已知m,n是平面 内的两条相交直线,直线l与 的交点为B,且l⊥m,l⊥n,求证:l⊥
例题讲评
n
m
g
g
m
n
l
l
3.已知在平行六面体 中,
,
求对角线 的长。
解:
习题讲评
4.已知线段 、 在平面 内,
,线段 如果 ,
求 、 之间的距离.
解:∵
习题讲评
l
α
O
P
A
5.已知:如图,PO,PA分别是平面α的垂线,斜线,AO是PA在平面α内的射影,
a
习题讲评
分析:同样可用向量,证明思路几乎一样,只不过其中的加法运算用减法运算来分析.
学习新知
6:已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB
A
B
C
O
习题讲评
例5.如图,已知线段 在平面 内,线段 ,线段 ,线段 ,
,如果 ,求 、 之间的距离。
解:由 ,可知 .
由 知 .
例题讲评
3.已知空间四边形 的每条边和对角线的长都等于 ,点 分别是边 的中点。求证: 。
证明:因为
所以
同理,
巩固练习
巩固练习
巩固练习
5.已知空间向量a,b满足|a|=4,|b|=8,a与b的夹角是150°,
计算:(1)(a+2b)·(2a-b);(2)|4a一2b|.
如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
巩固练习
已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.
巩固练习
