人教A版(2019)高中数学选择性必修第一册1.2空间向量基本定理习题课(共26张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册1.2空间向量基本定理习题课(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 15:47:34 | ||
图片预览







文档简介
(共26张PPT)
1.2空间向量基本定理
习题课
空间向量基本定理
概念
(1)如果三个向量a,b,c 不共面,那么对空间任一向量p,存在有序实数组(x,y,z),使得p=xa+yb+zc,把{a,b,c}叫做空间的一个基底,a,b,c叫做基向量,空间中任何三个不共面的向量都可以构成空间的一个基底.
(2)基底选定后,空间所有向量均可由基底唯一表示,构成基底的三个向量a,b,c中,没有零向量.
(3)单位正交基底:如果{e1,e2,e3}为单位正交基底,则这三个基向量的位置关系是两两_______,长度为1;且向量e1,e2,e3有公共的_______.
垂直
起点
(2)向量p的坐标是把向量p的起点平移到坐标原点O,则 的终点P的坐标就是向量p的坐标,这样就把空间向量坐标化了.
空间向量的坐标表示
(1)设e1,e2,e3为有公共起点O的三个两两垂直的单位向量(我们称它们为单位正交基底),以e1,e2,e3的公共起点O为原点,分别以e1,e2,e3的方向为x轴、y轴、z轴的正方向建立空间直角坐标系Oxyz,那么对于空间任意一个向量p,一定可以把它平移,使它的起点与原点O重合,得到向量 =p,由空间向量基本定理可知,存在有序实数组(x,y,z),使得p=____________,我们把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记作p=(x,y,z),此时向量p的_____恰是点P在空间直角坐标系Oxyz中的坐标____________.
xe1+ye2+ze3
坐标
(x,y,z)
做一做
典型讲评
例1.如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且
用向量 表示 .
例2.如图,在平行六面体ABCD-A1B1C1D1中,AB=4, AD=4,AA1=5,
∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M, N分别为D1C1,C1B1的中点,求证MN⊥AC1.
典型讲评
典型讲评
例3.如图,正方体ABCD-A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;(2)求CE与AG所成角的余弦值.
所以EF//AC.
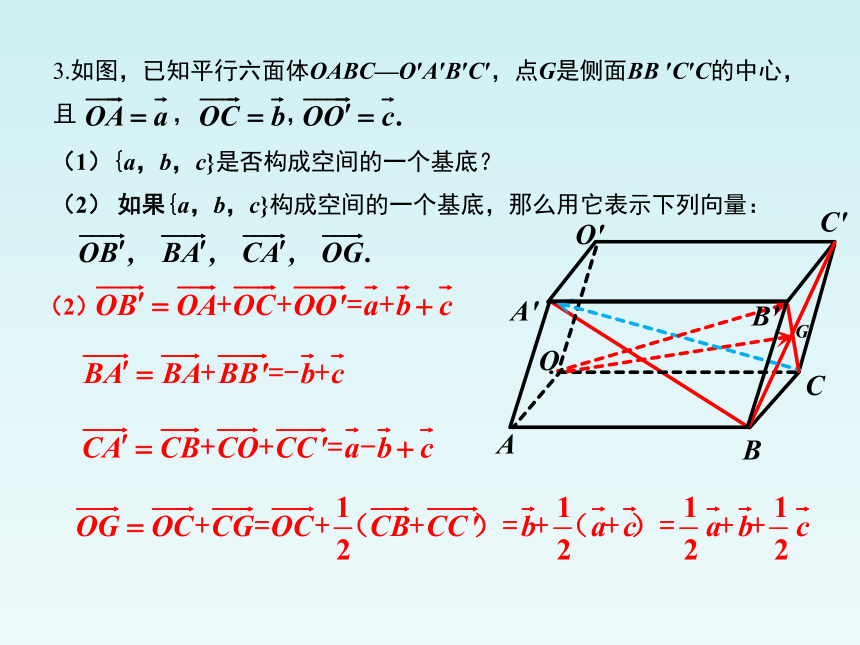
(1){a,b,c}是否构成空间的一个基底?
(2) 如果{a,b,c}构成空间的一个基底,那么用它表示下列向量:
(2)
A
B
C
O
C'
O'
A'
B'
G
3.如图,已知平行六面体OABC—O′A′B′C′,点G是侧面BB ′C′C的中心, 且 , ,
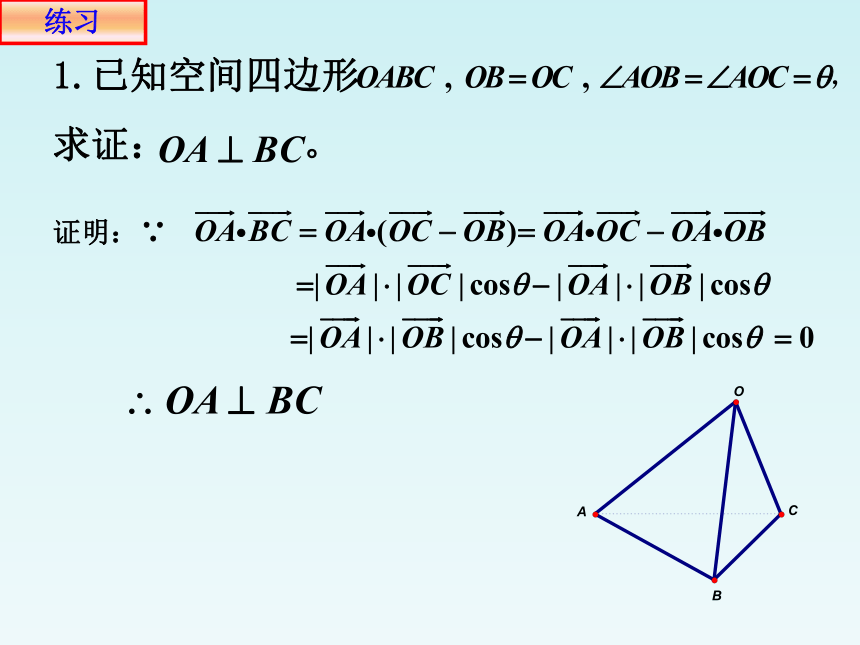
1.已知空间四边形
求证: 。
证明:∵
练习
2.已知在平行六面体 中, ,
求 所成角的余弦值。
解:
D
C
A
B
所以 所成角的余弦值为0。
3.如图,已知在正方体ABCD—A′B′C′D′中,CD′与DC′相交于点O,连接AO,求证:
A
B
C
D
C'
D'
A'
B'
O
解:
∵ABCD—A′B′C′D′是正方体,
4.如图,在空间平移△ABC到△A′B′C′,连结对应顶点.设 ,
,M是BC的中点,N是BC的中点,用基底
表示
5.如图,在长方体ABCD-A1B1C1D1中,M是AC与BD的交点.若D1A1 =2,D1C1 =2 ,D1D=3,求B1M的长.
6.如图,平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60 °, CD=CC1 .
求证:CA1⊥平面C1BD.
D
C
A
B
A1
B1
C1
D1
证明:
∵平行六面体的底面ABCD是菱形,∠C1CB=∠C1CD
=∠BCD=60 °,CD=CC1 .
6.如图,平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60 °, CD=CC1 .
求证:CA1⊥平面C1BD.
D
C
A
B
A1
B1
C1
D1
应用空间向量基本定理证明线线位置关系
7.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG= CD.
(1)证明:EF⊥B1C;
(2)求EF与C1G所成角的余弦值.
F
B
C
D
C1
D1
A1
B1
G
A
E
应用空间向量基本定理证明线线位置关系
7.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG= CD.
(1)证明:EF⊥B1C;
(2)求EF与C1G所成角的余弦值.
F
B
C
D
C1
D1
A1
B1
G
A
E
应用空间向量基本定理证明线线位置关系
7.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG= CD.
(1)证明:EF⊥B1C;
(2)求EF与C1G所成角的余弦值.
F
B
C
D
C1
D1
A1
B1
G
A
E
反思感悟应用空间向量基本定理可以证明空间的线线垂直、线线平行,可求两条异面直线所成的角等.
首先根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0;
(2)若证明线线平行,只需证明两向量共线;
(3)若要求异面直线所成的角,则转化为两向量的夹角(或其补角).
延伸探究设这个正方体中线段A1B的中点为M,证明:MF∥B1C.
1.在正方体ABCD-A1B1C1D1中,可以作为空间向量的一组基底的是( )
C
解析:只有选项C中的三个向量是不共面的,可以作为一个基底.
A
达标练习
3.下列说法正确的是( )
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
C
解析:A项中应是不共面的三个向量构成空间向量的基底;
B项,空间基底有无数个;
D项中因为基底不唯一,所以D错.故选C.
达标练习
达标练习
6、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.
达标练习
应用空间向量基本定理可以证明空间的线线垂直、线线平行,可求两条异面直线所成的角等.
首先根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0;
(2)若证明线线平行,只需证明两向量共线;
(3)若要求异面直线所成的角,则转化为两向量的夹角(或其补角).
课堂小结
5.若{a,b,c}是空间的一个基底,试判断{a+b,b+c,c+a}能否作为空间的一个基底.
解:假设a+b,b+c,c+a共面,则存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),即a+b=μa+λb+(λ+μ)c.
∵{a,b,c}是空间的一个基底,∴a,b,c不共面.
即不存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),
∴a+b,b+c,c+a不共面.
故{a+b,b+c,c+a}能作为空间的一个基底.
1.2空间向量基本定理
习题课
空间向量基本定理
概念
(1)如果三个向量a,b,c 不共面,那么对空间任一向量p,存在有序实数组(x,y,z),使得p=xa+yb+zc,把{a,b,c}叫做空间的一个基底,a,b,c叫做基向量,空间中任何三个不共面的向量都可以构成空间的一个基底.
(2)基底选定后,空间所有向量均可由基底唯一表示,构成基底的三个向量a,b,c中,没有零向量.
(3)单位正交基底:如果{e1,e2,e3}为单位正交基底,则这三个基向量的位置关系是两两_______,长度为1;且向量e1,e2,e3有公共的_______.
垂直
起点
(2)向量p的坐标是把向量p的起点平移到坐标原点O,则 的终点P的坐标就是向量p的坐标,这样就把空间向量坐标化了.
空间向量的坐标表示
(1)设e1,e2,e3为有公共起点O的三个两两垂直的单位向量(我们称它们为单位正交基底),以e1,e2,e3的公共起点O为原点,分别以e1,e2,e3的方向为x轴、y轴、z轴的正方向建立空间直角坐标系Oxyz,那么对于空间任意一个向量p,一定可以把它平移,使它的起点与原点O重合,得到向量 =p,由空间向量基本定理可知,存在有序实数组(x,y,z),使得p=____________,我们把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记作p=(x,y,z),此时向量p的_____恰是点P在空间直角坐标系Oxyz中的坐标____________.
xe1+ye2+ze3
坐标
(x,y,z)
做一做
典型讲评
例1.如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且
用向量 表示 .
例2.如图,在平行六面体ABCD-A1B1C1D1中,AB=4, AD=4,AA1=5,
∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M, N分别为D1C1,C1B1的中点,求证MN⊥AC1.
典型讲评
典型讲评
例3.如图,正方体ABCD-A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;(2)求CE与AG所成角的余弦值.
所以EF//AC.
(1){a,b,c}是否构成空间的一个基底?
(2) 如果{a,b,c}构成空间的一个基底,那么用它表示下列向量:
(2)
A
B
C
O
C'
O'
A'
B'
G
3.如图,已知平行六面体OABC—O′A′B′C′,点G是侧面BB ′C′C的中心, 且 , ,
1.已知空间四边形
求证: 。
证明:∵
练习
2.已知在平行六面体 中, ,
求 所成角的余弦值。
解:
D
C
A
B
所以 所成角的余弦值为0。
3.如图,已知在正方体ABCD—A′B′C′D′中,CD′与DC′相交于点O,连接AO,求证:
A
B
C
D
C'
D'
A'
B'
O
解:
∵ABCD—A′B′C′D′是正方体,
4.如图,在空间平移△ABC到△A′B′C′,连结对应顶点.设 ,
,M是BC的中点,N是BC的中点,用基底
表示
5.如图,在长方体ABCD-A1B1C1D1中,M是AC与BD的交点.若D1A1 =2,D1C1 =2 ,D1D=3,求B1M的长.
6.如图,平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60 °, CD=CC1 .
求证:CA1⊥平面C1BD.
D
C
A
B
A1
B1
C1
D1
证明:
∵平行六面体的底面ABCD是菱形,∠C1CB=∠C1CD
=∠BCD=60 °,CD=CC1 .
6.如图,平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60 °, CD=CC1 .
求证:CA1⊥平面C1BD.
D
C
A
B
A1
B1
C1
D1
应用空间向量基本定理证明线线位置关系
7.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG= CD.
(1)证明:EF⊥B1C;
(2)求EF与C1G所成角的余弦值.
F
B
C
D
C1
D1
A1
B1
G
A
E
应用空间向量基本定理证明线线位置关系
7.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG= CD.
(1)证明:EF⊥B1C;
(2)求EF与C1G所成角的余弦值.
F
B
C
D
C1
D1
A1
B1
G
A
E
应用空间向量基本定理证明线线位置关系
7.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG= CD.
(1)证明:EF⊥B1C;
(2)求EF与C1G所成角的余弦值.
F
B
C
D
C1
D1
A1
B1
G
A
E
反思感悟应用空间向量基本定理可以证明空间的线线垂直、线线平行,可求两条异面直线所成的角等.
首先根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0;
(2)若证明线线平行,只需证明两向量共线;
(3)若要求异面直线所成的角,则转化为两向量的夹角(或其补角).
延伸探究设这个正方体中线段A1B的中点为M,证明:MF∥B1C.
1.在正方体ABCD-A1B1C1D1中,可以作为空间向量的一组基底的是( )
C
解析:只有选项C中的三个向量是不共面的,可以作为一个基底.
A
达标练习
3.下列说法正确的是( )
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
C
解析:A项中应是不共面的三个向量构成空间向量的基底;
B项,空间基底有无数个;
D项中因为基底不唯一,所以D错.故选C.
达标练习
达标练习
6、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.
达标练习
应用空间向量基本定理可以证明空间的线线垂直、线线平行,可求两条异面直线所成的角等.
首先根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0;
(2)若证明线线平行,只需证明两向量共线;
(3)若要求异面直线所成的角,则转化为两向量的夹角(或其补角).
课堂小结
5.若{a,b,c}是空间的一个基底,试判断{a+b,b+c,c+a}能否作为空间的一个基底.
解:假设a+b,b+c,c+a共面,则存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),即a+b=μa+λb+(λ+μ)c.
∵{a,b,c}是空间的一个基底,∴a,b,c不共面.
即不存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),
∴a+b,b+c,c+a不共面.
故{a+b,b+c,c+a}能作为空间的一个基底.
