人教A版(2019)高中数学选择性必修第一册1.3.1空间直角坐标系(共11张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册1.3.1空间直角坐标系(共11张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 15:48:43 | ||
图片预览



文档简介
(共11张PPT)
1.3.1空间直角坐标系
复习引入
共线向量定理:
共面向量定理:
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,
常用{ }表示.
空间向量的基本定理:
若是 空间的一个基底, 是空间任意一向量,存在唯一的实数组使
x
y
z
e1
e2
e3
O
学习新知
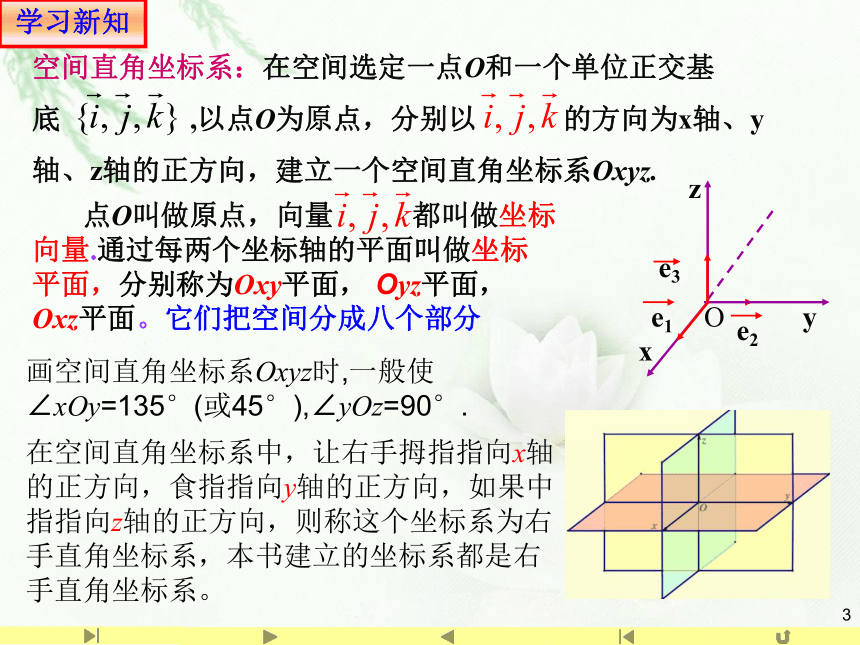
空间直角坐标系:在空间选定一点O和一个单位正交基底 ,以点O为原点,分别以 的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系Oxyz.
点O叫做原点,向量 都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面, Oyz平面, Oxz平面。它们把空间分成八个部分
画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系,本书建立的坐标系都是右手直角坐标系。
x
y
z
O
A(x,y,z)
i
j
k
学习新知
在空间直角坐标系Oxyz中(如图), 为坐标向量,对空间任意一点A,对应一个向量 ,且点A的位置由向量 唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使
在单位正交基底 下与向量 对应的有序实数组 (x,y,z),叫做点A在直角坐标系Oxyz中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点P的纵坐标,z叫做点A的竖坐标.
也就是说,以O为起点的有向线段 (向量)的坐标可以和终点的坐标建立起一一对应的关系,从而互相转化.
x
y
z
O
A(x,y,z)
j
k
i
学习新知
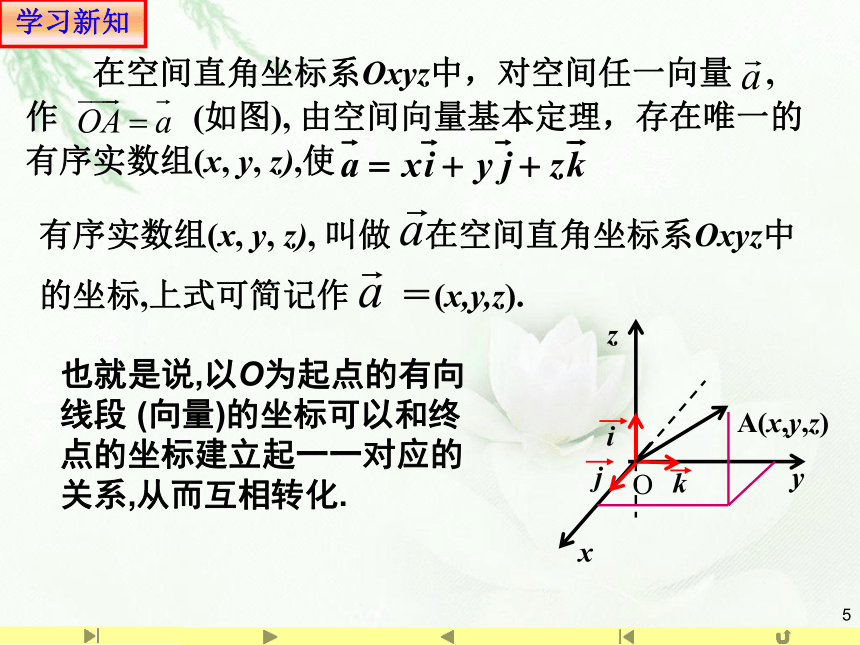
在空间直角坐标系Oxyz中,对空间任一向量 ,
作 (如图), 由空间向量基本定理,存在唯一的有序实数组(x, y, z),使
有序实数组(x, y, z), 叫做 在空间直角坐标系Oxyz中的坐标,上式可简记作 =(x,y,z).
新知探究
在空间直角坐标系Oxyz中,对空间任意一点A,或任意一个向量 ,你能借助几何直观确定它们的坐标(x,y,z)吗?
1、在空间坐标系Oxyz中, ( )分别是与x轴、 y轴、 z轴的正方向相同的单位向量)则 的坐标为 ,点B的坐标为 。
2、点M(2,-3,-4)在坐标平面xOy、xOz、yOz内的正投影的坐标分别为 ,关于原点的对称点为 ,
关于x轴的对称点为 ,
关于y轴的对称点为 ,
关于z轴的对称点为 ,
(2,-3,0)
(2,0,-4)
(0,-3,-4)
(-2, 3,4)
(2, 3, 4)
(-2,-3,4)
(-2,3,-4)
(1,-2,-3)
不确定
巩固练习
求某点P的坐标的方法:
先找到点P在xOy平面上的射影M,过点M向x轴作垂线,确定垂足N.其中|ON|,|NM|,|MP|即为点P坐标的绝对值,再按O→N→M→P确定相应坐标的符号与坐标轴同向为正,反向为负,即可得到相应的点P的坐标.
巩固练习
1.在空间直角坐标系中标出下列各点:
A(0,2,4 ), B(1,0,5),
C(0,2,0), D(1,3,4).
2.在空间直角坐标系Oxyz中,
(1)哪个坐标平面与x轴垂直?哪个坐标平面与y轴垂直?哪个坐标平面与z轴垂直?
(2)写出点P(2,3,4)在三个坐标平面内的射影的坐标.
(3)写出点P(1,3,5)关于原点成中心对称的点的坐标。
巩固练习
1.3.1空间直角坐标系
复习引入
共线向量定理:
共面向量定理:
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,
常用{ }表示.
空间向量的基本定理:
若是 空间的一个基底, 是空间任意一向量,存在唯一的实数组使
x
y
z
e1
e2
e3
O
学习新知
空间直角坐标系:在空间选定一点O和一个单位正交基底 ,以点O为原点,分别以 的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系Oxyz.
点O叫做原点,向量 都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面, Oyz平面, Oxz平面。它们把空间分成八个部分
画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系,本书建立的坐标系都是右手直角坐标系。
x
y
z
O
A(x,y,z)
i
j
k
学习新知
在空间直角坐标系Oxyz中(如图), 为坐标向量,对空间任意一点A,对应一个向量 ,且点A的位置由向量 唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使
在单位正交基底 下与向量 对应的有序实数组 (x,y,z),叫做点A在直角坐标系Oxyz中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点P的纵坐标,z叫做点A的竖坐标.
也就是说,以O为起点的有向线段 (向量)的坐标可以和终点的坐标建立起一一对应的关系,从而互相转化.
x
y
z
O
A(x,y,z)
j
k
i
学习新知
在空间直角坐标系Oxyz中,对空间任一向量 ,
作 (如图), 由空间向量基本定理,存在唯一的有序实数组(x, y, z),使
有序实数组(x, y, z), 叫做 在空间直角坐标系Oxyz中的坐标,上式可简记作 =(x,y,z).
新知探究
在空间直角坐标系Oxyz中,对空间任意一点A,或任意一个向量 ,你能借助几何直观确定它们的坐标(x,y,z)吗?
1、在空间坐标系Oxyz中, ( )分别是与x轴、 y轴、 z轴的正方向相同的单位向量)则 的坐标为 ,点B的坐标为 。
2、点M(2,-3,-4)在坐标平面xOy、xOz、yOz内的正投影的坐标分别为 ,关于原点的对称点为 ,
关于x轴的对称点为 ,
关于y轴的对称点为 ,
关于z轴的对称点为 ,
(2,-3,0)
(2,0,-4)
(0,-3,-4)
(-2, 3,4)
(2, 3, 4)
(-2,-3,4)
(-2,3,-4)
(1,-2,-3)
不确定
巩固练习
求某点P的坐标的方法:
先找到点P在xOy平面上的射影M,过点M向x轴作垂线,确定垂足N.其中|ON|,|NM|,|MP|即为点P坐标的绝对值,再按O→N→M→P确定相应坐标的符号与坐标轴同向为正,反向为负,即可得到相应的点P的坐标.
巩固练习
1.在空间直角坐标系中标出下列各点:
A(0,2,4 ), B(1,0,5),
C(0,2,0), D(1,3,4).
2.在空间直角坐标系Oxyz中,
(1)哪个坐标平面与x轴垂直?哪个坐标平面与y轴垂直?哪个坐标平面与z轴垂直?
(2)写出点P(2,3,4)在三个坐标平面内的射影的坐标.
(3)写出点P(1,3,5)关于原点成中心对称的点的坐标。
巩固练习
