人教A版(2019)高中数学选择性必修第一册1.4.2用空间向量研究距离、夹角问题1(共26张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册1.4.2用空间向量研究距离、夹角问题1(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 16:23:12 | ||
图片预览







文档简介
(共26张PPT)
1.4.2用空间向量研究距离、夹角问题
距离问题
研究
从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.
新课引入
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
问题:空间中包括哪些距离 求解空间距离常用的方法有哪些
答案:点到直线、点到平面、两条平行线及两个平行平面的距离; 传统方法和向量法.
1. 空间两点之间的距离
学习新知
点到直线的距离、两条平行直线之间的距离
2.点到直线的距离
学习新知
2.点到直线的距离
点到直线的距离、两条平行直线之间的距离
3.两条平行直线之间的距离
求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.
典型例题
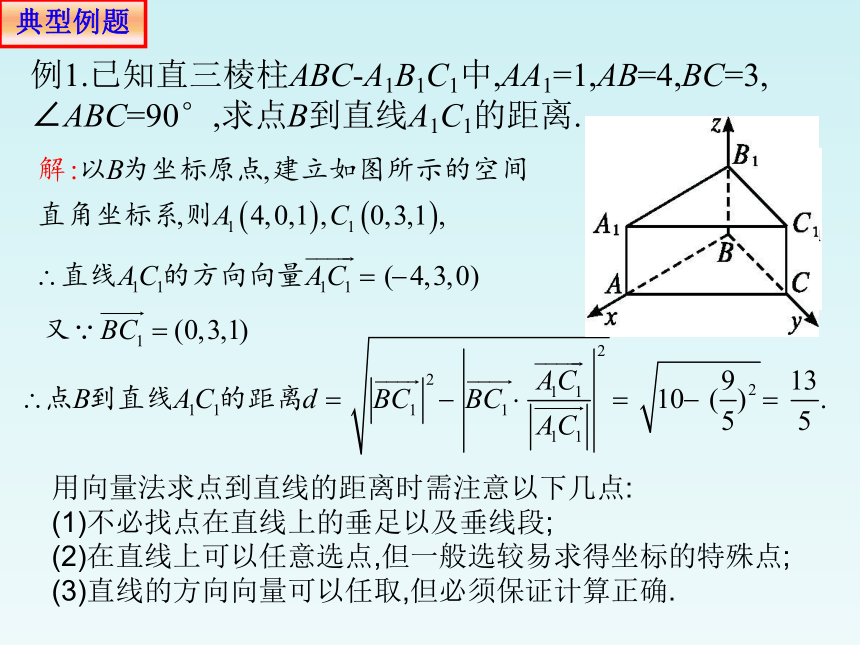
例1.已知直三棱柱ABC-A1B1C1中,AA1=1,AB=4,BC=3,
∠ABC=90°,求点B到直线A1C1的距离.
用向量法求点到直线的距离时需注意以下几点:
(1)不必找点在直线上的垂足以及垂线段;
(2)在直线上可以任意选点,但一般选较易求得坐标的特殊点;
(3)直线的方向向量可以任取,但必须保证计算正确.
1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C,D1A1的中点,则点A到直线EF的距离为 .
巩固练习
向量法求点到平面的距离:
学习新知
点到平面的距离、两个平行平面之间的距离
这个结论说明,平面外一点到平面的距离等于连接此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.
学习新知
点到平面的距离、两个平行平面之间的距离
1.平面外一点到平面的距离等于连结此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.
3.两个平行平面之间的距离
如果两个平面α,β互相平行,在其中一个平面α内任取一点P,可将两个平行平面的距离转化为点P到平面β的距离求解.
2.直线和平面间的距离:
如果一条直线l与一个平面α平行,可在直线l上任取一点P,将线面距离转化为点P到平面α的距离求解.
例2.如图,在棱长为1的正方体ABCD- A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
典型例题
典型例题
典型例题
巩固练习
在正四棱柱ABCD-A1B1C1D1中,底面边长为2,侧棱长为4,则点B1到平面AD1C的距离为 .
解析:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则A(2,0,0),C(0,2,0),D1(0,0,4),B1(2,2,4),
B
C
D
C1
D1
A1
B1
A
典型例题
例3.如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
D
A
B
C
G
F
E
x
y
z
分析:用几何法做相当困难,注意到坐标系建立后各点坐标容易得出,又因为求点到平面的距离可以用法向量来计算,而法向量总是可以快速算出.
例3. 如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
典型例题
D
A
B
C
G
F
E
x
y
z
A
P
D
C
B
M
N
典型例题
A
P
D
C
B
M
N
z
x
y
典型例题
思路分析:
借助平面SAC⊥平面ABC的性质,建立空间直角坐标系,先求平面CMN的法向量,再求距离.
典型例题
解:取AC的中点O,连接OS,OB.∵SA=SC,AB=BC,∴AC⊥SO,AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.又BO 平面ABC,∴SO⊥BO.
如图所示,分别以OA,OB,OS所在直线为x轴,y轴,z轴,建立空间直角坐标系Oxyz,
1.如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1)求点A1到直线B1E的距离;
(2)求直线FC1到直线AE的距离;
(3)求点A1到平面AB1E的距离;
(4)求直线FC1到平面AB1E的距离.
巩固练习
3
解析:以点C为坐标原点,CA,CB,CP所在直线分别为x轴,y轴,
z轴建立如图所示的空间直角坐标系.则A(4,0,0),B(0,3,0),
巩固练习
3.如图,正方体ABCD-A1B1C1D1的棱长为1,O是平面A1B1C1D1的中心,则O到平面ABC1D1的距离是( )
B
4.棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的中点,则直线MN到平面ACD1的距离为 .
解析:如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
巩固练习
5.两平行平面α,β分别经过坐标原点O和点A(2,1,1),且两平面的一个法向量n=(-1,0,1),则两平面间的距离是( )
答案:B
巩固练习
6.若三棱锥P-ABC的三条侧棱两两垂直,且满足PA=PB=PC=1,则点P到平面ABC的距离是( )
答案:D
解析:分别以PA,PB,PC所在的直线为x轴,y轴,z轴建立空间直角坐标系(图略),则A(1,0,0),B(0,1,0),C(0,0,1).可以求得平面ABC的一个
巩固练习
用空间向量解决立体几何问题的“三步曲”。
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义。
(化为向量问题)
(进行向量运算)
(回到图形)
课堂总结
1.4.2用空间向量研究距离、夹角问题
距离问题
研究
从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.
新课引入
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
问题:空间中包括哪些距离 求解空间距离常用的方法有哪些
答案:点到直线、点到平面、两条平行线及两个平行平面的距离; 传统方法和向量法.
1. 空间两点之间的距离
学习新知
点到直线的距离、两条平行直线之间的距离
2.点到直线的距离
学习新知
2.点到直线的距离
点到直线的距离、两条平行直线之间的距离
3.两条平行直线之间的距离
求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.
典型例题
例1.已知直三棱柱ABC-A1B1C1中,AA1=1,AB=4,BC=3,
∠ABC=90°,求点B到直线A1C1的距离.
用向量法求点到直线的距离时需注意以下几点:
(1)不必找点在直线上的垂足以及垂线段;
(2)在直线上可以任意选点,但一般选较易求得坐标的特殊点;
(3)直线的方向向量可以任取,但必须保证计算正确.
1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C,D1A1的中点,则点A到直线EF的距离为 .
巩固练习
向量法求点到平面的距离:
学习新知
点到平面的距离、两个平行平面之间的距离
这个结论说明,平面外一点到平面的距离等于连接此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.
学习新知
点到平面的距离、两个平行平面之间的距离
1.平面外一点到平面的距离等于连结此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.
3.两个平行平面之间的距离
如果两个平面α,β互相平行,在其中一个平面α内任取一点P,可将两个平行平面的距离转化为点P到平面β的距离求解.
2.直线和平面间的距离:
如果一条直线l与一个平面α平行,可在直线l上任取一点P,将线面距离转化为点P到平面α的距离求解.
例2.如图,在棱长为1的正方体ABCD- A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
典型例题
典型例题
典型例题
巩固练习
在正四棱柱ABCD-A1B1C1D1中,底面边长为2,侧棱长为4,则点B1到平面AD1C的距离为 .
解析:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则A(2,0,0),C(0,2,0),D1(0,0,4),B1(2,2,4),
B
C
D
C1
D1
A1
B1
A
典型例题
例3.如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
D
A
B
C
G
F
E
x
y
z
分析:用几何法做相当困难,注意到坐标系建立后各点坐标容易得出,又因为求点到平面的距离可以用法向量来计算,而法向量总是可以快速算出.
例3. 如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
典型例题
D
A
B
C
G
F
E
x
y
z
A
P
D
C
B
M
N
典型例题
A
P
D
C
B
M
N
z
x
y
典型例题
思路分析:
借助平面SAC⊥平面ABC的性质,建立空间直角坐标系,先求平面CMN的法向量,再求距离.
典型例题
解:取AC的中点O,连接OS,OB.∵SA=SC,AB=BC,∴AC⊥SO,AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.又BO 平面ABC,∴SO⊥BO.
如图所示,分别以OA,OB,OS所在直线为x轴,y轴,z轴,建立空间直角坐标系Oxyz,
1.如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1)求点A1到直线B1E的距离;
(2)求直线FC1到直线AE的距离;
(3)求点A1到平面AB1E的距离;
(4)求直线FC1到平面AB1E的距离.
巩固练习
3
解析:以点C为坐标原点,CA,CB,CP所在直线分别为x轴,y轴,
z轴建立如图所示的空间直角坐标系.则A(4,0,0),B(0,3,0),
巩固练习
3.如图,正方体ABCD-A1B1C1D1的棱长为1,O是平面A1B1C1D1的中心,则O到平面ABC1D1的距离是( )
B
4.棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的中点,则直线MN到平面ACD1的距离为 .
解析:如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
巩固练习
5.两平行平面α,β分别经过坐标原点O和点A(2,1,1),且两平面的一个法向量n=(-1,0,1),则两平面间的距离是( )
答案:B
巩固练习
6.若三棱锥P-ABC的三条侧棱两两垂直,且满足PA=PB=PC=1,则点P到平面ABC的距离是( )
答案:D
解析:分别以PA,PB,PC所在的直线为x轴,y轴,z轴建立空间直角坐标系(图略),则A(1,0,0),B(0,1,0),C(0,0,1).可以求得平面ABC的一个
巩固练习
用空间向量解决立体几何问题的“三步曲”。
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义。
(化为向量问题)
(进行向量运算)
(回到图形)
课堂总结
