人教A版(2019)高中数学选择性必修第一册1.4.2用空间向量研究距离、夹角问题2求空间角(共21张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册1.4.2用空间向量研究距离、夹角问题2求空间角(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 963.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 16:24:13 | ||
图片预览





文档简介
(共21张PPT)
求空间角
1.4.2用空间向量研究距离、夹角问题
一、复习引入
用空间向量解决立体几何问题的“三步曲”。
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义。
(化为向量问题)
(进行向量运算)
(回到图形)
复习引入
向量的有关知识:
直线的方向向量:与直线平行的非零向量.
平面的法向量:与平面垂直的向量.
复习引入
典型例题
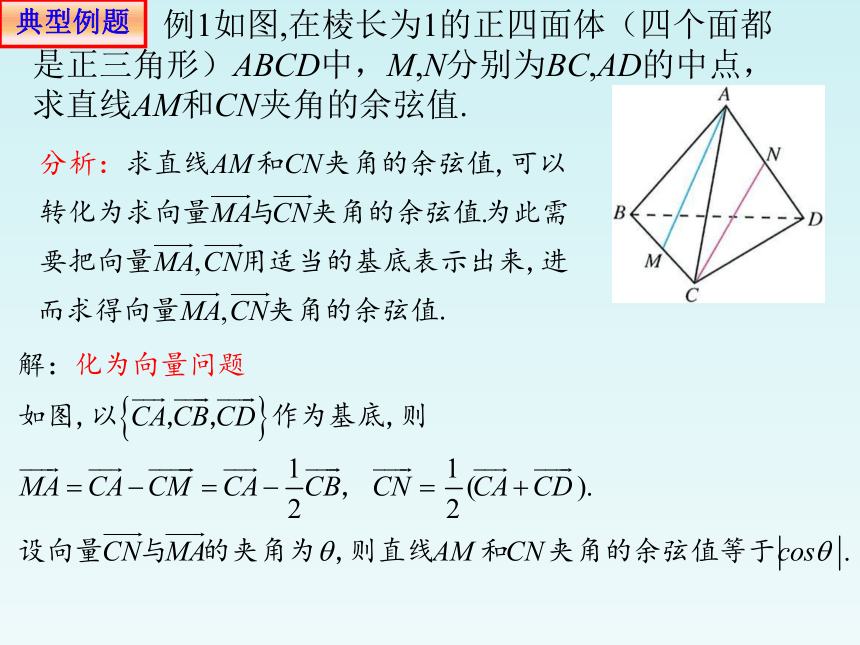
例1如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
典型例题
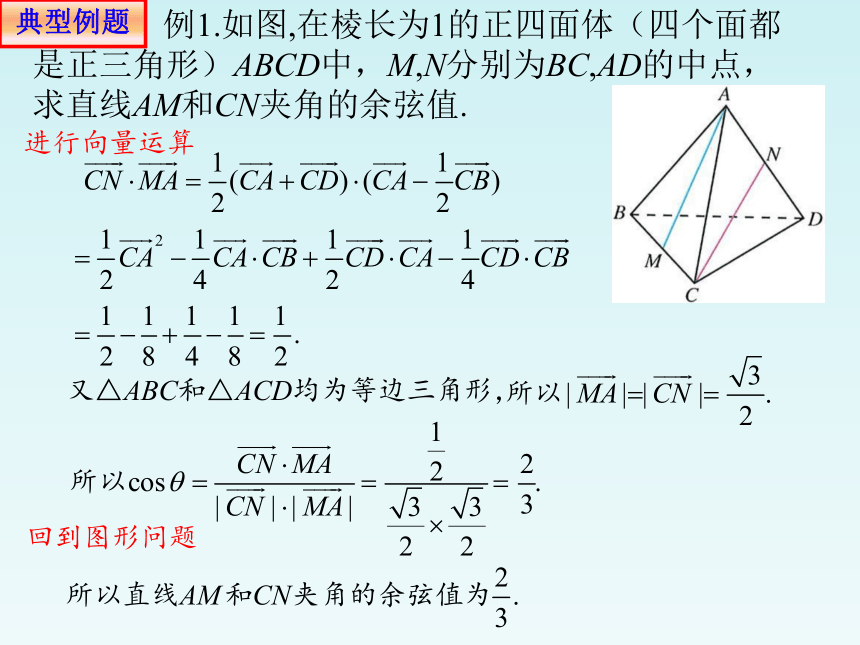
例1.如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
又△ABC和△ACD均为等边三角形,
利用向量方法求两条异面直线所成的角
学习新知
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得。
若异面直线l1,l2所成的角为 ,其方向向量分别为
不要将两异面直线所成的角与其方向向量的夹角等同起来,因为两异面直线所成角的范围是 ,而两个向量夹角的范围是 ,事实上,两异面直线所成的角与其方向向量的夹角是相等或互补的关系.
利用向量方法求直线与平面所成的角
学习新知
利用向量方法求二面角
学习新知
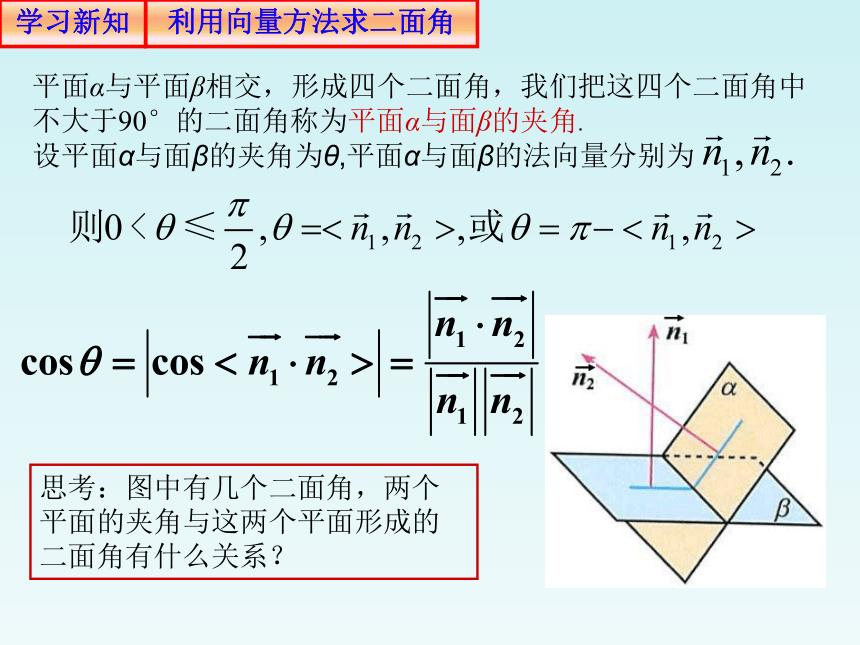
平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与面β的夹角.
设平面α与面β的夹角为θ,平面α与面β的法向量分别为
思考:图中有几个二面角,两个平面的夹角与这两个平面形成的二面角有什么关系?
典型例题
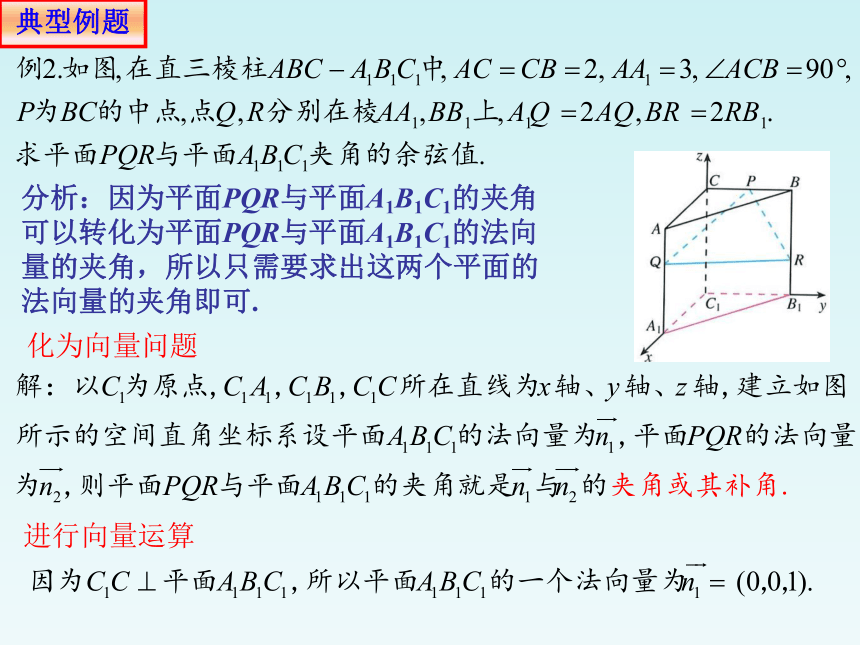
分析:因为平面PQR与平面A1B1C1的夹角可以转化为平面PQR与平面A1B1C1的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
化为向量问题
进行向量运算
回到图形问题
巩固练习
1.如图所示,在三棱柱ABC-A1B1C1中, ∠ABC=90°,AA1⊥底面ABC,AB=BC=AA1, 点E,F分别是棱AB,BB1的中点,试求直线EF和BC1所成的角.
1.利用空间向量求两异面直线所成角的步骤.
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点.
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是 ,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
方法感悟
解:如图建立坐标系A-xyz,则
N
B
A
D
C
B1
C1
D1
A1
M
巩固练习
巩固练习
N
B
A
D
C
B1
C1
D1
A1
M
若直线l与平面α的夹角为θ,利用法向量计算θ的步骤如下:
方法感悟
3.如图,在正方体ABEF-DCE'F'中,M,N分别为AC,BF的中点,求平面MNA与平面MNB的夹角的余弦值.
解:设正方体棱长为1.以B为坐标原点,BA,BE,BC所在直线分别为x轴,y轴,z轴建立空间直角坐标系B-xyz,则
巩固练习
利用向量方法求两平面夹角大小时,多采用法向量法.即求出两个面的法向量,然后通过法向量的夹角来得到两平面夹角.需注意法向量夹角范围是[0,π],而两平面夹角范围是
方法感悟
D
B
A
C
E
P
x
z
y
巩固练习
4.如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,PA=AB=1,AD= ,在线段BC上是否存在一点E,使PA与平面PDE所成角的大小为45o 若存在,确定点E的位置;
若不存在说明理由。
5.如图,在四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC, AB=AD=PB=3. 点E在棱PA上,且PE=2EA.求平面ABE与平面DBE夹角的余弦值.
巩固练习
求空间角
1.4.2用空间向量研究距离、夹角问题
一、复习引入
用空间向量解决立体几何问题的“三步曲”。
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义。
(化为向量问题)
(进行向量运算)
(回到图形)
复习引入
向量的有关知识:
直线的方向向量:与直线平行的非零向量.
平面的法向量:与平面垂直的向量.
复习引入
典型例题
例1如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
典型例题
例1.如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
又△ABC和△ACD均为等边三角形,
利用向量方法求两条异面直线所成的角
学习新知
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得。
若异面直线l1,l2所成的角为 ,其方向向量分别为
不要将两异面直线所成的角与其方向向量的夹角等同起来,因为两异面直线所成角的范围是 ,而两个向量夹角的范围是 ,事实上,两异面直线所成的角与其方向向量的夹角是相等或互补的关系.
利用向量方法求直线与平面所成的角
学习新知
利用向量方法求二面角
学习新知
平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与面β的夹角.
设平面α与面β的夹角为θ,平面α与面β的法向量分别为
思考:图中有几个二面角,两个平面的夹角与这两个平面形成的二面角有什么关系?
典型例题
分析:因为平面PQR与平面A1B1C1的夹角可以转化为平面PQR与平面A1B1C1的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
化为向量问题
进行向量运算
回到图形问题
巩固练习
1.如图所示,在三棱柱ABC-A1B1C1中, ∠ABC=90°,AA1⊥底面ABC,AB=BC=AA1, 点E,F分别是棱AB,BB1的中点,试求直线EF和BC1所成的角.
1.利用空间向量求两异面直线所成角的步骤.
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点.
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是 ,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
方法感悟
解:如图建立坐标系A-xyz,则
N
B
A
D
C
B1
C1
D1
A1
M
巩固练习
巩固练习
N
B
A
D
C
B1
C1
D1
A1
M
若直线l与平面α的夹角为θ,利用法向量计算θ的步骤如下:
方法感悟
3.如图,在正方体ABEF-DCE'F'中,M,N分别为AC,BF的中点,求平面MNA与平面MNB的夹角的余弦值.
解:设正方体棱长为1.以B为坐标原点,BA,BE,BC所在直线分别为x轴,y轴,z轴建立空间直角坐标系B-xyz,则
巩固练习
利用向量方法求两平面夹角大小时,多采用法向量法.即求出两个面的法向量,然后通过法向量的夹角来得到两平面夹角.需注意法向量夹角范围是[0,π],而两平面夹角范围是
方法感悟
D
B
A
C
E
P
x
z
y
巩固练习
4.如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,PA=AB=1,AD= ,在线段BC上是否存在一点E,使PA与平面PDE所成角的大小为45o 若存在,确定点E的位置;
若不存在说明理由。
5.如图,在四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC, AB=AD=PB=3. 点E在棱PA上,且PE=2EA.求平面ABE与平面DBE夹角的余弦值.
巩固练习
