沪科版数学八年级下册第19章第1节《勾股定理》
文档属性
| 名称 | 沪科版数学八年级下册第19章第1节《勾股定理》 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-10 18:06:19 | ||
图片预览




文档简介
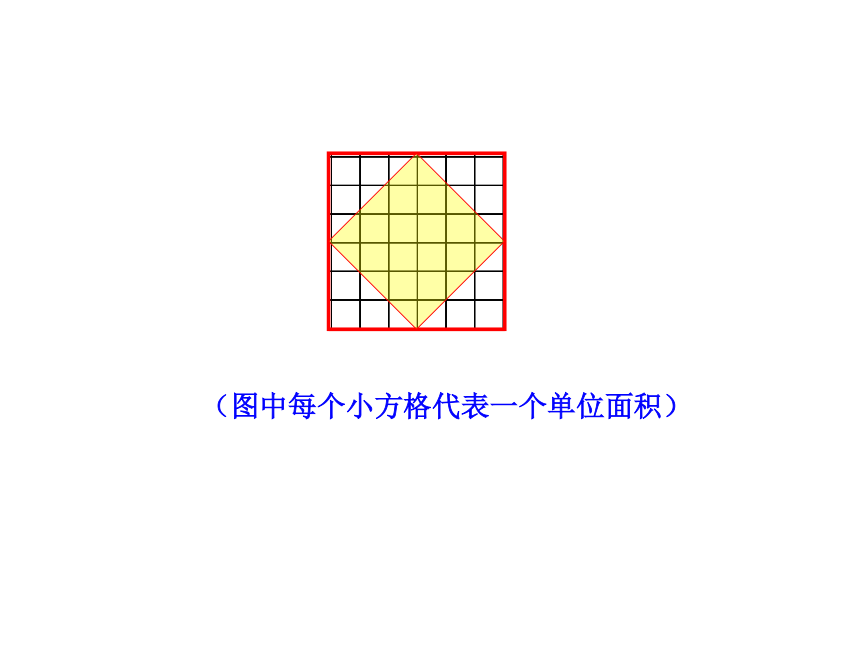
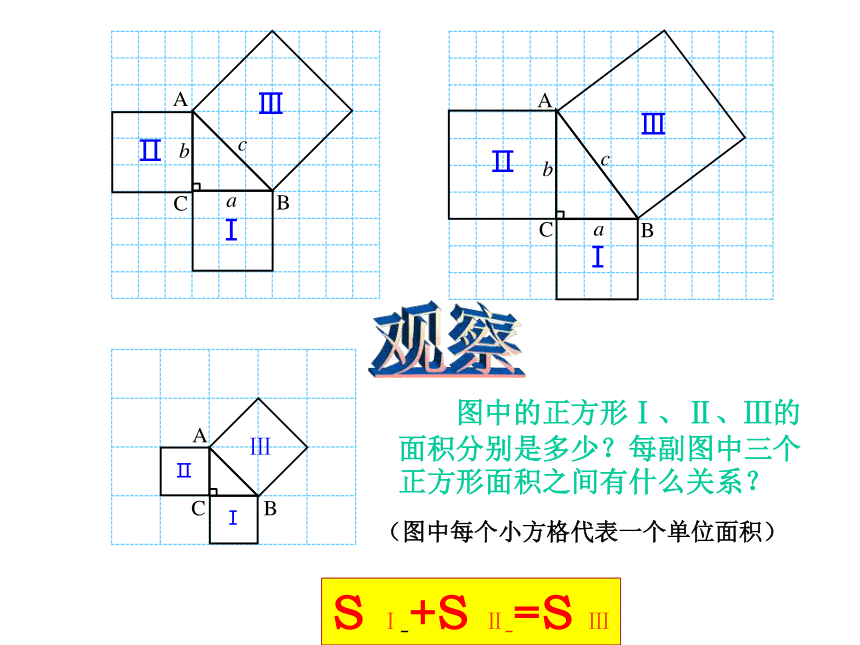
课件22张PPT。19.1勾股定理八年级数学(下册)? 沪科版(图中每个小方格代表一个单位面积) 图中的正方形Ⅰ、Ⅱ、Ⅲ的面积分别是多少?每副图中三个正方形面积之间有什么关系?观察(图中每个小方格代表一个单位面积)S Ⅰ +S Ⅱ =S Ⅲ学生编号正方形面 积S1+S2=S3
S1+S2=S3
S1+S2=S3
S1+S2=S3
S1+S2=S3
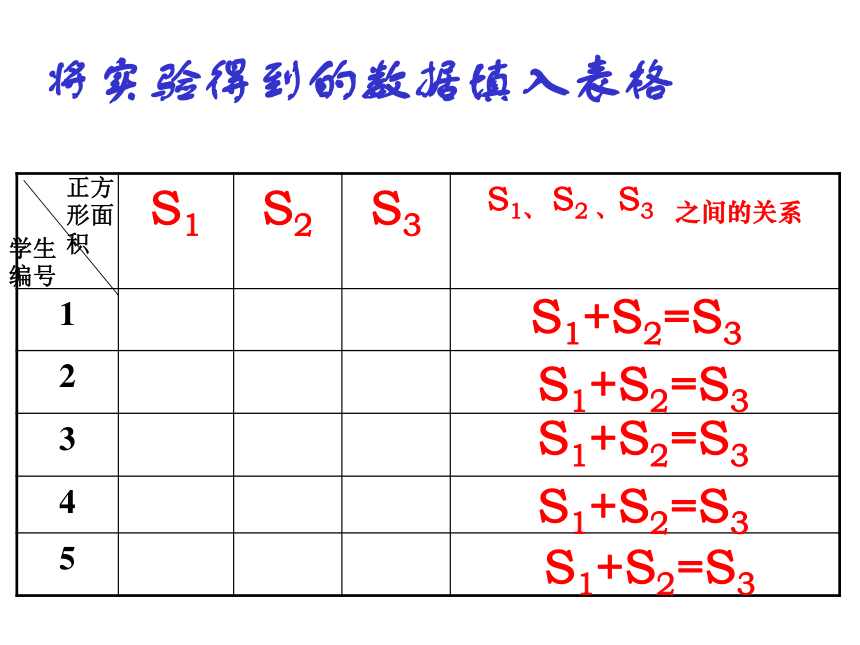
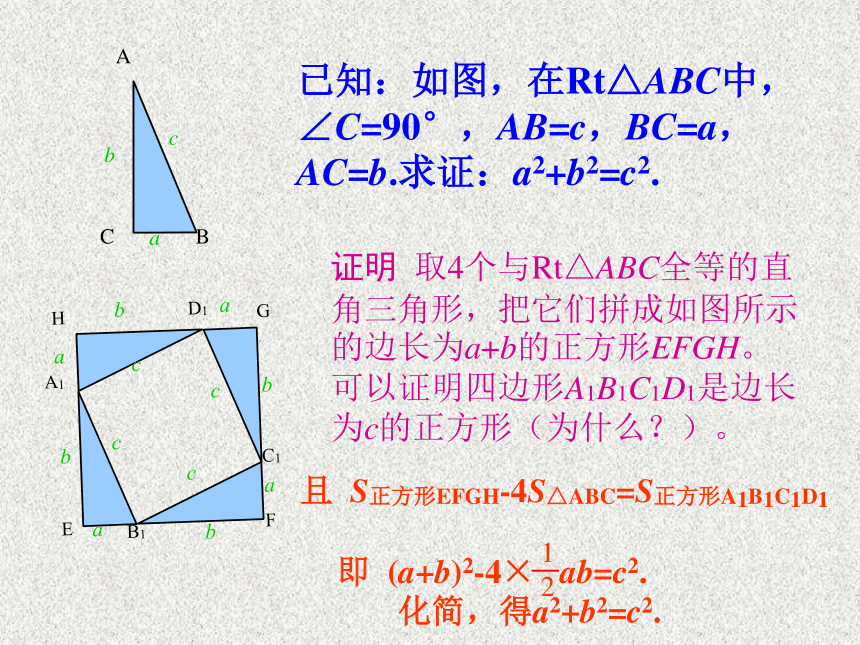
将实验得到的数据填入表格结论: a2+b2=c2即: 两直边的平方和等于斜边的平方已知:如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.求证:a2+b2=c2.证明 取4个与Rt△ABC全等的直角三角形,把它们拼成如图所示的边长为a+b的正方形EFGH。
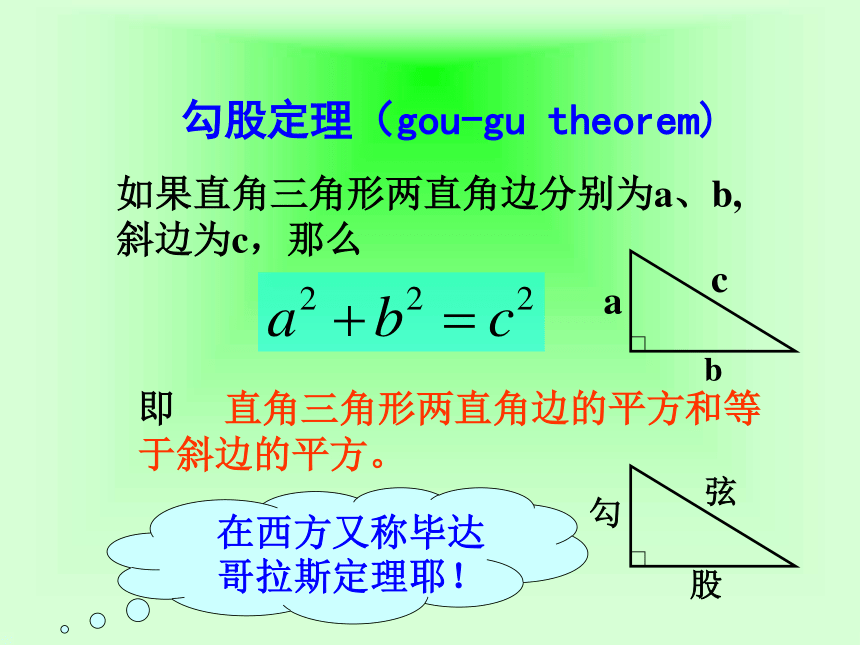
可以证明四边形A1B1C1D1是边长为c的正方形(为什么?)。且 S正方形EFGH-4S△ABC=S正方形A1B1C1D1即 (a+b)2-4× ab=c2.化简,得a2+b2=c2. 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③小试牛刀X=15Y=5Z=7比一比看看谁算得快!2.求下列直角三角形中未知边的长:8x171620x125x小试牛刀X=15X=12X=13①②③1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C34CBA2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=13千米,CB=12千米,则AB为 ( )A.5千米 B.12千米 C.10千米 D.13千米13 12 ?A25 3、已知:Rt△ABC中,AB=4,AC=3,则BC2的长为 . 或74、如图,受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高? 在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2盛开的水莲应用知识回归生活 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。邮票赏析这是1955年希腊曾经发行的纪念一位数学家的邮票。观察这枚邮票图案小方格的个数,你有什么发现?1这节课你学到了什么知识?小 结:3、你还有什么疑惑或没有弄懂的地方?2 运用“勾股定理”应注意什么问题?作业P53 练习 第1、2、3题敬请指导再见
S1+S2=S3
S1+S2=S3
S1+S2=S3
S1+S2=S3
将实验得到的数据填入表格结论: a2+b2=c2即: 两直边的平方和等于斜边的平方已知:如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.求证:a2+b2=c2.证明 取4个与Rt△ABC全等的直角三角形,把它们拼成如图所示的边长为a+b的正方形EFGH。
可以证明四边形A1B1C1D1是边长为c的正方形(为什么?)。且 S正方形EFGH-4S△ABC=S正方形A1B1C1D1即 (a+b)2-4× ab=c2.化简,得a2+b2=c2. 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③小试牛刀X=15Y=5Z=7比一比看看谁算得快!2.求下列直角三角形中未知边的长:8x171620x125x小试牛刀X=15X=12X=13①②③1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C34CBA2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=13千米,CB=12千米,则AB为 ( )A.5千米 B.12千米 C.10千米 D.13千米13 12 ?A25 3、已知:Rt△ABC中,AB=4,AC=3,则BC2的长为 . 或74、如图,受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高? 在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2盛开的水莲应用知识回归生活 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。邮票赏析这是1955年希腊曾经发行的纪念一位数学家的邮票。观察这枚邮票图案小方格的个数,你有什么发现?1这节课你学到了什么知识?小 结:3、你还有什么疑惑或没有弄懂的地方?2 运用“勾股定理”应注意什么问题?作业P53 练习 第1、2、3题敬请指导再见
