10.1.4概率的基本性质 课件(共23张PPT)
文档属性
| 名称 | 10.1.4概率的基本性质 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 17:35:27 | ||
图片预览








文档简介
(共23张PPT)
2022
第十章概率
10.1.4概率的基本性质
目录
CONTENTS
01
知识回顾
03
典型例题
02
概率的性质
04
课堂总结
01
知识回顾
1.古典概型?
具有以上两个特征:
1.有限性:样本空间的样本点只有有限个;
2.等可能性:每个样本点发生的可能性相等。
我们将该试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。
2.古典概型的概率公式?
3.事件的关系和运算?
事件的关系或运算 含义 符合表示
包含 A发生导致B发生 A B或B A
并事件(和事件) A与B至少一个发生 A∪B或A+B
交事件(积事件) A与B同时发生 A∩B或AB
互斥(互不相容) A与B不能同时发生 A∩B=
互为对立 A与B有且只有一个发生 A∩B= ,A∪B=Ω
思考
一般而言,给出了一个数学对象的定义,就可以从定义出发研究这个数学对象的性质.
例如:在给出指数函数的定义后,我们通过定义域、值域、单调性、特殊点等角度来研究函数性质.
类似地,在给出了概率的定义后,你认为可以从哪些角度研究概率的性质
① 概率的取值范围;
② 特殊事件的概率;
③ 事件有某些特殊关系时,它们的概率之间的关系.
02
概率的性质
概率的性质
一般地,概率有如下性质:
性质1:对任意的事件A,都有P(A)≥0.
性质2:必然事件的概率为1, 即P(Ω)=1;
不可能事件的概率为0, 即P( )=0.
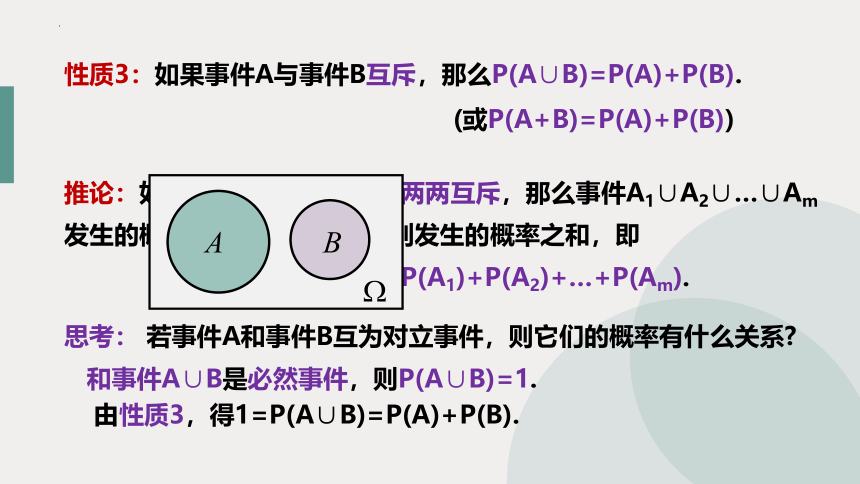
性质3:如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
(或P(A+B)=P(A)+P(B))
推论:如果事件A1, A2, …, Am两两互斥,那么事件A1∪A2∪…∪Am发生的概率等于这m个事件分别发生的概率之和,即
P(A1∪A2∪…∪Am)=P(A1)+P(A2)+…+P(Am).
思考: 若事件A和事件B互为对立事件,则它们的概率有什么关系
和事件A∪B是必然事件,则P(A∪B)=1.
由性质3,得1=P(A∪B)=P(A)+P(B).
性质4: 如果事件A与事件B互为对立事件,那么P(A)+P(B)=1;
即P(B)=1-P(A);
即P(A)=1-P(B).
性质5:(概率的单调性) 如果A B,那么P(A)≤P(B).
所以对于任意事件A,有0≤P(A)≤1.
因为 A Ω,所以P( )≤P(A)≤P(Ω),
思考: 若事件A和事件B只是一个试验中的事件,则它们的概率有什么关系
性质6 :设A、B是一个随机试验中的两个事件,则有
P(A∪B)=P(A)+P(B)-P(A∩B).
或P(A+B)=P(A)+P(B)-P(AB).
思考: 如果是两个以上事件呢,则它们的概率有什么关系
推论:设A、B、C是一个随机试验中的三个事件,则有P(A∪B∪C)=P(A)+P(B)+P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C).
或P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC).
03
典型例题
例1:判断正误(1)任一事件的概率总在(0,1)内.( )(2)不可能事件的概率不一定为0 .( )(3)某地区明天下雨的概率为0.4,明天不下雨的概率为0.5 .( )(4)如果事件A与事件B互斥,那么P(A)+P(B)≤1.( )
×
×
×
√
例2:已知P(A)=0.5,P(B)=0.3.
(1) 如果B A,那么P(A∪B)=_____ ,P(AB)=______ ;
(2) 如果A, B互斥,那么P(A∪B)=_____ ,P(AB)=_____.
0.5
0.3
0.8
0
例3:从一批羽毛球中任取一个,如果其质量小于4.8 g的概率是0.3,质量不小于4.85 g的概率是0.32,那么质量在[4.8,4.85)内的概率是( )A.0.62 B.0.38C.0.70 D.0.68
例4:投掷一枚质地均匀的骰子,向上的一面出现1点,2点,3点,4点,5点,6点的概率相等,记事件A为“出现奇数点”,事件B“向上的点数不超过3”,则P(A∪B)=________.
例5:一名射击运动员在一次射击中射中10环,9环,8环,7环,7环以下概率分别为0.24,0.28,0.19,0.16,0.13.该射击运动员在一次射击中:(1) 射中10环或9环的概率;(2) 至少射中7环的概率.
解析:设“10环,9环,8环,7环,7环以下”的事件分别为A,B,C,D,E. 它们彼此之间互斥,P(A)=0.24,P(B)=0.28,P(C)=0.19,P(D)=0.16,P(E)=0.13.
(1)设“射中10环或9环”为事件M,则有M=A∪B,
∴P(M)=P(A∪B)=P(A)+P(B)=0.24+0.28=0.52,
所以射中10环或9环的概率为0.52.
(2)设“至少射中7环”为事件N,事件N与事件E“是对立事件,
∴ P(N)=1-P(E)=1-0.13=0.87.
所以至少射中7环的概率为0.87.
例6:某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示.现从中随机抽取一名队员,求:(1)该队员只属于一支球队的概率;(2)该队员最多属于两支球队的概率.
例6:某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示.现从中随机抽取一名队员,求:(1)该队员只属于一支球队的概率;(2)该队员最多属于两支球队的概率.
例7:某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为不合格.假设此人对A和B两种饮料没有鉴别能力.(1)求此人被评为优秀的概率;(2)求此人被评为良好及以上的概率.
例8:在学校运动会开幕式上,100 名学生组成一个方阵进行表演,他们按照性别(M (男)、F (女) )及年级(G1 (高一)、G2(高二)、G3(高三))分类统计的人数如下表:
若从这100名学生中随机选一名学生, 求下列概率:
P(M) =______,P(F) =______,
P(M∪F) =______, P(MF) =______,
P(G1) = ______, P(M∪G2) =_______, P(FG3) =______.
G1 G2 G3
M 18 20 14
F 17 24 7
0.52
0.48
1
0
0.35
0.76
0.07
04
课堂总结
课堂总结
概率公式的基本性质:
性质1 对任意的事件A,都有P(A)≥0.
性质2 必然事件的概率为1,不可能事件的概率为0,即
P(Ω)=1,P( )=0.
性质3 如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
性质4 如果事件A与事件B互为对立事件,那么
P(B)=1-P(A),P(A)=1-P(B). 即P(A)+P(B)=1.
性质5 如果A B,那么P(A)≤P(B).
性质6 设A、B是一个随机试验中的两个事件,则有
P(A∪B)=P(A)+P(B)-P(A∩B).(或P(A+B)=P(A)+P(B)-P(AB).)
对任意事件A,有P(A)∈[0,1].
THANKS
感谢观看
2022
第十章概率
10.1.4概率的基本性质
目录
CONTENTS
01
知识回顾
03
典型例题
02
概率的性质
04
课堂总结
01
知识回顾
1.古典概型?
具有以上两个特征:
1.有限性:样本空间的样本点只有有限个;
2.等可能性:每个样本点发生的可能性相等。
我们将该试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。
2.古典概型的概率公式?
3.事件的关系和运算?
事件的关系或运算 含义 符合表示
包含 A发生导致B发生 A B或B A
并事件(和事件) A与B至少一个发生 A∪B或A+B
交事件(积事件) A与B同时发生 A∩B或AB
互斥(互不相容) A与B不能同时发生 A∩B=
互为对立 A与B有且只有一个发生 A∩B= ,A∪B=Ω
思考
一般而言,给出了一个数学对象的定义,就可以从定义出发研究这个数学对象的性质.
例如:在给出指数函数的定义后,我们通过定义域、值域、单调性、特殊点等角度来研究函数性质.
类似地,在给出了概率的定义后,你认为可以从哪些角度研究概率的性质
① 概率的取值范围;
② 特殊事件的概率;
③ 事件有某些特殊关系时,它们的概率之间的关系.
02
概率的性质
概率的性质
一般地,概率有如下性质:
性质1:对任意的事件A,都有P(A)≥0.
性质2:必然事件的概率为1, 即P(Ω)=1;
不可能事件的概率为0, 即P( )=0.
性质3:如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
(或P(A+B)=P(A)+P(B))
推论:如果事件A1, A2, …, Am两两互斥,那么事件A1∪A2∪…∪Am发生的概率等于这m个事件分别发生的概率之和,即
P(A1∪A2∪…∪Am)=P(A1)+P(A2)+…+P(Am).
思考: 若事件A和事件B互为对立事件,则它们的概率有什么关系
和事件A∪B是必然事件,则P(A∪B)=1.
由性质3,得1=P(A∪B)=P(A)+P(B).
性质4: 如果事件A与事件B互为对立事件,那么P(A)+P(B)=1;
即P(B)=1-P(A);
即P(A)=1-P(B).
性质5:(概率的单调性) 如果A B,那么P(A)≤P(B).
所以对于任意事件A,有0≤P(A)≤1.
因为 A Ω,所以P( )≤P(A)≤P(Ω),
思考: 若事件A和事件B只是一个试验中的事件,则它们的概率有什么关系
性质6 :设A、B是一个随机试验中的两个事件,则有
P(A∪B)=P(A)+P(B)-P(A∩B).
或P(A+B)=P(A)+P(B)-P(AB).
思考: 如果是两个以上事件呢,则它们的概率有什么关系
推论:设A、B、C是一个随机试验中的三个事件,则有P(A∪B∪C)=P(A)+P(B)+P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C).
或P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC).
03
典型例题
例1:判断正误(1)任一事件的概率总在(0,1)内.( )(2)不可能事件的概率不一定为0 .( )(3)某地区明天下雨的概率为0.4,明天不下雨的概率为0.5 .( )(4)如果事件A与事件B互斥,那么P(A)+P(B)≤1.( )
×
×
×
√
例2:已知P(A)=0.5,P(B)=0.3.
(1) 如果B A,那么P(A∪B)=_____ ,P(AB)=______ ;
(2) 如果A, B互斥,那么P(A∪B)=_____ ,P(AB)=_____.
0.5
0.3
0.8
0
例3:从一批羽毛球中任取一个,如果其质量小于4.8 g的概率是0.3,质量不小于4.85 g的概率是0.32,那么质量在[4.8,4.85)内的概率是( )A.0.62 B.0.38C.0.70 D.0.68
例4:投掷一枚质地均匀的骰子,向上的一面出现1点,2点,3点,4点,5点,6点的概率相等,记事件A为“出现奇数点”,事件B“向上的点数不超过3”,则P(A∪B)=________.
例5:一名射击运动员在一次射击中射中10环,9环,8环,7环,7环以下概率分别为0.24,0.28,0.19,0.16,0.13.该射击运动员在一次射击中:(1) 射中10环或9环的概率;(2) 至少射中7环的概率.
解析:设“10环,9环,8环,7环,7环以下”的事件分别为A,B,C,D,E. 它们彼此之间互斥,P(A)=0.24,P(B)=0.28,P(C)=0.19,P(D)=0.16,P(E)=0.13.
(1)设“射中10环或9环”为事件M,则有M=A∪B,
∴P(M)=P(A∪B)=P(A)+P(B)=0.24+0.28=0.52,
所以射中10环或9环的概率为0.52.
(2)设“至少射中7环”为事件N,事件N与事件E“是对立事件,
∴ P(N)=1-P(E)=1-0.13=0.87.
所以至少射中7环的概率为0.87.
例6:某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示.现从中随机抽取一名队员,求:(1)该队员只属于一支球队的概率;(2)该队员最多属于两支球队的概率.
例6:某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示.现从中随机抽取一名队员,求:(1)该队员只属于一支球队的概率;(2)该队员最多属于两支球队的概率.
例7:某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为不合格.假设此人对A和B两种饮料没有鉴别能力.(1)求此人被评为优秀的概率;(2)求此人被评为良好及以上的概率.
例8:在学校运动会开幕式上,100 名学生组成一个方阵进行表演,他们按照性别(M (男)、F (女) )及年级(G1 (高一)、G2(高二)、G3(高三))分类统计的人数如下表:
若从这100名学生中随机选一名学生, 求下列概率:
P(M) =______,P(F) =______,
P(M∪F) =______, P(MF) =______,
P(G1) = ______, P(M∪G2) =_______, P(FG3) =______.
G1 G2 G3
M 18 20 14
F 17 24 7
0.52
0.48
1
0
0.35
0.76
0.07
04
课堂总结
课堂总结
概率公式的基本性质:
性质1 对任意的事件A,都有P(A)≥0.
性质2 必然事件的概率为1,不可能事件的概率为0,即
P(Ω)=1,P( )=0.
性质3 如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
性质4 如果事件A与事件B互为对立事件,那么
P(B)=1-P(A),P(A)=1-P(B). 即P(A)+P(B)=1.
性质5 如果A B,那么P(A)≤P(B).
性质6 设A、B是一个随机试验中的两个事件,则有
P(A∪B)=P(A)+P(B)-P(A∩B).(或P(A+B)=P(A)+P(B)-P(AB).)
对任意事件A,有P(A)∈[0,1].
THANKS
感谢观看
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
