5.1.3 同位角 内错角 同旁内角
文档属性
| 名称 | 5.1.3 同位角 内错角 同旁内角 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-10 22:55:11 | ||
图片预览





文档简介
课件29张PPT。复习提问:
1、垂线的定义。
2、垂线有什的性质?
3、什么叫点到直线的距离?垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.5.1.3同位角
内错角
同旁内角(1)了解同位角、内错角、同旁内角的概念.
(2)通过在图形中识别同位角、内错角、同旁内角,提高识图能力,体会分类的思想.
学习重点:
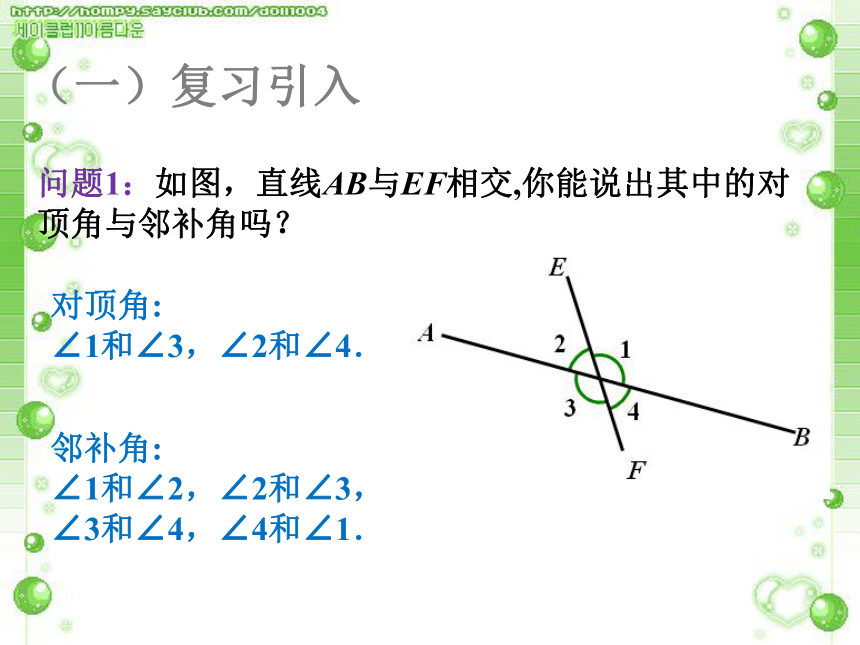
同位角、内错角、同旁内角的识别.学习目标:问题1:如图,直线AB与EF相交,你能说出其中的对顶角与邻补角吗?(一)复习引入对顶角:
∠1和∠3,∠2和∠4.邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.(二)探索与思考问题2:
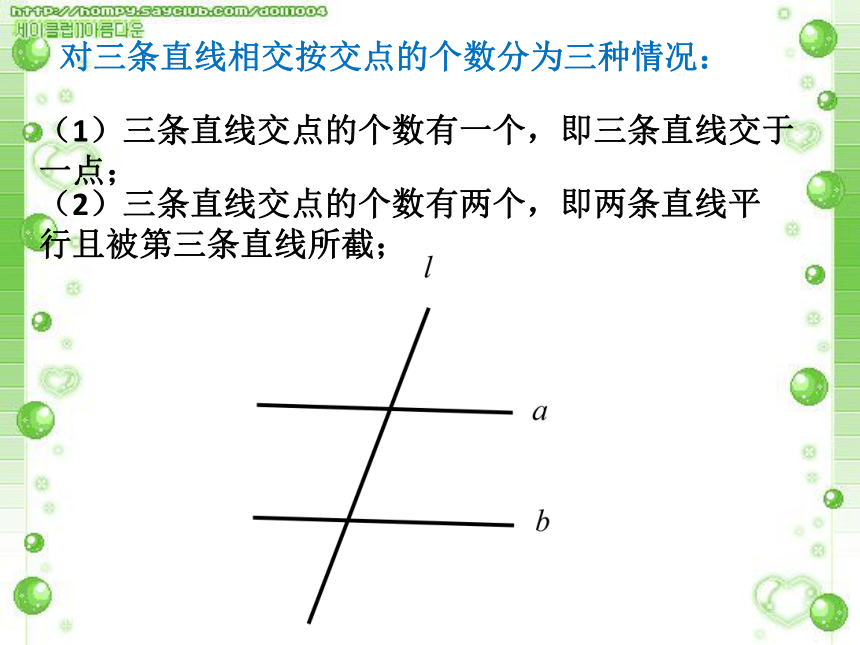
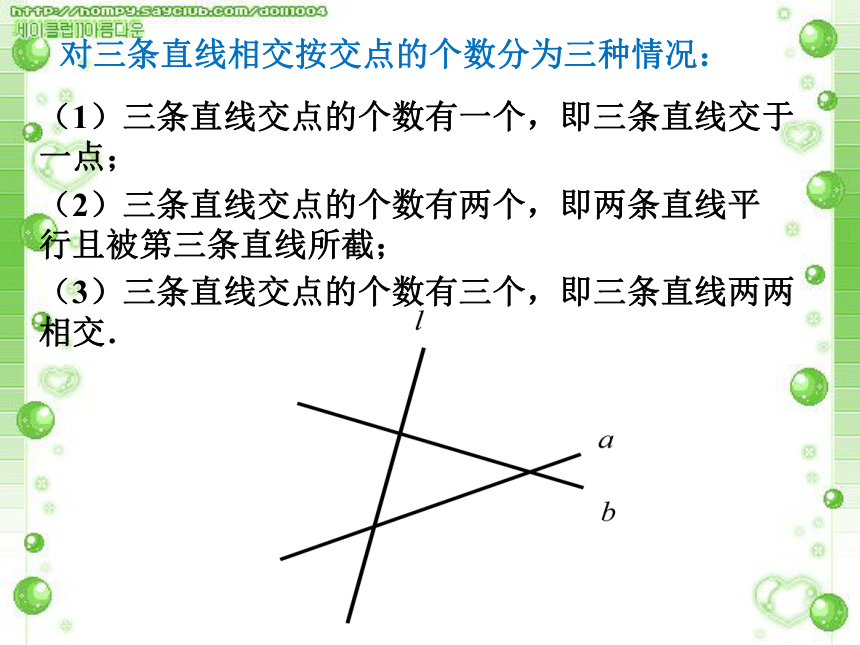
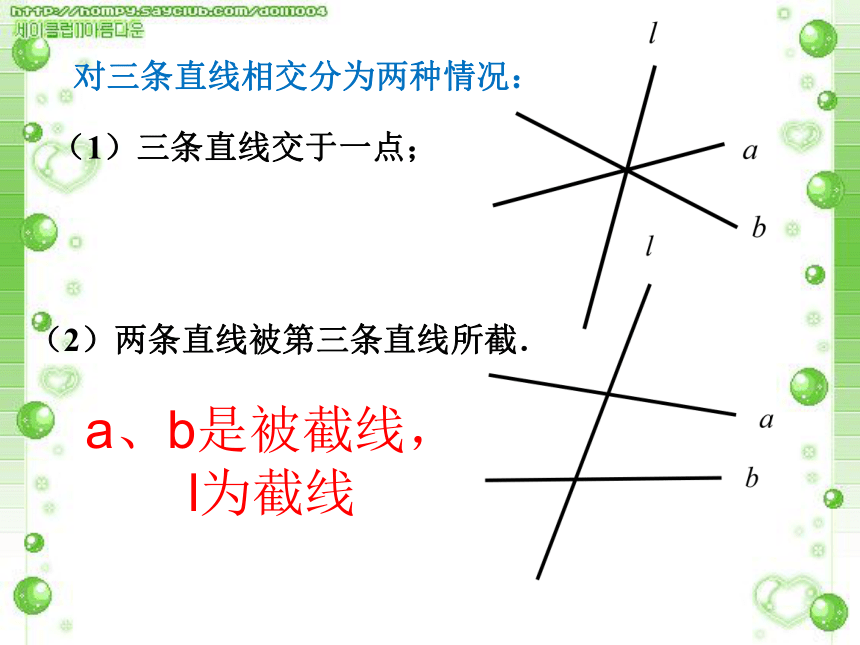
三条直线相交可以分为哪些情况?对三条直线相交按交点的个数分为三种情况:(1)三条直线交点的个数有一个,即三条直线交于一点; 对三条直线相交按交点的个数分为三种情况:(1)三条直线交点的个数有一个,即三条直线交于一点; (2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;对三条直线相交按交点的个数分为三种情况:(1)三条直线交点的个数有一个,即三条直线交于一点; (2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;(3)三条直线交点的个数有三个,即三条直线两两相交.对三条直线相交分为两种情况:(1)三条直线交于一点;(2)两条直线被第三条直线所截.a、b是被截线,l为截线问题3:观察图中的∠1和∠5,它们具有怎样的位置关系?如图,像∠1和∠5,两个角分别在直线AB、CD(被截线)的同一方,并且都在直线EF(截线)的同侧.具有这种位置关系的一对角叫做同位角.问题4:
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?(1)除了∠1和∠5是同位角,还有∠2和∠6,∠3和∠7, ∠4和∠8也构成同位角.(2)共有4对同位角.像字母F同位角问题5:观察图中的∠3和∠5,它们有怎样的位置关系?如图,像∠3和∠5,两个角都在直线AB、CD(被截线)之间,并且分别在直线EF(截线)两侧.具有这种位置关系的一对角叫做内错角.问题6:
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?(1)除了∠3和∠5是内错角,还有∠4和∠6 也构成内错角.(2)共有2对 内错角.内错角像字母Z问题7:
(1)如图,我们称∠3和∠6为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?如图,像∠3和∠6,两个角都在直线AB、CD(被截线)之间,并且都在直线EF(截线)的同一旁.具有这种位置关系的一对角叫做同旁内角.问题7:(2)你能找出图中还有哪几对角构成同旁内角?
(3)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?(1)除了∠4和∠5是同旁内角,还有∠3和∠6 也构成同旁内角.(2)共有2对 同旁内角.同旁内角像字母U在截线的同侧,在被截两直线的同旁在截线的同侧,在被截两直线之间在截线的两侧,在被截两直线之间都在截线的同侧都在被截两直线之间这三类角都是没有公共顶点的归纳同位角、内错角和同旁内角的特征:“F”“U”“Z” 1.上述三类角类似于对应角都是成对出现。不能说哪个角是同位角、内错角等。
2.解题之前要明确哪两条直线被哪条直线所截注意:试一试(2)若ED,BF被AB所截, 则∠1与∠2是_____ 。同位角(1)若ED,BC被AF所截, 则∠3与∠4 _____ 。内错角课堂练习1.看图填空(3)∠1与∠3是AB和AF被_____所截构成的_______。DE内错角(4)∠2与∠AFB是AB和AF被_____所截构成的_______。BC同旁内角(5)∠2与∠4是_____和_____被 BC所截构成的 ______ 。ABAF同位角2.请同学们指出下列各图中∠1与∠2的关系①内错角②同位角③同旁内角3、如图(1)∠1和∠2是直线 和 被直线—— 所截而成的内错角.(2)∠3和∠4是直线 和 被 所截,构成内错角.
(3)∠BAD与∠CDA是直线 和 被 所截,构成同旁内角.
(4)∠DCE与∠ABC是直线 和 被 所截,构成的同位角.能力提升ABDCACABDCADABDCBEADBCAB巩固练习1.如图,∠1和∠2不是同位角的是( )12121122(A)(B)(C)(D)abOMcabcEFMNabcEFMNabcD2.(1) ∠2与∠4是直线 和 被直线 所截而得的 _____ . (2)∠4与∠5是直
线____和____被直
线____所截而得的
_________.BCEFDE同位角DEBCEF同旁内角 3. 看图填空:
(1)若ED,BF被AB所截,
则∠ 1与 是同位角;
(2)若ED,BC被AF所截,
则∠3与 是内错角;
(3) ∠1与∠3是AB和AF被 所截
构成的 角
(4) ∠2 与∠4是 和 被BC
所截构成的 角。∠2∠4ED内错ABAF同位____________________________ABDEF1234例.如图,直线DE、BC被直线AB所截,
(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?∵∠1=∠4(已知),∠2=∠4(对顶角相等),
∴∠1=∠2.(等量代换)∵∠4+∠3=180o(邻补角定义)
∠1=∠4(已知)
∴∠1+∠3 =180o(等量代换)
∴∠1和∠3互补(补角定义)五、小结2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。(1)同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,我们要掌握他们的位置特征.1、找出下列各图中所有的同位角、内错角、同旁内角。解:(1) 同位角: ∠1和∠8, ∠2和∠5, ∠3和 ∠6, ∠4和∠7.
内错角: ∠1和∠6, ∠4和∠5.
同旁内角: ∠1和 ∠5, ∠4和 ∠6.
(2)同位角: ∠1和∠3,∠2和∠4.
同旁内角: ∠2和∠3.课后作业(1)(2)2.如图,直线DE、BC被直线AB所截。
(1)∠1与∠2、∠1与∠3、∠1与∠4各是什么角?(2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?答:(1) ∠1与∠2是内错角、∠1与∠3是同旁内角、∠1与∠4是
同位角。(2)如果∠1=∠4,由对顶角相等,得∠2=∠4。那么∠1=∠2。∵∠4与∠3互补;即∠4+∠3=180°又∵∠1=∠4,∴∠1+∠3=180°;即∠1与∠3互补。再见同学们的配合
1、垂线的定义。
2、垂线有什的性质?
3、什么叫点到直线的距离?垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.5.1.3同位角
内错角
同旁内角(1)了解同位角、内错角、同旁内角的概念.
(2)通过在图形中识别同位角、内错角、同旁内角,提高识图能力,体会分类的思想.
学习重点:
同位角、内错角、同旁内角的识别.学习目标:问题1:如图,直线AB与EF相交,你能说出其中的对顶角与邻补角吗?(一)复习引入对顶角:
∠1和∠3,∠2和∠4.邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.(二)探索与思考问题2:
三条直线相交可以分为哪些情况?对三条直线相交按交点的个数分为三种情况:(1)三条直线交点的个数有一个,即三条直线交于一点; 对三条直线相交按交点的个数分为三种情况:(1)三条直线交点的个数有一个,即三条直线交于一点; (2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;对三条直线相交按交点的个数分为三种情况:(1)三条直线交点的个数有一个,即三条直线交于一点; (2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;(3)三条直线交点的个数有三个,即三条直线两两相交.对三条直线相交分为两种情况:(1)三条直线交于一点;(2)两条直线被第三条直线所截.a、b是被截线,l为截线问题3:观察图中的∠1和∠5,它们具有怎样的位置关系?如图,像∠1和∠5,两个角分别在直线AB、CD(被截线)的同一方,并且都在直线EF(截线)的同侧.具有这种位置关系的一对角叫做同位角.问题4:
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?(1)除了∠1和∠5是同位角,还有∠2和∠6,∠3和∠7, ∠4和∠8也构成同位角.(2)共有4对同位角.像字母F同位角问题5:观察图中的∠3和∠5,它们有怎样的位置关系?如图,像∠3和∠5,两个角都在直线AB、CD(被截线)之间,并且分别在直线EF(截线)两侧.具有这种位置关系的一对角叫做内错角.问题6:
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?(1)除了∠3和∠5是内错角,还有∠4和∠6 也构成内错角.(2)共有2对 内错角.内错角像字母Z问题7:
(1)如图,我们称∠3和∠6为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?如图,像∠3和∠6,两个角都在直线AB、CD(被截线)之间,并且都在直线EF(截线)的同一旁.具有这种位置关系的一对角叫做同旁内角.问题7:(2)你能找出图中还有哪几对角构成同旁内角?
(3)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?(1)除了∠4和∠5是同旁内角,还有∠3和∠6 也构成同旁内角.(2)共有2对 同旁内角.同旁内角像字母U在截线的同侧,在被截两直线的同旁在截线的同侧,在被截两直线之间在截线的两侧,在被截两直线之间都在截线的同侧都在被截两直线之间这三类角都是没有公共顶点的归纳同位角、内错角和同旁内角的特征:“F”“U”“Z” 1.上述三类角类似于对应角都是成对出现。不能说哪个角是同位角、内错角等。
2.解题之前要明确哪两条直线被哪条直线所截注意:试一试(2)若ED,BF被AB所截, 则∠1与∠2是_____ 。同位角(1)若ED,BC被AF所截, 则∠3与∠4 _____ 。内错角课堂练习1.看图填空(3)∠1与∠3是AB和AF被_____所截构成的_______。DE内错角(4)∠2与∠AFB是AB和AF被_____所截构成的_______。BC同旁内角(5)∠2与∠4是_____和_____被 BC所截构成的 ______ 。ABAF同位角2.请同学们指出下列各图中∠1与∠2的关系①内错角②同位角③同旁内角3、如图(1)∠1和∠2是直线 和 被直线—— 所截而成的内错角.(2)∠3和∠4是直线 和 被 所截,构成内错角.
(3)∠BAD与∠CDA是直线 和 被 所截,构成同旁内角.
(4)∠DCE与∠ABC是直线 和 被 所截,构成的同位角.能力提升ABDCACABDCADABDCBEADBCAB巩固练习1.如图,∠1和∠2不是同位角的是( )12121122(A)(B)(C)(D)abOMcabcEFMNabcEFMNabcD2.(1) ∠2与∠4是直线 和 被直线 所截而得的 _____ . (2)∠4与∠5是直
线____和____被直
线____所截而得的
_________.BCEFDE同位角DEBCEF同旁内角 3. 看图填空:
(1)若ED,BF被AB所截,
则∠ 1与 是同位角;
(2)若ED,BC被AF所截,
则∠3与 是内错角;
(3) ∠1与∠3是AB和AF被 所截
构成的 角
(4) ∠2 与∠4是 和 被BC
所截构成的 角。∠2∠4ED内错ABAF同位____________________________ABDEF1234例.如图,直线DE、BC被直线AB所截,
(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?∵∠1=∠4(已知),∠2=∠4(对顶角相等),
∴∠1=∠2.(等量代换)∵∠4+∠3=180o(邻补角定义)
∠1=∠4(已知)
∴∠1+∠3 =180o(等量代换)
∴∠1和∠3互补(补角定义)五、小结2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。(1)同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,我们要掌握他们的位置特征.1、找出下列各图中所有的同位角、内错角、同旁内角。解:(1) 同位角: ∠1和∠8, ∠2和∠5, ∠3和 ∠6, ∠4和∠7.
内错角: ∠1和∠6, ∠4和∠5.
同旁内角: ∠1和 ∠5, ∠4和 ∠6.
(2)同位角: ∠1和∠3,∠2和∠4.
同旁内角: ∠2和∠3.课后作业(1)(2)2.如图,直线DE、BC被直线AB所截。
(1)∠1与∠2、∠1与∠3、∠1与∠4各是什么角?(2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?答:(1) ∠1与∠2是内错角、∠1与∠3是同旁内角、∠1与∠4是
同位角。(2)如果∠1=∠4,由对顶角相等,得∠2=∠4。那么∠1=∠2。∵∠4与∠3互补;即∠4+∠3=180°又∵∠1=∠4,∴∠1+∠3=180°;即∠1与∠3互补。再见同学们的配合
