6.1分类加法计数原理与分步乘法计数原理(共18张PPT)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 21:30:49 | ||
图片预览




文档简介
(共18张PPT)
1.了解分类加法计数原理与分步乘法计数原理及其意义.
2.会利用两个计数原理分析和解决一些简单的应用问题.
3.培养学生的数据分析能力.
第六章 计数原理
1 |分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案
中有n种不同的方法,那么完成这件事共有N=① m+n 种不同的方法.
推广:完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案
中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有
N=② m1+m2+…+mn 种不同的方法.
2 |分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方
法,那么完成这件事共有N=③ m×n 种不同的方法.
推广:完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方
法,……,做第n步有mn种不同的方法,那么完成这件事共有N=④ m1×m2×…×mn 种
不同的方法.
第六章 计数原理
3 |分类加法计数原理与分步乘法计数原理的比较与选择
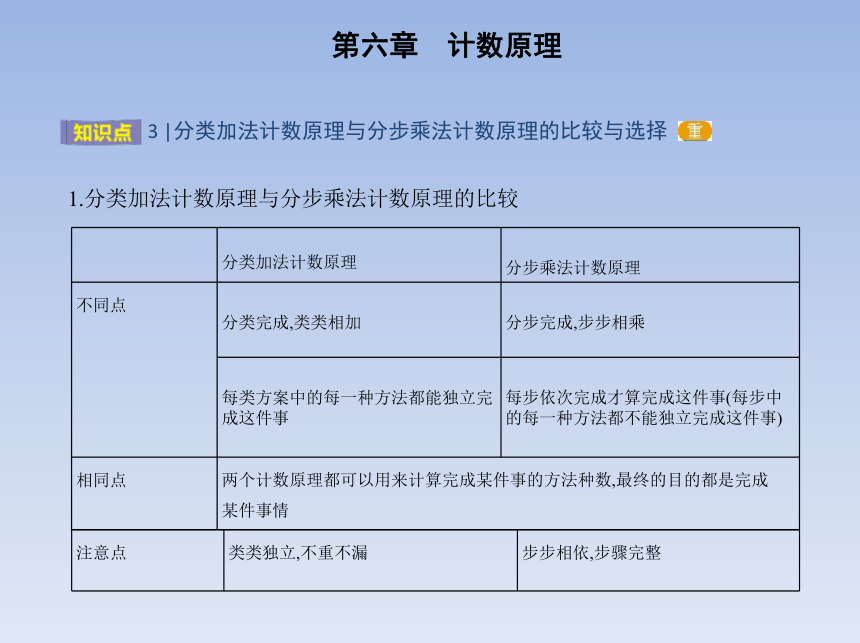
1.分类加法计数原理与分步乘法计数原理的比较
分类加法计数原理
分步乘法计数原理
不同点
分类完成,类类相加
分步完成,步步相乘
每类方案中的每一种方法都能独立完
成这件事
每步依次完成才算完成这件事(每步中的每一种方法都不能独立完成这件事)
相同点 两个计数原理都可以用来计算完成某件事的方法种数,最终的目的都是完成
某件事情
注意点 类类独立,不重不漏 步步相依,步骤完整
第六章 计数原理
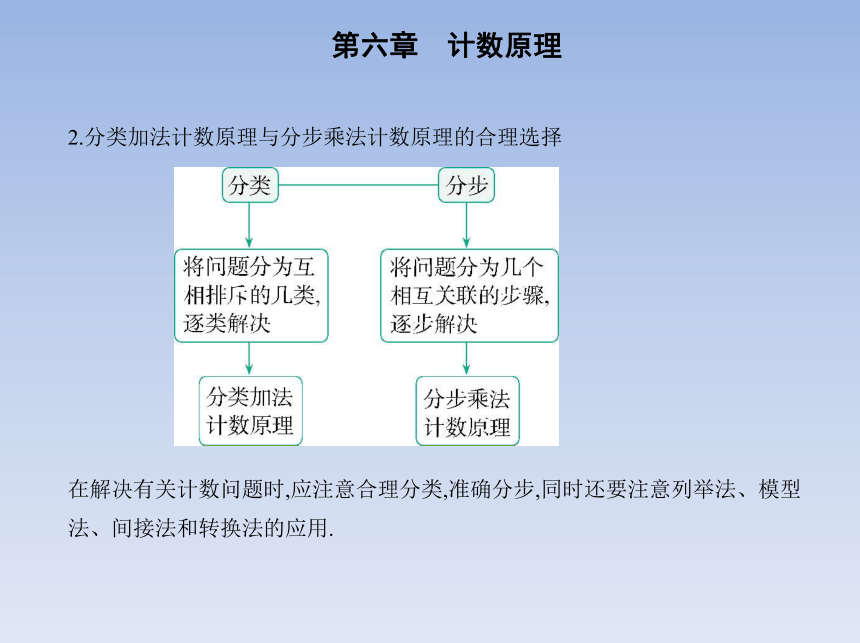
2.分类加法计数原理与分步乘法计数原理的合理选择
在解决有关计数问题时,应注意合理分类,准确分步,同时还要注意列举法、模型
法、间接法和转换法的应用.
第六章 计数原理
1.在分类加法计数原理中,两类不同方案中的方法可以相同. ( )
2.在分类加法计数原理中,每类不同方案中的方法都能完成这件事. ( √ )
3.在分步乘法计数原理中,任何一个单独的步骤都能完成这件事. ( )
4.把10个苹果分成三份,要求每份至少有1个,至多有5个,则有4种不同分法. ( √ )
若其中一份有1个,则另两份分别有4个、5个,有1种分法;若其中一份有2个,则另两
份分别有3个、5个,或4个、4个,有2种分法;若其中一份有3个,则另两份分别有3
个、4个,有1种分法.所以共有1+2+1=4种分法.
5.在一次运动会上有四项比赛,冠军仅在甲、乙、丙三人中产生,那么不同的夺冠
情况共有43种. ( )
因为每个项目的冠军都有3种可能的情况,所以由分步乘法计数原理知,共有34种
不同的夺冠情况.
判断正误,正确的画“√”,错误的画“ ”.
第六章 计数原理
6.三个袋子内共装有18个不同的小球,一个装有5个白色小球,一个装有6个黑色小
球,一个装有7个红色小球,若每次从中取两个不同颜色的小球,则共有36种不同的
取法. ( )
分为三类:一类是取白球、黑球,有5×6=30种取法;一类是取白球、红球,有5×7=35
种取法;一类是取黑球、红球,有6×7=42种取法,所以由分类加法计数原理知,共有3
0+35+42=107种不同的取法.
第六章 计数原理
1 |两个计数原理的选择与应用
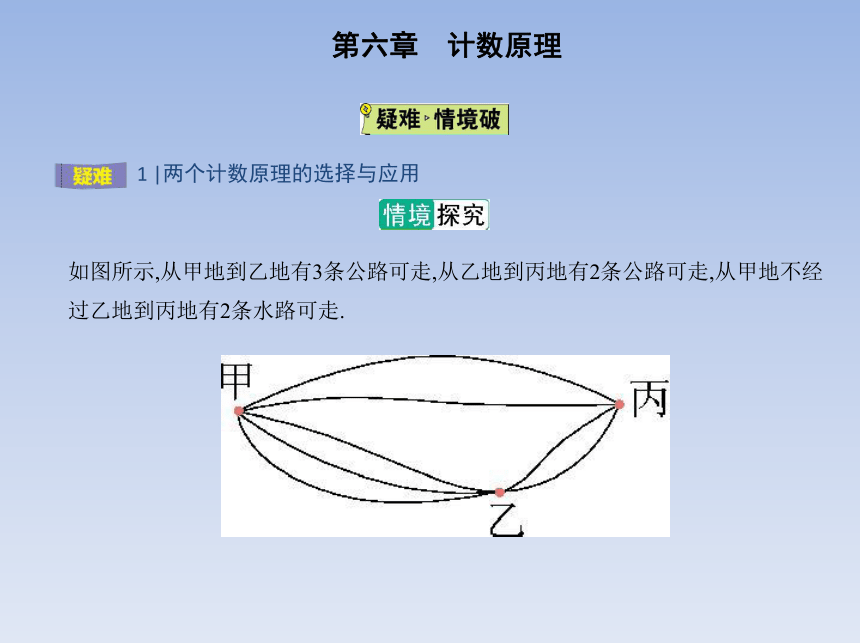
如图所示,从甲地到乙地有3条公路可走,从乙地到丙地有2条公路可走,从甲地不经
过乙地到丙地有2条水路可走.
第六章 计数原理
1.从甲地经乙地到丙地的走法有多少种
提示:根据分步乘法计数原理,可得从甲地经乙地到丙地的走法共有3×2=6种.
2.从甲地到丙地的走法一共有多少种
提示:根据分类加法计数原理,可得从甲地到丙地的走法共有6+2=8种.
第六章 计数原理
两个计数原理在解决计数问题中的应用
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析,分清是
分类还是分步.
第六章 计数原理
类中有步,步中有类
从A→D共有m1×(m2+m3+m4)×m5种方法.
从A→B共有(m1×m2×m3+m4×m5)种方法.
“类”用“+”连接,“步”用“×”连接,“类”独立,“步”连续,“类”标志一件
事的完成,“步”则缺一不可.
第六章 计数原理
应用两个计数原理的常用方法
(1)当涉及元素数目不大时,一般选用列举法、树状图法、框图法或图表法.
(2)当涉及元素数目很大时,一般有两种方法:
①直接法:直接使用分类加法计数原理或分步乘法计数原理.
②间接法:先去掉限制条件,计算方法总数,然后减去所有不符合条件的方法数即可.
第六章 计数原理
在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另外2名
既会下象棋又会下围棋.现从这7人中选2人分别参加象棋比赛和围棋比赛,共有多
少种不同的选法
解析 分四类:第1类,从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名只
会下围棋的学生中选1名参加围棋比赛,有3×2=6种选法;
第2类,从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名既会下象棋又会
下围棋的学生中选1名参加围棋比赛,有3×2=6种选法;
第3类,从2名只会下围棋的学生中选1名参加围棋比赛,同时从2名既会下象棋又会
下围棋的学生中选1名参加象棋比赛,有2×2=4种选法;
第4类,从2名既会下象棋又会下围棋的学生中各选1名分别参加象棋比赛和围棋比
赛,有2×1=2种选法.
第六章 计数原理
故不同的选法共有6+6+4+2=18种.
方法总结 在解决实际问题的过程中,并不一定是单一的分类或分步,而是可能同
时应用两个计数原理,即分类时,每类的方法数可能要分步完成;分步时,每步的方法
数可能会采取分类的思想解决.另外,具体问题是先分类后分步,还是先分步后分类,
应视问题的特点而定.解题时经常是两个计数原理交叉使用,分类的关键在于要做
到“不重不漏”,分步的关键在于要正确设计分步的程序,即合理分类,准确分步.
第六章 计数原理
若直线方程Ax+By=0中的A,B可以从0,1,2,3,5这5个数字中任取2个不同的数字,求该
方程所表示的不同直线的条数.
思路点拨
以A,B中是否有数字0为标准进行分类计数,或利用排除法求解.
解析 解法一:分两类.
第一类:当A,B中有一个为0时,方程表示直线x=0或y=0,共2条不同的直线.
第二类:当A,B都不为0时,确定直线Ax+By=0需要分两步完成.
第一步,确定A的值,有4种不同的方法.
第二步,确定B的值,有3种不同的方法.
所以该方程所表示的不同直线共有2+4×3=14条.
第六章 计数原理
解法二(间接法):分两步.
第一步:确定A的值,有5种不同的方法.
第二步:确定B的值,有4种不同的方法.
根据分步乘法计数原理,可以确定5×4=20条直线.
在这20条直线中,当A=0,B=1,2,3,5时,表示同一直线y=0;当B=0,A=1,2,3,5时,表示同
一直线x=0,即有6条直线是重复计数的.故该方程所表示的不同直线有20-6=14条.
名师点评 当问题从正面考虑情况比较多,而从反面考虑情况较少且容易计算时,
宜采用排除法,即先求出方法总数,再减去不符合条件或重复计数的方法数.排除法
体现了“正难则反”的思想.
第六章 计数原理
2 |涂色问题
涂色问题是计数原理应用的典型问题,一般是指求用几种不同颜色给已知图形的
不同区域(或点)涂色,共有几种涂法的问题.涂色本身就是策略的一个运用过程.涂
色时需要关注图形特征:区域的个数、区域的相邻情况、图形形状等.这些特征都
有可能使分类的标准、分步的过程不同.涂色问题大致有两种解决方案:(1)选择正
确的涂色顺序,按步骤逐一涂色,应用分步乘法计数原理进行计算;(2)先根据涂色时
所用颜色种数的多少进行分类处理,再在每一类的涂色方案的计算中应用分步乘
法计数原理,最后根据分类加法计数原理对每一类的涂色方法数求和,即得到最终
的涂色方法数.
第六章 计数原理
将红、黄、绿、黑四种颜色涂在如图所示的五个区域中,若要求相邻的两个区域
的颜色都不相同,则有多少种不同的涂色方法
第六章 计数原理
解析 解法一:①当B与D同色时,不同的涂色方法有4×3×2×1×2=48种;
②当B与D不同色时,不同的涂色方法有4×3×2×1×1=24种.
故共有48+24=72种不同的涂色方法.
解法二:按涂色时所用颜色种数分类:
第一类,用4种颜色,此时B,D或A,E同色,则共有2×4×3×2×1=48种不同的涂色方法;
第二类,用3种颜色,此时B,D同色,A,E同色,
先从4种颜色中取3种,再涂色,
共有4×3×2×1=24种不同的涂色方法.
由分类加法计数原理知,共有48+24=72种不同的涂色方法.
规律方法 求解涂色(种植)问题一般是直接利用两个计数原理求解,常用方法如下:
(1)根据区域的不同,以区域为主分步计数,用分步乘法计数原理分析;
(2)以颜色(种植作物)为主分类讨论,适用于“区域、点、线段”问题,用分类加法
计数原理分析.
第六章 计数原理
1.了解分类加法计数原理与分步乘法计数原理及其意义.
2.会利用两个计数原理分析和解决一些简单的应用问题.
3.培养学生的数据分析能力.
第六章 计数原理
1 |分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案
中有n种不同的方法,那么完成这件事共有N=① m+n 种不同的方法.
推广:完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案
中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有
N=② m1+m2+…+mn 种不同的方法.
2 |分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方
法,那么完成这件事共有N=③ m×n 种不同的方法.
推广:完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方
法,……,做第n步有mn种不同的方法,那么完成这件事共有N=④ m1×m2×…×mn 种
不同的方法.
第六章 计数原理
3 |分类加法计数原理与分步乘法计数原理的比较与选择
1.分类加法计数原理与分步乘法计数原理的比较
分类加法计数原理
分步乘法计数原理
不同点
分类完成,类类相加
分步完成,步步相乘
每类方案中的每一种方法都能独立完
成这件事
每步依次完成才算完成这件事(每步中的每一种方法都不能独立完成这件事)
相同点 两个计数原理都可以用来计算完成某件事的方法种数,最终的目的都是完成
某件事情
注意点 类类独立,不重不漏 步步相依,步骤完整
第六章 计数原理
2.分类加法计数原理与分步乘法计数原理的合理选择
在解决有关计数问题时,应注意合理分类,准确分步,同时还要注意列举法、模型
法、间接法和转换法的应用.
第六章 计数原理
1.在分类加法计数原理中,两类不同方案中的方法可以相同. ( )
2.在分类加法计数原理中,每类不同方案中的方法都能完成这件事. ( √ )
3.在分步乘法计数原理中,任何一个单独的步骤都能完成这件事. ( )
4.把10个苹果分成三份,要求每份至少有1个,至多有5个,则有4种不同分法. ( √ )
若其中一份有1个,则另两份分别有4个、5个,有1种分法;若其中一份有2个,则另两
份分别有3个、5个,或4个、4个,有2种分法;若其中一份有3个,则另两份分别有3
个、4个,有1种分法.所以共有1+2+1=4种分法.
5.在一次运动会上有四项比赛,冠军仅在甲、乙、丙三人中产生,那么不同的夺冠
情况共有43种. ( )
因为每个项目的冠军都有3种可能的情况,所以由分步乘法计数原理知,共有34种
不同的夺冠情况.
判断正误,正确的画“√”,错误的画“ ”.
第六章 计数原理
6.三个袋子内共装有18个不同的小球,一个装有5个白色小球,一个装有6个黑色小
球,一个装有7个红色小球,若每次从中取两个不同颜色的小球,则共有36种不同的
取法. ( )
分为三类:一类是取白球、黑球,有5×6=30种取法;一类是取白球、红球,有5×7=35
种取法;一类是取黑球、红球,有6×7=42种取法,所以由分类加法计数原理知,共有3
0+35+42=107种不同的取法.
第六章 计数原理
1 |两个计数原理的选择与应用
如图所示,从甲地到乙地有3条公路可走,从乙地到丙地有2条公路可走,从甲地不经
过乙地到丙地有2条水路可走.
第六章 计数原理
1.从甲地经乙地到丙地的走法有多少种
提示:根据分步乘法计数原理,可得从甲地经乙地到丙地的走法共有3×2=6种.
2.从甲地到丙地的走法一共有多少种
提示:根据分类加法计数原理,可得从甲地到丙地的走法共有6+2=8种.
第六章 计数原理
两个计数原理在解决计数问题中的应用
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析,分清是
分类还是分步.
第六章 计数原理
类中有步,步中有类
从A→D共有m1×(m2+m3+m4)×m5种方法.
从A→B共有(m1×m2×m3+m4×m5)种方法.
“类”用“+”连接,“步”用“×”连接,“类”独立,“步”连续,“类”标志一件
事的完成,“步”则缺一不可.
第六章 计数原理
应用两个计数原理的常用方法
(1)当涉及元素数目不大时,一般选用列举法、树状图法、框图法或图表法.
(2)当涉及元素数目很大时,一般有两种方法:
①直接法:直接使用分类加法计数原理或分步乘法计数原理.
②间接法:先去掉限制条件,计算方法总数,然后减去所有不符合条件的方法数即可.
第六章 计数原理
在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另外2名
既会下象棋又会下围棋.现从这7人中选2人分别参加象棋比赛和围棋比赛,共有多
少种不同的选法
解析 分四类:第1类,从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名只
会下围棋的学生中选1名参加围棋比赛,有3×2=6种选法;
第2类,从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名既会下象棋又会
下围棋的学生中选1名参加围棋比赛,有3×2=6种选法;
第3类,从2名只会下围棋的学生中选1名参加围棋比赛,同时从2名既会下象棋又会
下围棋的学生中选1名参加象棋比赛,有2×2=4种选法;
第4类,从2名既会下象棋又会下围棋的学生中各选1名分别参加象棋比赛和围棋比
赛,有2×1=2种选法.
第六章 计数原理
故不同的选法共有6+6+4+2=18种.
方法总结 在解决实际问题的过程中,并不一定是单一的分类或分步,而是可能同
时应用两个计数原理,即分类时,每类的方法数可能要分步完成;分步时,每步的方法
数可能会采取分类的思想解决.另外,具体问题是先分类后分步,还是先分步后分类,
应视问题的特点而定.解题时经常是两个计数原理交叉使用,分类的关键在于要做
到“不重不漏”,分步的关键在于要正确设计分步的程序,即合理分类,准确分步.
第六章 计数原理
若直线方程Ax+By=0中的A,B可以从0,1,2,3,5这5个数字中任取2个不同的数字,求该
方程所表示的不同直线的条数.
思路点拨
以A,B中是否有数字0为标准进行分类计数,或利用排除法求解.
解析 解法一:分两类.
第一类:当A,B中有一个为0时,方程表示直线x=0或y=0,共2条不同的直线.
第二类:当A,B都不为0时,确定直线Ax+By=0需要分两步完成.
第一步,确定A的值,有4种不同的方法.
第二步,确定B的值,有3种不同的方法.
所以该方程所表示的不同直线共有2+4×3=14条.
第六章 计数原理
解法二(间接法):分两步.
第一步:确定A的值,有5种不同的方法.
第二步:确定B的值,有4种不同的方法.
根据分步乘法计数原理,可以确定5×4=20条直线.
在这20条直线中,当A=0,B=1,2,3,5时,表示同一直线y=0;当B=0,A=1,2,3,5时,表示同
一直线x=0,即有6条直线是重复计数的.故该方程所表示的不同直线有20-6=14条.
名师点评 当问题从正面考虑情况比较多,而从反面考虑情况较少且容易计算时,
宜采用排除法,即先求出方法总数,再减去不符合条件或重复计数的方法数.排除法
体现了“正难则反”的思想.
第六章 计数原理
2 |涂色问题
涂色问题是计数原理应用的典型问题,一般是指求用几种不同颜色给已知图形的
不同区域(或点)涂色,共有几种涂法的问题.涂色本身就是策略的一个运用过程.涂
色时需要关注图形特征:区域的个数、区域的相邻情况、图形形状等.这些特征都
有可能使分类的标准、分步的过程不同.涂色问题大致有两种解决方案:(1)选择正
确的涂色顺序,按步骤逐一涂色,应用分步乘法计数原理进行计算;(2)先根据涂色时
所用颜色种数的多少进行分类处理,再在每一类的涂色方案的计算中应用分步乘
法计数原理,最后根据分类加法计数原理对每一类的涂色方法数求和,即得到最终
的涂色方法数.
第六章 计数原理
将红、黄、绿、黑四种颜色涂在如图所示的五个区域中,若要求相邻的两个区域
的颜色都不相同,则有多少种不同的涂色方法
第六章 计数原理
解析 解法一:①当B与D同色时,不同的涂色方法有4×3×2×1×2=48种;
②当B与D不同色时,不同的涂色方法有4×3×2×1×1=24种.
故共有48+24=72种不同的涂色方法.
解法二:按涂色时所用颜色种数分类:
第一类,用4种颜色,此时B,D或A,E同色,则共有2×4×3×2×1=48种不同的涂色方法;
第二类,用3种颜色,此时B,D同色,A,E同色,
先从4种颜色中取3种,再涂色,
共有4×3×2×1=24种不同的涂色方法.
由分类加法计数原理知,共有48+24=72种不同的涂色方法.
规律方法 求解涂色(种植)问题一般是直接利用两个计数原理求解,常用方法如下:
(1)根据区域的不同,以区域为主分步计数,用分步乘法计数原理分析;
(2)以颜色(种植作物)为主分类讨论,适用于“区域、点、线段”问题,用分类加法
计数原理分析.
第六章 计数原理
