6.2.1排列 6.2.2排列数 课件(共23张PPT)
文档属性
| 名称 | 6.2.1排列 6.2.2排列数 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 21:07:10 | ||
图片预览








文档简介
(共23张PPT)
6.2 排列与组合
6.2.1 排列
6.2.2 排列数
1.通过实例理解排列的概念.
2.能利用计数原理推导排列数公式.
3.掌握几种有限制条件的排列,能应用排列数公式解决一些简单的实际问题.
第六章 计数原理
1 |排列、排列数与排列数公式
1.从n个不同元素中取出m(m≤n)个元素,并按照① 一定的顺序 排成一列,叫做
从n个不同元素中取出m个元素的一个排列.
2.从n个不同元素中取出m(m≤n)个元素的所有不同排列的② 个数 ,叫做从n个
不同元素中取出m个元素的排列数,用符号③ 表示.
3.排列数公式: =④ n(n-1)(n-2)…(n-m+1) (m,n∈N*,m≤n).
第六章 计数原理
2 |全排列、阶乘的概念及相关结论
1.把n个不同的元素⑤ 全部取出 的一个排列,叫做n个元素的一个全排列,记作
⑥ .
2.正整数1到n的连乘积,叫做n的阶乘,用⑦ n! 表示.
3.阶乘的相关结论
(1)规定:0!=⑧ 1 .
(2) =⑨ n! (n∈N*).
(3)排列数公式的另一种形式: =⑩ (m,n∈N*,m≤n).
第六章 计数原理
3 |处理排列问题的常用方法
对于排列问题,从解题途径上看有直接法和间接法.
从解题策略上看,有元素分析法和位置分析法.
从解题技巧上看,有捆绑法和插空法.
第六章 计数原理
1.若组成两个排列的元素相同,则这两个排列是相同的. ( )
组成两个排列的元素的排列顺序不相同时,这两个排列是不相同的.
2.a,b,c与b,a,c是同一个排列. ( )
3.排列数公式 = 中m≠n. ( )
4.4×5×6×…×(n-1)×n= ,其中n∈N*,n≥4. ( √ )
5.5个人站成一排,其中甲、乙两人不相邻的排法可列式为 - . ( √ )
利用插空法可列式为 ;利用间接法可列式为 - .
判断正误,正确的画“√”,错误的画“ ”.
第六章 计数原理
1 |排列数及其运算
1.“排列”与“排列数”是两个不同的概念.排列是指“从n个不同元素中取出m
(m≤n)个元素,并按照一定的顺序排成一列”,这不是一个数;排列数是指“从n个不
同元素中取出m(m≤n)个元素的所有不同排列的个数”,这是一个数.
2.规定:0!=1,不按阶乘的含义作解释.
在排列数公式 =n(n-1)…(n-m+1)中,n,m要满足的条件是n,m∈N*,m≤n.
3.排列数的性质: =n =m + .
第六章 计数原理
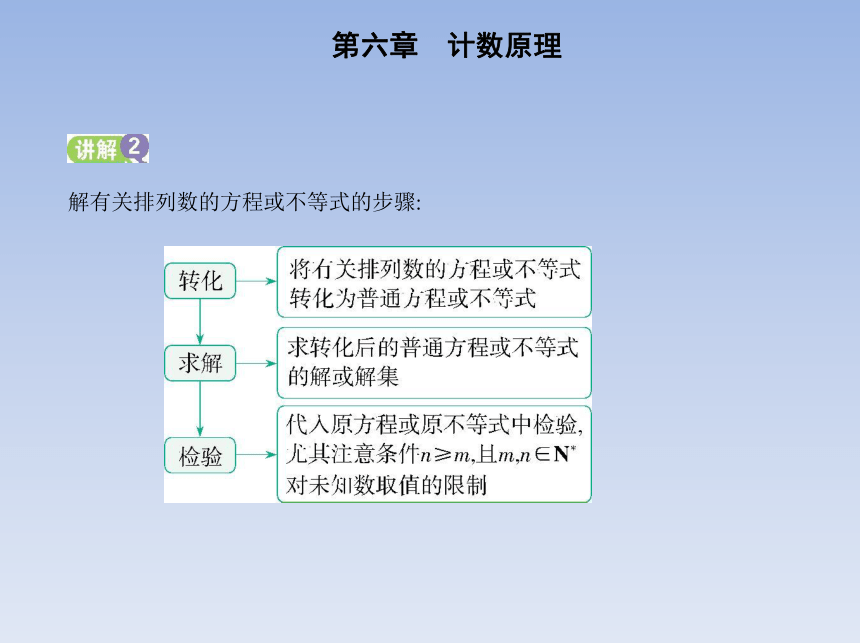
解有关排列数的方程或不等式的步骤:
第六章 计数原理
(1)用排列数表示(55-n)(56-n)…(69-n)(n∈N*且n<55);
(2)计算 ;
(3)化简求值:
①1!+2×2!+3×3!+…+n×n!(n∈N*);
② + + +…+ (n≥2且n∈N*);
(4)解不等式: >6 .
第六章 计数原理
解析 (1)∵55-n,56-n,…,69-n中最大的数为69-n,且共有(69-n)-(55-n)+1=15个正整
数,
∴(55-n)(56-n)…(69-n)= .
(2) =
= =3.
(3)①原式=(2!-1)+(3!-2!)+(4!-3!)+…+[(n+1)!-n!]=(n+1)!-1.
②∵ = - ,∴ + + +…+ = + + +…+ =1- .
第六章 计数原理
(4)易知 ∴2原不等式可化为 > ,其中2化简得(11-x)(10-x)>6,即x2-21x+104>0,
∴(x-8)(x-13)>0,解得x<8或x>13.
∵2故x=3,4,5,6,7,∴原不等式的解集为{3,4,5,6,7}.
方法总结 (1)排列数公式的乘积的形式适用于求值和当m较小时的含排列数的方
程和不等式问题.
(2)排列数公式的阶乘的形式主要用于与排列数有关的证明、解方程和不等式等
问题,具体应用时注意提取公因式,可以简化计算.
第六章 计数原理
2 |有限制条件的排队问题
“在”与“不在”的问题
解决“在”与“不在”的问题,常用的方法是特殊位置分析法、特殊元素分析法.
若以位置为主,则需先满足特殊位置的要求,再处理其他位置,若有两个及以上的约
束条件,则在考虑一个约束条件的同时要兼顾其他条件;若以元素为主,则需先满足
特殊元素的要求,再处理其他的元素.当直接求解困难时,可考虑用间接法求解,即先
不考虑限制条件,计算出排列总数,再减去不符合要求的排列数.
第六章 计数原理
“相邻”与“不相邻”问题
1.“捆绑法”解决相邻问题
解决相邻问题一般用“捆绑法”.将n个不同的元素排成一列,其中k(k≤n)个元素排
在相邻的位置上,求不同排法的种数的方法如下:(1)先将这k个元素“捆绑”在一
起,看成一个整体;(2)把这个整体当成一个元素与其他元素一起排列,有 种排
法;(3)“松绑”,即将“捆绑”在一起的元素进行内部排列,其排列方法有 种;(4)
由分步乘法计数原理知,符合条件的排法有 种.
第六章 计数原理
2.“插空法”解决不相邻问题
解决不相邻问题通常用“插空法”.将n个不同的元素排成一列,其中k 当n为奇数
时,k≤ ;当n为偶数时,k≤ 个元素互不相邻,求不同排法的种数的方法如下:
(1)将没有不相邻要求的(n-k)个元素排成一排,其排列方法有 种;(2)将要求两两
不相邻的k个元素插入(n-k+1)个空隙中,相当于从(n-k+1)个空隙中选出k个分别分配
给两两不相邻的k个元素,其排列方法有 种;(3)根据分步乘法计数原理知,符合
条件的排法有 种.
第六章 计数原理
“定序”问题
在排列问题中,某些元素在题意中已排定了顺序,对这些元素进行排列时,不再考虑
其顺序.在具体的计算过程中,可采用“除阶乘法”解决,即n个元素的全排列中有m
(m≤n)个元素的顺序固定,则满足题意的排法有 种.
第六章 计数原理
7名师生站成一排照相留念,其中老师1人,男学生4人,女学生2人.分别求满足下
列情况的不同站法的种数.
(1)老师甲必须站在中间或两端;
(2)2名女学生必须相邻而站;
(3)4名男学生互不相邻;
(4)若4名男学生身高都不等,按从高到低的顺序站.
第六章 计数原理
解析 (1)先考虑甲有 种站法,再考虑其余6人全排列,故不同站法的种数为
=2 160.
(2)2名女学生相邻而站有 种站法,视为一个整体并与其余5人全排列,有 种排
法,所以不同站法的种数为 =1 440.
(3)先站老师和女学生,有 种站法,再在老师和女学生站位的空(含两端)中插入男
学生,每空一人,则插入方法有 种,所以不同站法的种数为 =144.
(4)在7人全排列的所有站法中,4名男学生不考虑身高顺序的站法有 种,而从高到
低顺序站有从左到右和从右到左2种,所以不同站法的种数为2× =420.
第六章 计数原理
元宵节灯展后,如图悬挂的6盏不同的花灯需要取下,每次取1盏,共有 种不
同取法.(用数字作答)
第六章 计数原理
思路点拨
将问题转化为六个元素进行排列,而每一串的2盏花灯都有顺序,自下而上,所以是
排列中的“定序”问题.
解析 先将6盏花灯全排列共有 种排法,因为取花灯时每次只能取1盏,且每串花
灯必须先取下面的花灯,即每串2盏花灯取下的顺序确定,所以取下6盏不同的花灯,
每次取1盏,共有 = =90种不同取法.
答案 90
第六章 计数原理
3 |与数字有关的排列问题
数字排列问题的本质是“元素”占“位置”问题,有限制条件的排列问题的限制
条件主要表现在某元素不排在某个位置上或某个位置不排某些元素,解决该类排
列问题的主要方法是按照“优先”原则,即优先排特殊元素或优先满足特殊位置,
若一个位置安排的元素影响到另一个位置的元素个数时,应分类讨论.
含有数字“0”的排列问题中,有些隐含了数字“0”不能在首位的条件,应将其视
为有限制条件的元素优先进行排列.若在一个题目中,除了数字“0”以外还有其他
受限制的数字,则应考虑受限制的数字对位置的选择会不会影响数字“0”对位置
的选择,若有影响,则应分类讨论.
第六章 计数原理
从分别印有数字0,3,5,7,9的5张卡片中,任意抽出3张组成三位数.
(1)求可以组成多少个大于500的三位数;
(2)求可以组成多少个是5的倍数的三位数;
(3)若印有9的卡片,既可以当9用,也可以当6用,求可以组成多少个三位数.
思路点拨
(1)从首位大于或等于5进行分析.(2)从个位为0或5入手.(3)对特殊卡片9分被抽取和
未被抽取两种情况进行分析,当被抽取时又可以作为数字6用.
解析 (1)百位可以从5,7,9三张卡片中任取一张,十位和个位则可从剩下的卡片中
任取,所以可以组成大于500的三位数的个数为 =3×4×3=36.
(2)分两种情况:若个位为0,则十位和百位可从3,5,7,9中任取,有 =12个;若个位为5,
则百位只能从3,7,9中任取一张,十位再从剩下的3张卡片中任取一张,所以有 =
9个.
第六章 计数原理
所以可以组成12+9=21个是5的倍数的三位数.
(3)分三种情况:若卡片9没有被抽取,则这样的三位数有 =18个;若卡片9被抽取,
且0未被抽取,则这样的三位数有3 ×2=36个;若卡片9被抽取,且0被抽取,则这样的
三位数有2×3×2 =24个.
所以这样的三位数共有18+36+24=78个.
第六章 计数原理
用0,1,2,3,4,5这六个数字可以组成多少个:
(1)无重复数字且个位数字不是5的六位数
(2)无重复数字且比1 325大的四位数
(3)无重复数字的六位数 若这些六位数按从小到大的顺序排成一列,则240 135是该
列数的第几项
解析 (1)解法一:间接法.
0在十万位的六位数或5在个位的六位数都有 个,0在十万位且5在个位的六位数
有 个.
故符合题意的六位数共有 -2 + =504个.
第六章 计数原理
解法二:直接法.
十万位数字的排法因个位上数字为0与不为0而有所不同,因此需分两类:
第一类:当个位数字为0时,符合题意的六位数有 个;
第二类:当个位数字不为0时,符合题意的六位数有 个.
故符合题意的六位数共有 + =504个.
(2)符合题意的四位数可分为三类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共4 个;
第二类:形如14□□,15□□,共有2 个;
第三类:形如134□,135□,共有2 个.
由分类加法计数原理知,无重复数字且比1 325大的四位数共有4 +2 +2 =270个.
(3)符合题意的六位数共有 - =600个.由于是六位数,故十万位不能为0,则十万位
为1的有 个,十万位为2,万位上为0或1或3的共有3 个,∵ +3 +1=193,∴240 1
35是该列数的第193项.
第六章 计数原理
6.2 排列与组合
6.2.1 排列
6.2.2 排列数
1.通过实例理解排列的概念.
2.能利用计数原理推导排列数公式.
3.掌握几种有限制条件的排列,能应用排列数公式解决一些简单的实际问题.
第六章 计数原理
1 |排列、排列数与排列数公式
1.从n个不同元素中取出m(m≤n)个元素,并按照① 一定的顺序 排成一列,叫做
从n个不同元素中取出m个元素的一个排列.
2.从n个不同元素中取出m(m≤n)个元素的所有不同排列的② 个数 ,叫做从n个
不同元素中取出m个元素的排列数,用符号③ 表示.
3.排列数公式: =④ n(n-1)(n-2)…(n-m+1) (m,n∈N*,m≤n).
第六章 计数原理
2 |全排列、阶乘的概念及相关结论
1.把n个不同的元素⑤ 全部取出 的一个排列,叫做n个元素的一个全排列,记作
⑥ .
2.正整数1到n的连乘积,叫做n的阶乘,用⑦ n! 表示.
3.阶乘的相关结论
(1)规定:0!=⑧ 1 .
(2) =⑨ n! (n∈N*).
(3)排列数公式的另一种形式: =⑩ (m,n∈N*,m≤n).
第六章 计数原理
3 |处理排列问题的常用方法
对于排列问题,从解题途径上看有直接法和间接法.
从解题策略上看,有元素分析法和位置分析法.
从解题技巧上看,有捆绑法和插空法.
第六章 计数原理
1.若组成两个排列的元素相同,则这两个排列是相同的. ( )
组成两个排列的元素的排列顺序不相同时,这两个排列是不相同的.
2.a,b,c与b,a,c是同一个排列. ( )
3.排列数公式 = 中m≠n. ( )
4.4×5×6×…×(n-1)×n= ,其中n∈N*,n≥4. ( √ )
5.5个人站成一排,其中甲、乙两人不相邻的排法可列式为 - . ( √ )
利用插空法可列式为 ;利用间接法可列式为 - .
判断正误,正确的画“√”,错误的画“ ”.
第六章 计数原理
1 |排列数及其运算
1.“排列”与“排列数”是两个不同的概念.排列是指“从n个不同元素中取出m
(m≤n)个元素,并按照一定的顺序排成一列”,这不是一个数;排列数是指“从n个不
同元素中取出m(m≤n)个元素的所有不同排列的个数”,这是一个数.
2.规定:0!=1,不按阶乘的含义作解释.
在排列数公式 =n(n-1)…(n-m+1)中,n,m要满足的条件是n,m∈N*,m≤n.
3.排列数的性质: =n =m + .
第六章 计数原理
解有关排列数的方程或不等式的步骤:
第六章 计数原理
(1)用排列数表示(55-n)(56-n)…(69-n)(n∈N*且n<55);
(2)计算 ;
(3)化简求值:
①1!+2×2!+3×3!+…+n×n!(n∈N*);
② + + +…+ (n≥2且n∈N*);
(4)解不等式: >6 .
第六章 计数原理
解析 (1)∵55-n,56-n,…,69-n中最大的数为69-n,且共有(69-n)-(55-n)+1=15个正整
数,
∴(55-n)(56-n)…(69-n)= .
(2) =
= =3.
(3)①原式=(2!-1)+(3!-2!)+(4!-3!)+…+[(n+1)!-n!]=(n+1)!-1.
②∵ = - ,∴ + + +…+ = + + +…+ =1- .
第六章 计数原理
(4)易知 ∴2
∴(x-8)(x-13)>0,解得x<8或x>13.
∵2
方法总结 (1)排列数公式的乘积的形式适用于求值和当m较小时的含排列数的方
程和不等式问题.
(2)排列数公式的阶乘的形式主要用于与排列数有关的证明、解方程和不等式等
问题,具体应用时注意提取公因式,可以简化计算.
第六章 计数原理
2 |有限制条件的排队问题
“在”与“不在”的问题
解决“在”与“不在”的问题,常用的方法是特殊位置分析法、特殊元素分析法.
若以位置为主,则需先满足特殊位置的要求,再处理其他位置,若有两个及以上的约
束条件,则在考虑一个约束条件的同时要兼顾其他条件;若以元素为主,则需先满足
特殊元素的要求,再处理其他的元素.当直接求解困难时,可考虑用间接法求解,即先
不考虑限制条件,计算出排列总数,再减去不符合要求的排列数.
第六章 计数原理
“相邻”与“不相邻”问题
1.“捆绑法”解决相邻问题
解决相邻问题一般用“捆绑法”.将n个不同的元素排成一列,其中k(k≤n)个元素排
在相邻的位置上,求不同排法的种数的方法如下:(1)先将这k个元素“捆绑”在一
起,看成一个整体;(2)把这个整体当成一个元素与其他元素一起排列,有 种排
法;(3)“松绑”,即将“捆绑”在一起的元素进行内部排列,其排列方法有 种;(4)
由分步乘法计数原理知,符合条件的排法有 种.
第六章 计数原理
2.“插空法”解决不相邻问题
解决不相邻问题通常用“插空法”.将n个不同的元素排成一列,其中k 当n为奇数
时,k≤ ;当n为偶数时,k≤ 个元素互不相邻,求不同排法的种数的方法如下:
(1)将没有不相邻要求的(n-k)个元素排成一排,其排列方法有 种;(2)将要求两两
不相邻的k个元素插入(n-k+1)个空隙中,相当于从(n-k+1)个空隙中选出k个分别分配
给两两不相邻的k个元素,其排列方法有 种;(3)根据分步乘法计数原理知,符合
条件的排法有 种.
第六章 计数原理
“定序”问题
在排列问题中,某些元素在题意中已排定了顺序,对这些元素进行排列时,不再考虑
其顺序.在具体的计算过程中,可采用“除阶乘法”解决,即n个元素的全排列中有m
(m≤n)个元素的顺序固定,则满足题意的排法有 种.
第六章 计数原理
7名师生站成一排照相留念,其中老师1人,男学生4人,女学生2人.分别求满足下
列情况的不同站法的种数.
(1)老师甲必须站在中间或两端;
(2)2名女学生必须相邻而站;
(3)4名男学生互不相邻;
(4)若4名男学生身高都不等,按从高到低的顺序站.
第六章 计数原理
解析 (1)先考虑甲有 种站法,再考虑其余6人全排列,故不同站法的种数为
=2 160.
(2)2名女学生相邻而站有 种站法,视为一个整体并与其余5人全排列,有 种排
法,所以不同站法的种数为 =1 440.
(3)先站老师和女学生,有 种站法,再在老师和女学生站位的空(含两端)中插入男
学生,每空一人,则插入方法有 种,所以不同站法的种数为 =144.
(4)在7人全排列的所有站法中,4名男学生不考虑身高顺序的站法有 种,而从高到
低顺序站有从左到右和从右到左2种,所以不同站法的种数为2× =420.
第六章 计数原理
元宵节灯展后,如图悬挂的6盏不同的花灯需要取下,每次取1盏,共有 种不
同取法.(用数字作答)
第六章 计数原理
思路点拨
将问题转化为六个元素进行排列,而每一串的2盏花灯都有顺序,自下而上,所以是
排列中的“定序”问题.
解析 先将6盏花灯全排列共有 种排法,因为取花灯时每次只能取1盏,且每串花
灯必须先取下面的花灯,即每串2盏花灯取下的顺序确定,所以取下6盏不同的花灯,
每次取1盏,共有 = =90种不同取法.
答案 90
第六章 计数原理
3 |与数字有关的排列问题
数字排列问题的本质是“元素”占“位置”问题,有限制条件的排列问题的限制
条件主要表现在某元素不排在某个位置上或某个位置不排某些元素,解决该类排
列问题的主要方法是按照“优先”原则,即优先排特殊元素或优先满足特殊位置,
若一个位置安排的元素影响到另一个位置的元素个数时,应分类讨论.
含有数字“0”的排列问题中,有些隐含了数字“0”不能在首位的条件,应将其视
为有限制条件的元素优先进行排列.若在一个题目中,除了数字“0”以外还有其他
受限制的数字,则应考虑受限制的数字对位置的选择会不会影响数字“0”对位置
的选择,若有影响,则应分类讨论.
第六章 计数原理
从分别印有数字0,3,5,7,9的5张卡片中,任意抽出3张组成三位数.
(1)求可以组成多少个大于500的三位数;
(2)求可以组成多少个是5的倍数的三位数;
(3)若印有9的卡片,既可以当9用,也可以当6用,求可以组成多少个三位数.
思路点拨
(1)从首位大于或等于5进行分析.(2)从个位为0或5入手.(3)对特殊卡片9分被抽取和
未被抽取两种情况进行分析,当被抽取时又可以作为数字6用.
解析 (1)百位可以从5,7,9三张卡片中任取一张,十位和个位则可从剩下的卡片中
任取,所以可以组成大于500的三位数的个数为 =3×4×3=36.
(2)分两种情况:若个位为0,则十位和百位可从3,5,7,9中任取,有 =12个;若个位为5,
则百位只能从3,7,9中任取一张,十位再从剩下的3张卡片中任取一张,所以有 =
9个.
第六章 计数原理
所以可以组成12+9=21个是5的倍数的三位数.
(3)分三种情况:若卡片9没有被抽取,则这样的三位数有 =18个;若卡片9被抽取,
且0未被抽取,则这样的三位数有3 ×2=36个;若卡片9被抽取,且0被抽取,则这样的
三位数有2×3×2 =24个.
所以这样的三位数共有18+36+24=78个.
第六章 计数原理
用0,1,2,3,4,5这六个数字可以组成多少个:
(1)无重复数字且个位数字不是5的六位数
(2)无重复数字且比1 325大的四位数
(3)无重复数字的六位数 若这些六位数按从小到大的顺序排成一列,则240 135是该
列数的第几项
解析 (1)解法一:间接法.
0在十万位的六位数或5在个位的六位数都有 个,0在十万位且5在个位的六位数
有 个.
故符合题意的六位数共有 -2 + =504个.
第六章 计数原理
解法二:直接法.
十万位数字的排法因个位上数字为0与不为0而有所不同,因此需分两类:
第一类:当个位数字为0时,符合题意的六位数有 个;
第二类:当个位数字不为0时,符合题意的六位数有 个.
故符合题意的六位数共有 + =504个.
(2)符合题意的四位数可分为三类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共4 个;
第二类:形如14□□,15□□,共有2 个;
第三类:形如134□,135□,共有2 个.
由分类加法计数原理知,无重复数字且比1 325大的四位数共有4 +2 +2 =270个.
(3)符合题意的六位数共有 - =600个.由于是六位数,故十万位不能为0,则十万位
为1的有 个,十万位为2,万位上为0或1或3的共有3 个,∵ +3 +1=193,∴240 1
35是该列数的第193项.
第六章 计数原理
