6.3.2二项式系数的性质 课件(共10张PPT)
文档属性
| 名称 | 6.3.2二项式系数的性质 课件(共10张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 20:54:00 | ||
图片预览




文档简介
(共10张PPT)
6.3.2 二项式系数的性质
1.掌握二项式系数的性质及其简单应用.
2.建立杨辉三角与二项式系数之间的联系,并探索其中的规律.
第六章 计数原理
1 |二项式系数的性质
1.对称性
与首末两端“① 等距离 ”的两个二项式系数相等,即 = .
2.增减性与最大值
当k< 时, ② 随k的增加而增大 ;当k> 时, 随k的增加而减小.当n是偶
数时,中间的一项③ 取得最大值;当n是奇数时,中间的两项④ 与
相等,且同时取得最大值.
3.各二项式系数的和
(a+b)n的展开式的各二项式系数的和等于2n,即⑤ + + +…+ =2n .
(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.即⑥
+ + +… =⑦ + + +… .
第六章 计数原理
1.二项展开式的各二项式系数的和为 + +…+ . ( )
二项展开式的各二项式系数的和为 + + +…+ =2n.
2.二项展开式中系数最大项与二项式系数最大项相同. ( )
3.若(a+b)n的展开式的第4项的二项式系数与第6项的二项式系数相等,则第5项一定
是二项式系数最大项. ( √ )
由题意可知, = ,所以n=3+5=8,(a+b)8的展开式的中间项为第5项,所以第5项为二
项式系数最大项.
4.(x+2)5与(x-2)5的展开式的各二项式系数和一定不相等.( )
(x+2)5与(x-2)5展开式的各二项式系数和均为25.
判断正误,正确的画“ √” ,错误的画“ ” .
第六章 计数原理
1 |二项式系数的性质及其应用
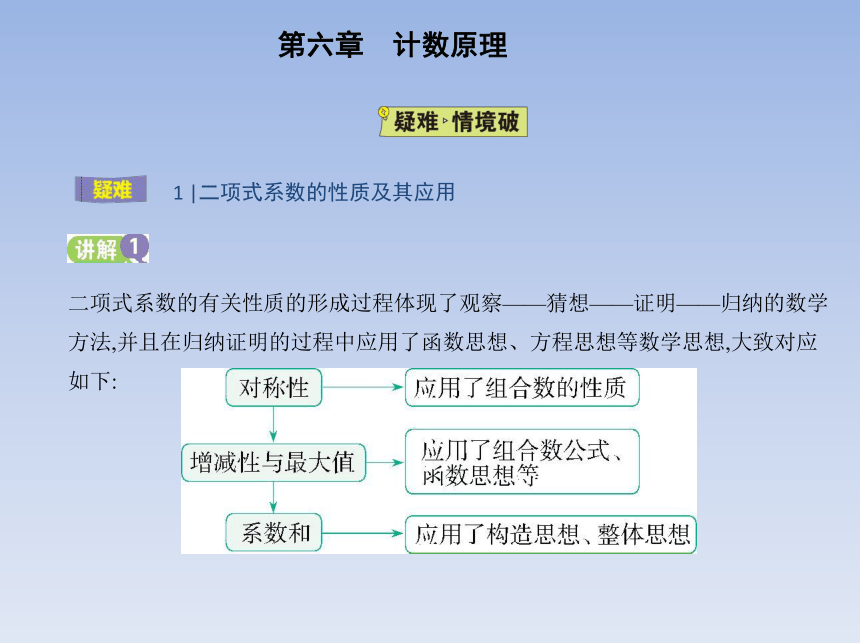
二项式系数的有关性质的形成过程体现了观察——猜想——证明——归纳的数学
方法,并且在归纳证明的过程中应用了函数思想、方程思想等数学思想,大致对应
如下:
第六章 计数原理
求二项式系数最大的项,可根据二项式系数的性质,当n为奇数时,中间两项的二项
式系数最大;当n为偶数时,中间一项的二项式系数最大.
求二项展开式中系数的最值问题有两种思路:思路一,二项展开式中的系数是关于
正整数n的式子,可以看成关于n的函数,利用判断函数单调性的方法判断系数的增
减性,从而求出系数的最值;思路二,在系数均为正值的前提下,求它们的最大值只需
比较相邻两个系数的大小,根据其展开式的通项正确地列出不等式(组)即可.
根据二项式系数的性质求参数的关键是正确列出与参数有关的关系式,然后解此
关系式即可.必要时,需检验所求参数是否符合题目要求.
第六章 计数原理
在(3x-2y)20的展开式中,求:
(1)二项式系数最大的项;
(2)系数绝对值最大的项;
(3)系数最大的项.
解析 (1)二项式系数最大的项是第11项,T11= ×310×(-2)10x10y10= ×610x10y10.
(2)设系数绝对值最大的项是第r+1(0≤r≤20,r∈N)项,
于是
化简得
解得 ≤r≤ (r∈N),所以r=8,
即T9= ×312×28x12y8是系数绝对值最大的项.
第六章 计数原理
(3)由于系数为正的项为y的偶次方项,因此可设第2k-1(1≤k≤11,k∈N)项系数最大,
于是
所以
解得k=5,即第2×5-1=9项系数最大,T9= ×312×28×x12y8.
方法总结 求二项式系数最大的项,利用性质知展开式的中间项(或中间两项)是二
项式系数最大的项.求展开式中系数最大的项,当展开式中有些项的系数是负数,有
些项的系数是正数时,只能在系数为正数的这些项中找,只需比较系数为正数的相
邻的两项,列出不等式(组),解出此时对应的“r”即可.
第六章 计数原理
2 |杨辉三角问题
解决与杨辉三角有关的问题的一般思路
第六章 计数原理
如图为杨辉三角,如果去掉杨辉三角中的所有为1的项,依次构成2,3,3,4,6,4,5,10,10,
5,6,…,则此数列的前50项和为 ( )
A.2 025 B.3 052 C.3 053 D.3 049
第六章 计数原理
解析 去除所有为1的项后,由题图可知前n行共有 个数,
当n=10时, =55,即前10行共有55个数.
因为第n-1行的各数之和为 + +…+ =2n-2,
所以前10行的各数之和为(22-2)+(23-2)+…+(211-2)=212-24=4 072.
因为第10行最后5个数从右至左依次为 , , , , ,
所以此数列的前50项的和为4 072- - - - - =4 072-11-55-165-330-462=3 0
49.
答案 D
第六章 计数原理
6.3.2 二项式系数的性质
1.掌握二项式系数的性质及其简单应用.
2.建立杨辉三角与二项式系数之间的联系,并探索其中的规律.
第六章 计数原理
1 |二项式系数的性质
1.对称性
与首末两端“① 等距离 ”的两个二项式系数相等,即 = .
2.增减性与最大值
当k< 时, ② 随k的增加而增大 ;当k> 时, 随k的增加而减小.当n是偶
数时,中间的一项③ 取得最大值;当n是奇数时,中间的两项④ 与
相等,且同时取得最大值.
3.各二项式系数的和
(a+b)n的展开式的各二项式系数的和等于2n,即⑤ + + +…+ =2n .
(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.即⑥
+ + +… =⑦ + + +… .
第六章 计数原理
1.二项展开式的各二项式系数的和为 + +…+ . ( )
二项展开式的各二项式系数的和为 + + +…+ =2n.
2.二项展开式中系数最大项与二项式系数最大项相同. ( )
3.若(a+b)n的展开式的第4项的二项式系数与第6项的二项式系数相等,则第5项一定
是二项式系数最大项. ( √ )
由题意可知, = ,所以n=3+5=8,(a+b)8的展开式的中间项为第5项,所以第5项为二
项式系数最大项.
4.(x+2)5与(x-2)5的展开式的各二项式系数和一定不相等.( )
(x+2)5与(x-2)5展开式的各二项式系数和均为25.
判断正误,正确的画“ √” ,错误的画“ ” .
第六章 计数原理
1 |二项式系数的性质及其应用
二项式系数的有关性质的形成过程体现了观察——猜想——证明——归纳的数学
方法,并且在归纳证明的过程中应用了函数思想、方程思想等数学思想,大致对应
如下:
第六章 计数原理
求二项式系数最大的项,可根据二项式系数的性质,当n为奇数时,中间两项的二项
式系数最大;当n为偶数时,中间一项的二项式系数最大.
求二项展开式中系数的最值问题有两种思路:思路一,二项展开式中的系数是关于
正整数n的式子,可以看成关于n的函数,利用判断函数单调性的方法判断系数的增
减性,从而求出系数的最值;思路二,在系数均为正值的前提下,求它们的最大值只需
比较相邻两个系数的大小,根据其展开式的通项正确地列出不等式(组)即可.
根据二项式系数的性质求参数的关键是正确列出与参数有关的关系式,然后解此
关系式即可.必要时,需检验所求参数是否符合题目要求.
第六章 计数原理
在(3x-2y)20的展开式中,求:
(1)二项式系数最大的项;
(2)系数绝对值最大的项;
(3)系数最大的项.
解析 (1)二项式系数最大的项是第11项,T11= ×310×(-2)10x10y10= ×610x10y10.
(2)设系数绝对值最大的项是第r+1(0≤r≤20,r∈N)项,
于是
化简得
解得 ≤r≤ (r∈N),所以r=8,
即T9= ×312×28x12y8是系数绝对值最大的项.
第六章 计数原理
(3)由于系数为正的项为y的偶次方项,因此可设第2k-1(1≤k≤11,k∈N)项系数最大,
于是
所以
解得k=5,即第2×5-1=9项系数最大,T9= ×312×28×x12y8.
方法总结 求二项式系数最大的项,利用性质知展开式的中间项(或中间两项)是二
项式系数最大的项.求展开式中系数最大的项,当展开式中有些项的系数是负数,有
些项的系数是正数时,只能在系数为正数的这些项中找,只需比较系数为正数的相
邻的两项,列出不等式(组),解出此时对应的“r”即可.
第六章 计数原理
2 |杨辉三角问题
解决与杨辉三角有关的问题的一般思路
第六章 计数原理
如图为杨辉三角,如果去掉杨辉三角中的所有为1的项,依次构成2,3,3,4,6,4,5,10,10,
5,6,…,则此数列的前50项和为 ( )
A.2 025 B.3 052 C.3 053 D.3 049
第六章 计数原理
解析 去除所有为1的项后,由题图可知前n行共有 个数,
当n=10时, =55,即前10行共有55个数.
因为第n-1行的各数之和为 + +…+ =2n-2,
所以前10行的各数之和为(22-2)+(23-2)+…+(211-2)=212-24=4 072.
因为第10行最后5个数从右至左依次为 , , , , ,
所以此数列的前50项的和为4 072- - - - - =4 072-11-55-165-330-462=3 0
49.
答案 D
第六章 计数原理
