8.1.1变量的相关关系8.1.2样本相关系数课件(共14张PPT)
文档属性
| 名称 | 8.1.1变量的相关关系8.1.2样本相关系数课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 21:09:13 | ||
图片预览






文档简介
(共14张PPT)
8.1 成对数据的统计相关性
8.1.1 变量的相关关系
8.1.2 样本相关系数
1.结合实例,了解样本相关系数的统计含义,了解样本相关系数与标准化数据向量
夹角的关系.
2.结合实例,会通过样本相关系数比较多组成对数据的相关性.
第八章 成对数据的统计分析
1 |变量的相关关系
1.相关关系
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这
种关系称为相关关系.
2.散点图
将成对样本数据用① 直角坐标系中的点 表示出来,由这些点组成的统计图就
叫做散点图.
第八章 成对数据的统计分析
3.正相关与负相关
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现② 增加 的趋
势,就称这两个变量正相关;当一个变量的值增加时,另一个变量的相应值呈现③
减少 的趋势,就称这两个变量负相关.
4.线性相关
一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在④ 一条直线
附近,则称这两个变量线性相关.
第八章 成对数据的统计分析
2 |样本相关系数
1.样本相关系数
r= r为变量x和变量y的样本相关系数.
2.样本相关系数r的特征
(1)r∈⑤ [-1,1] .
(2)当r>0时,称成对样本数据⑥ 正 相关;当r<0时,称成对样本数据⑦ 负 相关.
(3)当|r|越接近1时,成对样本数据的线性相关程度⑧ 越强 ;当|r|越接近0时,成对
样本数据的线性相关程度⑨ 越弱 .
第八章 成对数据的统计分析
1.相关关系是一种非确定性关系. ( √ )
2.当r=0时,成对数据间没有任何关系. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
当r=0时,只表明成对数据间没有线性相关关系,但不排除它们之间有其他关系.
3.若r1=-0.95,r2=0.85,则体现两变量相关关系较强的是r2. ( )
当|r|越接近1时,成对数据的线性相关程度越强,所以体现两变量相关关系较强的是r
1.
4.当变量x的取值为3,4,5,6,7时,变量y对应的值依次为4.0,2.5,-0.5,-1,-2,则可知变量x
和y是负相关. ( √ )
第八章 成对数据的统计分析
1 |两个变量相关性的判断
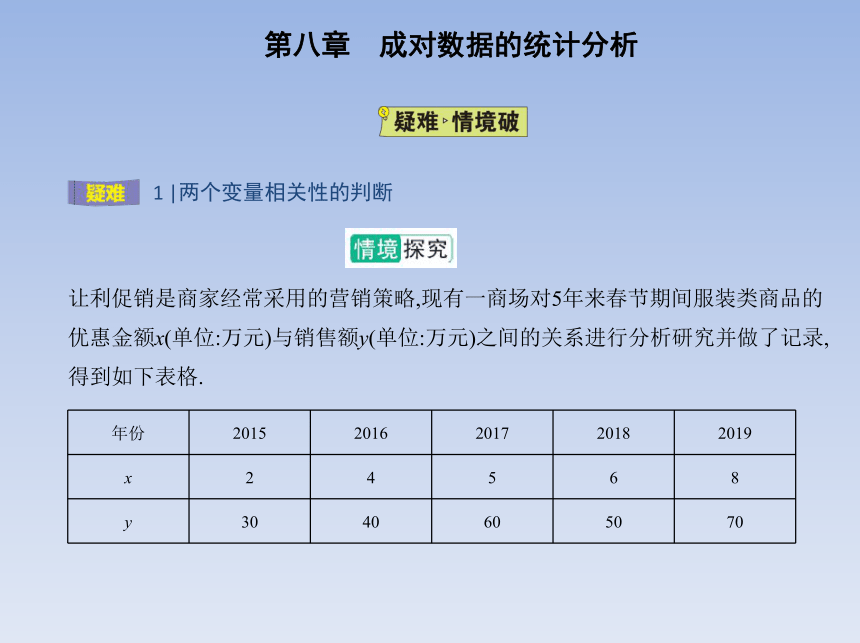
让利促销是商家经常采用的营销策略,现有一商场对5年来春节期间服装类商品的
优惠金额x(单位:万元)与销售额y(单位:万元)之间的关系进行分析研究并做了记录,
得到如下表格.
年份 2015 2016 2017 2018 2019
x 2 4 5 6 8
y 30 40 60 50 70
第八章 成对数据的统计分析
1.请你根据题目所给数据画出相应的散点图,并判断服装类商品的优惠金额与销售
额是否线性相关,如果是线性相关,那么是正相关还是负相关
提示:散点图如图所示.由图可知,各散点基本在一条直线附近,所以可以认为服装类
商品的优惠金额与销售额是线性相关的,且是正相关.
第八章 成对数据的统计分析
2.计算x与y的样本相关系数,并依据样本相关系数判断服装类商品的优惠金额与销
售额的线性相关程度是强还是弱.
提示:r= ≈0.919,所以可以认为服装类商品的优惠金额与销售额
的线性相关程度较强.
第八章 成对数据的统计分析
利用散点图判断两个变量的相关性
(1)一般地,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第
一、第三象限,对应的成对数据同号的居多;如果变量x和y负相关,那么关于均值平
移后的大多数散点将分布在第二、第四象限,对应的成对数据异号的居多.
(2)如果散点落在一条直线附近,则认为这两个变量线性相关.
利用样本相关系数判断两个变量相关性强弱
样本相关系数r是从数值上来判断变量间的线性相关程度,是定量分析法.|r|刻画了
样本点集中于某条直线的程度.
|r|越接近1,散点图中的样本点分布越接近一条直线,两个变量的线性相关程度越强.
第八章 成对数据的统计分析
(2020广东东莞高三期末调研测试)某农科所对冬季昼夜温差(最高温度与最低温度
的差)大小与某反季节大豆新品种一天内发芽数之间的关系进行了分析研究,他们
分别记录了12月1日至12月6日每天昼夜最高、最低的温度(如图甲),以及实验室每
天每100颗种子中的发芽数情况(如图乙).
图甲
第八章 成对数据的统计分析
图乙
(1)请画出发芽数y与温差x的散点图;
(2)判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度.
参考数据:
第八章 成对数据的统计分析
参考公式:样本相关系数r=
(当|r|>0.75时,认为成对样本数据的线性相关程度较强).
解析 (1)散点图如图所示.
第八章 成对数据的统计分析
(2)r=
≈ ≈0.952.
由样本相关系数r≈0.952>0.75,可以推断发芽数与温差这两个变量正相关,且线性
相关程度较强.
规律总结 判断两个变量之间的线性相关关系一般用散点图,但在作图中,由于存
在误差,有时很难判断这些点是否分布在一条直线附近,此时可以利用样本相关系
数r来判断.样本相关系数是从数值上来判断的,是定量分析法,比散点图(定性分析
法)要精细得多.
第八章 成对数据的统计分析
2 |样本相关系数的应用
样本相关系数是对两个变量相关程度进行定量刻画,|r|越大,表明两个变量之
间的线性相关程度越强,运用样本相关系数进行判断的一般步骤如下:
(1)整理数据,求出相关值;(2)计算样本相关系数;(3)得出结论.
第八章 成对数据的统计分析
8.1 成对数据的统计相关性
8.1.1 变量的相关关系
8.1.2 样本相关系数
1.结合实例,了解样本相关系数的统计含义,了解样本相关系数与标准化数据向量
夹角的关系.
2.结合实例,会通过样本相关系数比较多组成对数据的相关性.
第八章 成对数据的统计分析
1 |变量的相关关系
1.相关关系
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这
种关系称为相关关系.
2.散点图
将成对样本数据用① 直角坐标系中的点 表示出来,由这些点组成的统计图就
叫做散点图.
第八章 成对数据的统计分析
3.正相关与负相关
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现② 增加 的趋
势,就称这两个变量正相关;当一个变量的值增加时,另一个变量的相应值呈现③
减少 的趋势,就称这两个变量负相关.
4.线性相关
一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在④ 一条直线
附近,则称这两个变量线性相关.
第八章 成对数据的统计分析
2 |样本相关系数
1.样本相关系数
r= r为变量x和变量y的样本相关系数.
2.样本相关系数r的特征
(1)r∈⑤ [-1,1] .
(2)当r>0时,称成对样本数据⑥ 正 相关;当r<0时,称成对样本数据⑦ 负 相关.
(3)当|r|越接近1时,成对样本数据的线性相关程度⑧ 越强 ;当|r|越接近0时,成对
样本数据的线性相关程度⑨ 越弱 .
第八章 成对数据的统计分析
1.相关关系是一种非确定性关系. ( √ )
2.当r=0时,成对数据间没有任何关系. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
当r=0时,只表明成对数据间没有线性相关关系,但不排除它们之间有其他关系.
3.若r1=-0.95,r2=0.85,则体现两变量相关关系较强的是r2. ( )
当|r|越接近1时,成对数据的线性相关程度越强,所以体现两变量相关关系较强的是r
1.
4.当变量x的取值为3,4,5,6,7时,变量y对应的值依次为4.0,2.5,-0.5,-1,-2,则可知变量x
和y是负相关. ( √ )
第八章 成对数据的统计分析
1 |两个变量相关性的判断
让利促销是商家经常采用的营销策略,现有一商场对5年来春节期间服装类商品的
优惠金额x(单位:万元)与销售额y(单位:万元)之间的关系进行分析研究并做了记录,
得到如下表格.
年份 2015 2016 2017 2018 2019
x 2 4 5 6 8
y 30 40 60 50 70
第八章 成对数据的统计分析
1.请你根据题目所给数据画出相应的散点图,并判断服装类商品的优惠金额与销售
额是否线性相关,如果是线性相关,那么是正相关还是负相关
提示:散点图如图所示.由图可知,各散点基本在一条直线附近,所以可以认为服装类
商品的优惠金额与销售额是线性相关的,且是正相关.
第八章 成对数据的统计分析
2.计算x与y的样本相关系数,并依据样本相关系数判断服装类商品的优惠金额与销
售额的线性相关程度是强还是弱.
提示:r= ≈0.919,所以可以认为服装类商品的优惠金额与销售额
的线性相关程度较强.
第八章 成对数据的统计分析
利用散点图判断两个变量的相关性
(1)一般地,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第
一、第三象限,对应的成对数据同号的居多;如果变量x和y负相关,那么关于均值平
移后的大多数散点将分布在第二、第四象限,对应的成对数据异号的居多.
(2)如果散点落在一条直线附近,则认为这两个变量线性相关.
利用样本相关系数判断两个变量相关性强弱
样本相关系数r是从数值上来判断变量间的线性相关程度,是定量分析法.|r|刻画了
样本点集中于某条直线的程度.
|r|越接近1,散点图中的样本点分布越接近一条直线,两个变量的线性相关程度越强.
第八章 成对数据的统计分析
(2020广东东莞高三期末调研测试)某农科所对冬季昼夜温差(最高温度与最低温度
的差)大小与某反季节大豆新品种一天内发芽数之间的关系进行了分析研究,他们
分别记录了12月1日至12月6日每天昼夜最高、最低的温度(如图甲),以及实验室每
天每100颗种子中的发芽数情况(如图乙).
图甲
第八章 成对数据的统计分析
图乙
(1)请画出发芽数y与温差x的散点图;
(2)判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度.
参考数据:
第八章 成对数据的统计分析
参考公式:样本相关系数r=
(当|r|>0.75时,认为成对样本数据的线性相关程度较强).
解析 (1)散点图如图所示.
第八章 成对数据的统计分析
(2)r=
≈ ≈0.952.
由样本相关系数r≈0.952>0.75,可以推断发芽数与温差这两个变量正相关,且线性
相关程度较强.
规律总结 判断两个变量之间的线性相关关系一般用散点图,但在作图中,由于存
在误差,有时很难判断这些点是否分布在一条直线附近,此时可以利用样本相关系
数r来判断.样本相关系数是从数值上来判断的,是定量分析法,比散点图(定性分析
法)要精细得多.
第八章 成对数据的统计分析
2 |样本相关系数的应用
样本相关系数是对两个变量相关程度进行定量刻画,|r|越大,表明两个变量之
间的线性相关程度越强,运用样本相关系数进行判断的一般步骤如下:
(1)整理数据,求出相关值;(2)计算样本相关系数;(3)得出结论.
第八章 成对数据的统计分析
