8.2.1一元线性回归模型8.2.2 一元线性回归模型参数的最小二乘估计(共15张PPT)
文档属性
| 名称 | 8.2.1一元线性回归模型8.2.2 一元线性回归模型参数的最小二乘估计(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 21:31:30 | ||
图片预览






文档简介
(共15张PPT)
8.2 一元线性回归模型及其应用
8.2.1 一元线性回归模型
8.2.2 一元线性回归模型参数的最小二乘估计
1.结合具体实例,了解一元线性回归模型的含义,了解模型参数的统计意义.
2.了解最小二乘法原理,掌握一元线性回归模型参数的最小二乘估计方法,会使用
相关的统计软件.
3.针对实际问题,会用一元线性回归模型进行预测.
第八章 成对数据的统计分析
第八章 成对数据的统计分析
1 |一元线性回归模型
把式子① 称为Y关于x的一元线性回归模型.其中,Y称为
因变量或② 响应变量 ,x称为自变量或③ 解释变量 ;a和b为模型的未知参
数,a称为截距参数,b称为④ 斜率参数 ;e是Y与bx+a之间的随机误差.如果e=0,那
么Y与x之间的关系就可用一元线性函数模型来描述.
2 |线性回归方程与最小二乘法
设满足一元线性回归模型的两个变量的n对样本数据为(x1,y1),(x2,y2),…,(xn,yn),
由yi=bxi+a+ei(i=1,2,…,n),得|yi-(bxi+a)|=|ei|,显然|ei|越小,表示样本数据点离直线y=bx+
a的竖直距离越小.
通常用各散点到直线的竖直距离的平方之和Q= 来刻画各样本观测数据
与直线y=bx+a的“整体接近程度”.
当a,b的取值为 时,Q达到最小.将⑦ = x+ 称为Y关于x的
经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线.这种
求经验回归方程的方法叫做最小二乘法,求得的 , 叫做b,a的最小二乘估计.
经验回归直线一定过点( , ).
第八章 成对数据的统计分析
3 |残差分析
对于响应变量Y,通过观测得到的数据称为观测值,通过⑧ 经验回归方程 得到的
称为预测值,观测值减去预测值称为⑨ 残差 .残差是随机误差的估计结果,通
过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可
疑数据等,这方面工作称为残差分析.
第八章 成对数据的统计分析
4 |刻画回归效果的方式
1.残差图法
作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样
作出的图形称为残差图.在残差图中,残差点比较均匀地落在以横轴为对称轴的水
平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,说明模型
拟合精度越高.
2.残差平方和法
残差平方和为 (yi- )2,残差平方和⑩ 越小 ,模型拟合效果越好.
3.利用R2刻画拟合效果
R2=1- .
R2越大,模型的拟合效果越 好 ,R2越小,模型的拟合效果越 差 .
第八章 成对数据的统计分析
1.求经验回归方程前可以不进行相关性检验. ( )
2.在残差图中,纵坐标为残差,横坐标可以选为样本编号. ( √ )
3.利用经验回归方程求出的值是准确值. ( )
4.对于散点图中的点没有均匀分布在某条直线附近或毫无规则可言的两个变量,用
最小二乘法求不出对应的回归直线. ( )
5.y的实际值与估计值之间的误差记为e,称之为随机误差,它主要是由计算产生的误
差,没有其他原因.( )
6.用R2来刻画模型的拟合效果时,R2大于1对应模型的拟合效果比R2小于1对应模型
的拟合效果好. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
第八章 成对数据的统计分析
1 |如何检验回归模型的拟合效果
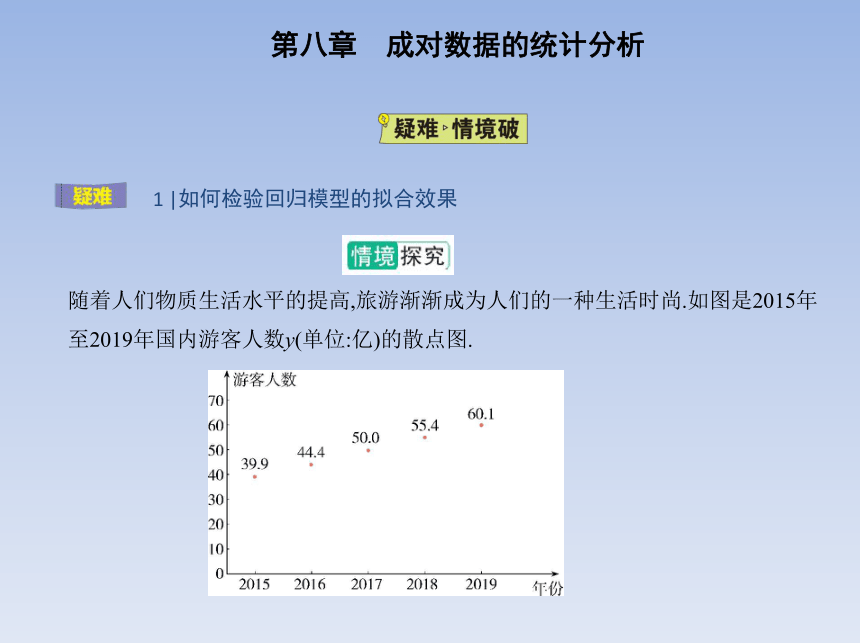
随着人们物质生活水平的提高,旅游渐渐成为人们的一种生活时尚.如图是2015年
至2019年国内游客人数y(单位:亿)的散点图.
第八章 成对数据的统计分析
1.根据2015年至2019年的数据建立了游客人数y与时间编号t(2015年至2019年时间
编号t的值依次记为1,2,…,5)的3个回归模型:① =36.17e0.104 1t;② =5.14t+34.54;③
=12.412ln t+38.076.你认为用哪个模型能更好地刻画y与t之间的关系
提示:观察散点图,散点的分布更接近一条直线,故选择回归模型②.
2.根据问题1中你选定的经验回归方程,作出残差图,并作出分析.
提示:依据经验回归方程 =5.14t+34.54,得残差数据如表所示.
t 1 2 3 4 5
残差 0.22 -0.42 0.04 0.3 -0.14
第八章 成对数据的统计分析
以时间编号为横坐标,残差为纵坐标作出残差图如图所示.由图可知,残差点分布较
均匀,即用上述回归模型拟合数据效果好.
3.根据问题1中你选定的经验回归方程,计算R2,并作相关说明.
提示:利用R2的计算公式得R2≈0.998 7,因为R2越大,模型的拟合效果越好,所以从R2
分析,该模型拟合数据效果好.
第八章 成对数据的统计分析
检验回归模型的拟合效果一般有两种方法:
1.残差分析
通过残差分析发现原始数据中的可疑数据,判断所建立模型的拟合效果.其步骤是:
计算残差、画残差图、在残差图中分析残差特性.
2.利用R2分析
通过公式R2=1- 计算R2,其中 表示残差平方和. R2越大,残差平方和
越小,模型的拟合效果越好;R2越小,残差平方和越大,模型的拟合效果越差.
第八章 成对数据的统计分析
2 |经验回归方程的求解与应用
(1)确定研究对象,明确哪个变量是解释变量,哪个变量是响应变量.
(2)画出解释变量和响应变量的散点图,观察它们之间的关系(如是否存在线性关系
等).
(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性经验回
归方程).
(4)按一定规则(如最小二乘法)估计经验回归方程中的参数.
(5)对变量值的预测,即解释变量取某值时,对响应变量的值进行预测.
第八章 成对数据的统计分析
(2020全国百所名校新高考模拟示范卷)从中国教育在线官方公布的考研动机调查
来看,本科生扎堆考研的原因大概集中在这6个方面:本科就业压力大,提升竞争力;
通过考研选择真正感兴趣的专业;为了获得学历;继续深造;随大流;有名校情结.如
图是2015~2019年全国硕士研究生报考人数的折线图.
第八章 成对数据的统计分析
(1)求y关于t的经验回归方程;
(2)根据(1)中的经验回归方程,预测2021年全国硕士研究生报考人数.
参考数据: (ti- )(yi- )=311.
经验回归方程 = t+ 中,
= .
第八章 成对数据的统计分析
解析 (1)由题中数据得
= =3,
= =214.2,
=(-2)2+(-1)2+02+12+22=10,
由参考数据知,
=311,
第八章 成对数据的统计分析
所以 = = =31.1,
= - =214.2-31.1×3=120.9,
故所求经验回归方程为 =31.1t+120.9.
(2)将2021年对应的t=7代入经验回归方程,得
=31.1×7+120.9=338.6,
所以预测2021年全国硕士研究生报考人数为338.6万.
第八章 成对数据的统计分析
8.2 一元线性回归模型及其应用
8.2.1 一元线性回归模型
8.2.2 一元线性回归模型参数的最小二乘估计
1.结合具体实例,了解一元线性回归模型的含义,了解模型参数的统计意义.
2.了解最小二乘法原理,掌握一元线性回归模型参数的最小二乘估计方法,会使用
相关的统计软件.
3.针对实际问题,会用一元线性回归模型进行预测.
第八章 成对数据的统计分析
第八章 成对数据的统计分析
1 |一元线性回归模型
把式子① 称为Y关于x的一元线性回归模型.其中,Y称为
因变量或② 响应变量 ,x称为自变量或③ 解释变量 ;a和b为模型的未知参
数,a称为截距参数,b称为④ 斜率参数 ;e是Y与bx+a之间的随机误差.如果e=0,那
么Y与x之间的关系就可用一元线性函数模型来描述.
2 |线性回归方程与最小二乘法
设满足一元线性回归模型的两个变量的n对样本数据为(x1,y1),(x2,y2),…,(xn,yn),
由yi=bxi+a+ei(i=1,2,…,n),得|yi-(bxi+a)|=|ei|,显然|ei|越小,表示样本数据点离直线y=bx+
a的竖直距离越小.
通常用各散点到直线的竖直距离的平方之和Q= 来刻画各样本观测数据
与直线y=bx+a的“整体接近程度”.
当a,b的取值为 时,Q达到最小.将⑦ = x+ 称为Y关于x的
经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线.这种
求经验回归方程的方法叫做最小二乘法,求得的 , 叫做b,a的最小二乘估计.
经验回归直线一定过点( , ).
第八章 成对数据的统计分析
3 |残差分析
对于响应变量Y,通过观测得到的数据称为观测值,通过⑧ 经验回归方程 得到的
称为预测值,观测值减去预测值称为⑨ 残差 .残差是随机误差的估计结果,通
过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可
疑数据等,这方面工作称为残差分析.
第八章 成对数据的统计分析
4 |刻画回归效果的方式
1.残差图法
作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样
作出的图形称为残差图.在残差图中,残差点比较均匀地落在以横轴为对称轴的水
平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,说明模型
拟合精度越高.
2.残差平方和法
残差平方和为 (yi- )2,残差平方和⑩ 越小 ,模型拟合效果越好.
3.利用R2刻画拟合效果
R2=1- .
R2越大,模型的拟合效果越 好 ,R2越小,模型的拟合效果越 差 .
第八章 成对数据的统计分析
1.求经验回归方程前可以不进行相关性检验. ( )
2.在残差图中,纵坐标为残差,横坐标可以选为样本编号. ( √ )
3.利用经验回归方程求出的值是准确值. ( )
4.对于散点图中的点没有均匀分布在某条直线附近或毫无规则可言的两个变量,用
最小二乘法求不出对应的回归直线. ( )
5.y的实际值与估计值之间的误差记为e,称之为随机误差,它主要是由计算产生的误
差,没有其他原因.( )
6.用R2来刻画模型的拟合效果时,R2大于1对应模型的拟合效果比R2小于1对应模型
的拟合效果好. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
第八章 成对数据的统计分析
1 |如何检验回归模型的拟合效果
随着人们物质生活水平的提高,旅游渐渐成为人们的一种生活时尚.如图是2015年
至2019年国内游客人数y(单位:亿)的散点图.
第八章 成对数据的统计分析
1.根据2015年至2019年的数据建立了游客人数y与时间编号t(2015年至2019年时间
编号t的值依次记为1,2,…,5)的3个回归模型:① =36.17e0.104 1t;② =5.14t+34.54;③
=12.412ln t+38.076.你认为用哪个模型能更好地刻画y与t之间的关系
提示:观察散点图,散点的分布更接近一条直线,故选择回归模型②.
2.根据问题1中你选定的经验回归方程,作出残差图,并作出分析.
提示:依据经验回归方程 =5.14t+34.54,得残差数据如表所示.
t 1 2 3 4 5
残差 0.22 -0.42 0.04 0.3 -0.14
第八章 成对数据的统计分析
以时间编号为横坐标,残差为纵坐标作出残差图如图所示.由图可知,残差点分布较
均匀,即用上述回归模型拟合数据效果好.
3.根据问题1中你选定的经验回归方程,计算R2,并作相关说明.
提示:利用R2的计算公式得R2≈0.998 7,因为R2越大,模型的拟合效果越好,所以从R2
分析,该模型拟合数据效果好.
第八章 成对数据的统计分析
检验回归模型的拟合效果一般有两种方法:
1.残差分析
通过残差分析发现原始数据中的可疑数据,判断所建立模型的拟合效果.其步骤是:
计算残差、画残差图、在残差图中分析残差特性.
2.利用R2分析
通过公式R2=1- 计算R2,其中 表示残差平方和. R2越大,残差平方和
越小,模型的拟合效果越好;R2越小,残差平方和越大,模型的拟合效果越差.
第八章 成对数据的统计分析
2 |经验回归方程的求解与应用
(1)确定研究对象,明确哪个变量是解释变量,哪个变量是响应变量.
(2)画出解释变量和响应变量的散点图,观察它们之间的关系(如是否存在线性关系
等).
(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性经验回
归方程).
(4)按一定规则(如最小二乘法)估计经验回归方程中的参数.
(5)对变量值的预测,即解释变量取某值时,对响应变量的值进行预测.
第八章 成对数据的统计分析
(2020全国百所名校新高考模拟示范卷)从中国教育在线官方公布的考研动机调查
来看,本科生扎堆考研的原因大概集中在这6个方面:本科就业压力大,提升竞争力;
通过考研选择真正感兴趣的专业;为了获得学历;继续深造;随大流;有名校情结.如
图是2015~2019年全国硕士研究生报考人数的折线图.
第八章 成对数据的统计分析
(1)求y关于t的经验回归方程;
(2)根据(1)中的经验回归方程,预测2021年全国硕士研究生报考人数.
参考数据: (ti- )(yi- )=311.
经验回归方程 = t+ 中,
= .
第八章 成对数据的统计分析
解析 (1)由题中数据得
= =3,
= =214.2,
=(-2)2+(-1)2+02+12+22=10,
由参考数据知,
=311,
第八章 成对数据的统计分析
所以 = = =31.1,
= - =214.2-31.1×3=120.9,
故所求经验回归方程为 =31.1t+120.9.
(2)将2021年对应的t=7代入经验回归方程,得
=31.1×7+120.9=338.6,
所以预测2021年全国硕士研究生报考人数为338.6万.
第八章 成对数据的统计分析
