第八章 成对数据的统计分析 8.1~8.3 综合拔高练(Word含答案解析)
文档属性
| 名称 | 第八章 成对数据的统计分析 8.1~8.3 综合拔高练(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 116.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 21:39:31 | ||
图片预览




文档简介
8.1~8.3 综合拔高练
五年高考练
考点1 变量的相关关系与线性回归模型
1.(2020课标全国Ⅰ理,5,5分,)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
2.(2020课标全国Ⅱ理,18,12分,)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得xi=60,yi=1 200,(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
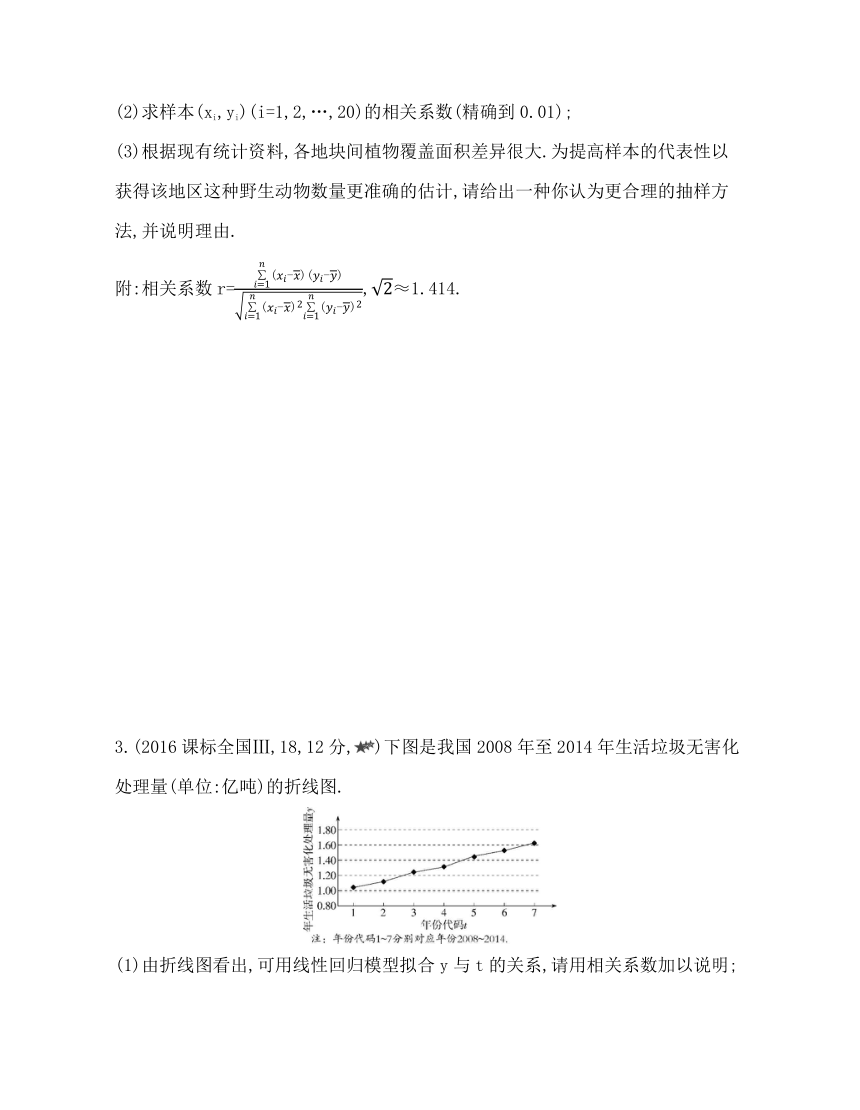
3.(2016课标全国Ⅲ,18,12分,)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:yi=9.32,tiyi=40.17,=0.55,≈2.646.
参考公式:相关系数r=,
回归方程=+t中斜率和截距最小二乘估计公式分别为:=,=-.
考点2 独立性检验及其应用
4.(2020新高考Ⅰ,19,12分,)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和SO2浓度(单位:μg/m3),得下表:
SO2 PM2.5 [0,50] (50,150] (150,475]
[0,35] 32 18 4
(35,75] 6 8 12
(75,115] 3 7 10
(1)估计事件“该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150”的概率;
(2)根据所给数据,完成下面的2×2列联表:
SO2 PM2.5 [0,150] (150,475]
[0,75]
(75,115]
(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
附:K2=,
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
.
5.(2020课标全国Ⅲ理,18,12分,)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 [0,200] (200,400] (400,600]
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
人次≤400 人次>400
空气质量好
空气质量不好
附:K2=,
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
.
三年模拟练
应用实践
1.(2020陕西西安八校联考,)设两个变量x和y之间线性相关,它们的样本相关系数为r,y关于x的经验回归方程为=kx+b,则( )
A.k与r的符号相同 B.b与r的符号相同
C.k与r的符号相反 D.b与r的符号相反
2.(2020黑龙江齐齐哈尔高二下学期期末,)某工厂为研究某种产品的产量x(吨)与所需某种原材料y(吨)的相关性,在生产过程中收集了4组对应数据(x,y)如下表所示:(残差=观测值-预测值)
x 3 4 5 6
y 2.5 3 4 m
根据表中数据,得出y关于x的经验回归方程为=0.7x+a.据此计算出在样本点(4,3)处的残差为-0.15,则表中m的值为 .
3.(2020河南开封高二调研,)某相关部门推出了环境执法力度的评价与环境质量的评价系统,每项评价只有满意和不满意两个选项,市民可以随意进行评价,某工作人员利用随机抽样的方法抽取了200位市民的评价结果,发现对环境质量满意的占60%,对执法力度满意的占75%,其中对环境质量与执法力度都满意的有80人.
(1)依据α=0.001的独立性检验,分析环境质量与执法力度是否有关;
(2)为了改进工作作风,针对抽取的200位市民,从其中对执法力度不满意的人中随机抽取3位征求意见,用X表示3人中对环境质量与执法力度都不满意的人数,求X的分布列与均值.
附表及公式:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
4.(2020四川广元高三第一次高考适应性统考,)国家逐步推行全新的高考制度.新高考不再分文、理科,而是采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1 000名学生(其中男生550人,女生450人)中,采用分层随机抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中有女生45人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的物理和地理两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假设每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的2×2列联表.请将列联表补充完整,并依据α=0.01的独立性检验,分析选择科目与性别是否有关;
单位:人
选择物理 选择地理 合计
男生 10
女生 25
合计
(3)在抽取的选择地理的学生中用分层随机抽样的方法再抽取6名学生,然后从这6名学生中抽取2名学生了解他们对地理的选课意向情况,求2名学生中至少有1名男生的概率.
附表及公式:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
答案全解全析
8.1~8.3综合拔高练
五年高考练
1.D 观察散点图可知,散点图用光滑曲线连接起来比较接近对数型函数的图象,故选D.
2.解析 (1)由已知得样本平均数=yi=60,从而该地区这种野生动物数量的估计值为60×200=12 000.
(2)样本(xi,yi)(i=1,2,…,20)的相关系数
r===≈0.94.
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.
理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.
3.解析 (1)由题图中数据和附注中参考数据得=4,(ti-)2=28,=0.55,(ti-)(yi-)=tiyi-yi=40.17-4×9.32=2.89,
r≈≈0.99.
因为y与t的相关系数近似为0.99,说明y与t的线性相关程度相当高,从而可以用线性回归模型拟合y与t的关系.
(2)由=≈1.331及(1)得==≈0.10,
=-=1.331-0.10×4≈0.93.
所以y关于t的回归方程为=0.93+0.10t.
将2016年对应的t=9代入回归方程得=0.93+0.10×9=1.83.
所以预测2016年我国生活垃圾无害化处理量为1.83亿吨.
4.解析 (1)根据抽查数据,该市100天的空气中PM2.5浓度不超过75,且SO2浓度不超过150的天数为32+18+6+8=64,因此,该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150的概率的估计值为=0.64.
(2)根据抽查数据,可得2×2列联表:
SO2 PM2.5 [0,150] (150,475]
[0,75] 64 16
(75,115] 10 10
(3)根据(2)中的列联表得
K2=≈7.484.
由于7.484>6.635,故有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
5.解析 (1)由所给数据,该市一天的空气质量等级为1,2,3,4的概率的估计值如下表:
空气质量等级 1 2 3 4
概率的估计值 0.43 0.27 0.21 0.09
(2)一天中到该公园锻炼的平均人次的估计值为×(100×20+300×35+500×45)=350.
(3)根据所给数据,可得2×2列联表:
人次≤400 人次>400
空气质量好 33 37
空气质量不好 22 8
根据列联表得K2=≈5.820.
由于5.820>3.841,故有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
三年模拟练
1.A 若样本相关系数r为正,则两个变量呈现正相关,经验回归直线呈上升趋势;若样本相关系数r为负,则两个变量呈现负相关,经验回归直线呈下降趋势,∴k与r的符号相同.故选A.
2.答案 4.5
解析 由在样本点(4,3)处的残差为-0.15,可得=3.15,则3.15=0.7×4+a,解得a=0.35,由题意可知,产量x的平均数为=×(3+4+5+6)=4.5,由经验回归方程=0.7x+a过点(,),可得=0.7+a=0.7×4.5+a=3.15+a,则a=-3.15=×(9.5+m)-3.15,解得m=4.5.
3.解析 (1)对环境质量满意的有200×60%=120(人),对执法力度满意的有200×75%=150(人),对环境质量与执法力度都满意的有80人,由此可列出2×2列联表如下:
单位:人
对执法力 度满意 对执法力 度不满意 合计
对环境质 量满意 80 40 120
对环境质 量不满意 70 10 80
合计 150 50 200
零假设为H0:环境质量与执法力度无关.计算可得χ2==>10.828=x0.001,依据α=0.001的独立性检验,推断H0不成立,即认为环境质量与执法力度有关.
(2)X的可能取值为0,1,2,3,
P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,
则X的分布列为
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
4.解析 (1)由题意得,=,解得n=100,则抽取到的男生人数为550×=55.
(2)补充完整的2×2列联表如下:
单位:人
选择物理 选择地理 合计
男生 45 10 55
女生 25 20 45
合计 70 30 100
零假设为H0:选择科目与性别无关.计算可得χ2=≈8.129>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为选择科目与性别有关.
(3)从30名选择地理的学生中用分层随机抽样的方法抽取6名学生,
则这6名学生中有2名男生,4名女生,
设男生编号分别为1,2,女生编号分别为a,b,c,d,从这6名学生中抽取2名学生,
所有可能的结果为{ab,ac,ad,a1,a2,bc,bd,b1,b2,cd,c1,c2,d1,d2,12},共15种,
至少有一名男生的结果为{a1,a2,b1,b2,c1,c2,d1,d2,12},共9种,
所以2名学生中至少有1名男生的概率P==.
五年高考练
考点1 变量的相关关系与线性回归模型
1.(2020课标全国Ⅰ理,5,5分,)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
2.(2020课标全国Ⅱ理,18,12分,)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得xi=60,yi=1 200,(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
3.(2016课标全国Ⅲ,18,12分,)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:yi=9.32,tiyi=40.17,=0.55,≈2.646.
参考公式:相关系数r=,
回归方程=+t中斜率和截距最小二乘估计公式分别为:=,=-.
考点2 独立性检验及其应用
4.(2020新高考Ⅰ,19,12分,)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和SO2浓度(单位:μg/m3),得下表:
SO2 PM2.5 [0,50] (50,150] (150,475]
[0,35] 32 18 4
(35,75] 6 8 12
(75,115] 3 7 10
(1)估计事件“该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150”的概率;
(2)根据所给数据,完成下面的2×2列联表:
SO2 PM2.5 [0,150] (150,475]
[0,75]
(75,115]
(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
附:K2=,
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
.
5.(2020课标全国Ⅲ理,18,12分,)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 [0,200] (200,400] (400,600]
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
人次≤400 人次>400
空气质量好
空气质量不好
附:K2=,
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
.
三年模拟练
应用实践
1.(2020陕西西安八校联考,)设两个变量x和y之间线性相关,它们的样本相关系数为r,y关于x的经验回归方程为=kx+b,则( )
A.k与r的符号相同 B.b与r的符号相同
C.k与r的符号相反 D.b与r的符号相反
2.(2020黑龙江齐齐哈尔高二下学期期末,)某工厂为研究某种产品的产量x(吨)与所需某种原材料y(吨)的相关性,在生产过程中收集了4组对应数据(x,y)如下表所示:(残差=观测值-预测值)
x 3 4 5 6
y 2.5 3 4 m
根据表中数据,得出y关于x的经验回归方程为=0.7x+a.据此计算出在样本点(4,3)处的残差为-0.15,则表中m的值为 .
3.(2020河南开封高二调研,)某相关部门推出了环境执法力度的评价与环境质量的评价系统,每项评价只有满意和不满意两个选项,市民可以随意进行评价,某工作人员利用随机抽样的方法抽取了200位市民的评价结果,发现对环境质量满意的占60%,对执法力度满意的占75%,其中对环境质量与执法力度都满意的有80人.
(1)依据α=0.001的独立性检验,分析环境质量与执法力度是否有关;
(2)为了改进工作作风,针对抽取的200位市民,从其中对执法力度不满意的人中随机抽取3位征求意见,用X表示3人中对环境质量与执法力度都不满意的人数,求X的分布列与均值.
附表及公式:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
4.(2020四川广元高三第一次高考适应性统考,)国家逐步推行全新的高考制度.新高考不再分文、理科,而是采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1 000名学生(其中男生550人,女生450人)中,采用分层随机抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中有女生45人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的物理和地理两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假设每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的2×2列联表.请将列联表补充完整,并依据α=0.01的独立性检验,分析选择科目与性别是否有关;
单位:人
选择物理 选择地理 合计
男生 10
女生 25
合计
(3)在抽取的选择地理的学生中用分层随机抽样的方法再抽取6名学生,然后从这6名学生中抽取2名学生了解他们对地理的选课意向情况,求2名学生中至少有1名男生的概率.
附表及公式:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
答案全解全析
8.1~8.3综合拔高练
五年高考练
1.D 观察散点图可知,散点图用光滑曲线连接起来比较接近对数型函数的图象,故选D.
2.解析 (1)由已知得样本平均数=yi=60,从而该地区这种野生动物数量的估计值为60×200=12 000.
(2)样本(xi,yi)(i=1,2,…,20)的相关系数
r===≈0.94.
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.
理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.
3.解析 (1)由题图中数据和附注中参考数据得=4,(ti-)2=28,=0.55,(ti-)(yi-)=tiyi-yi=40.17-4×9.32=2.89,
r≈≈0.99.
因为y与t的相关系数近似为0.99,说明y与t的线性相关程度相当高,从而可以用线性回归模型拟合y与t的关系.
(2)由=≈1.331及(1)得==≈0.10,
=-=1.331-0.10×4≈0.93.
所以y关于t的回归方程为=0.93+0.10t.
将2016年对应的t=9代入回归方程得=0.93+0.10×9=1.83.
所以预测2016年我国生活垃圾无害化处理量为1.83亿吨.
4.解析 (1)根据抽查数据,该市100天的空气中PM2.5浓度不超过75,且SO2浓度不超过150的天数为32+18+6+8=64,因此,该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150的概率的估计值为=0.64.
(2)根据抽查数据,可得2×2列联表:
SO2 PM2.5 [0,150] (150,475]
[0,75] 64 16
(75,115] 10 10
(3)根据(2)中的列联表得
K2=≈7.484.
由于7.484>6.635,故有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
5.解析 (1)由所给数据,该市一天的空气质量等级为1,2,3,4的概率的估计值如下表:
空气质量等级 1 2 3 4
概率的估计值 0.43 0.27 0.21 0.09
(2)一天中到该公园锻炼的平均人次的估计值为×(100×20+300×35+500×45)=350.
(3)根据所给数据,可得2×2列联表:
人次≤400 人次>400
空气质量好 33 37
空气质量不好 22 8
根据列联表得K2=≈5.820.
由于5.820>3.841,故有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
三年模拟练
1.A 若样本相关系数r为正,则两个变量呈现正相关,经验回归直线呈上升趋势;若样本相关系数r为负,则两个变量呈现负相关,经验回归直线呈下降趋势,∴k与r的符号相同.故选A.
2.答案 4.5
解析 由在样本点(4,3)处的残差为-0.15,可得=3.15,则3.15=0.7×4+a,解得a=0.35,由题意可知,产量x的平均数为=×(3+4+5+6)=4.5,由经验回归方程=0.7x+a过点(,),可得=0.7+a=0.7×4.5+a=3.15+a,则a=-3.15=×(9.5+m)-3.15,解得m=4.5.
3.解析 (1)对环境质量满意的有200×60%=120(人),对执法力度满意的有200×75%=150(人),对环境质量与执法力度都满意的有80人,由此可列出2×2列联表如下:
单位:人
对执法力 度满意 对执法力 度不满意 合计
对环境质 量满意 80 40 120
对环境质 量不满意 70 10 80
合计 150 50 200
零假设为H0:环境质量与执法力度无关.计算可得χ2==>10.828=x0.001,依据α=0.001的独立性检验,推断H0不成立,即认为环境质量与执法力度有关.
(2)X的可能取值为0,1,2,3,
P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,
则X的分布列为
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
4.解析 (1)由题意得,=,解得n=100,则抽取到的男生人数为550×=55.
(2)补充完整的2×2列联表如下:
单位:人
选择物理 选择地理 合计
男生 45 10 55
女生 25 20 45
合计 70 30 100
零假设为H0:选择科目与性别无关.计算可得χ2=≈8.129>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为选择科目与性别有关.
(3)从30名选择地理的学生中用分层随机抽样的方法抽取6名学生,
则这6名学生中有2名男生,4名女生,
设男生编号分别为1,2,女生编号分别为a,b,c,d,从这6名学生中抽取2名学生,
所有可能的结果为{ab,ac,ad,a1,a2,bc,bd,b1,b2,cd,c1,c2,d1,d2,12},共15种,
至少有一名男生的结果为{a1,a2,b1,b2,c1,c2,d1,d2,12},共9种,
所以2名学生中至少有1名男生的概率P==.
