第八章成对数据的统计分析达标检测(Word含答案解析)
文档属性
| 名称 | 第八章成对数据的统计分析达标检测(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 244.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览




文档简介
本章达标检测
(满分:150分;时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法中正确的是( )
A.相关关系是一种不确定的关系,回归分析是对相关关系的分析,因此没有实际意义
B.独立性检验对分类变量关系的研究没有100%的把握,所以独立性检验研究的结果在实际中没有多大的实际意义
C.相关关系可以对变量的发展趋势进行预报,这种预报可能会是错误的
D.独立性检验如果得出的结论有99%的可信度,就意味着这个结论一定是正确的
2.若经验回归方程为=2-3.5x,则变量x增加一个单位,变量y平均( )
A.减少3.5个单位 B.增加2个单位
C.增加3.5个单位 D.减少2个单位
3.根据如下样本观测数据可得到的经验回归方程为=bx+a,则( )
x 3 4 5 6 7 8
y 4.0 2.5 -0.5 0.5 -2.0 -3.0
A.a>0,b<0 B.a>0,b>0
C.a<0,b<0 D.a<0,b>0
4.下图是变量x,y的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到经验回归方程:=b1x+a1,样本相关系数为r1;方案二:剔除点(10,32),根据剩下数据,得到经验回归方程:=b2x+a2,样本相关系数为r2,则( )
A.0C.-15.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
单位:人
男 女 合计
爱好 40 20 60
不爱好 20 30 50
合计 60 50 110
由χ2=算得χ2=≈7.8.
附表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
参照附表,得到的正确结论是( )
A.有99%以上的把握认为“爱好该项运动和性别有关”
B.有99%以上的把握认为“爱好该项运动和性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
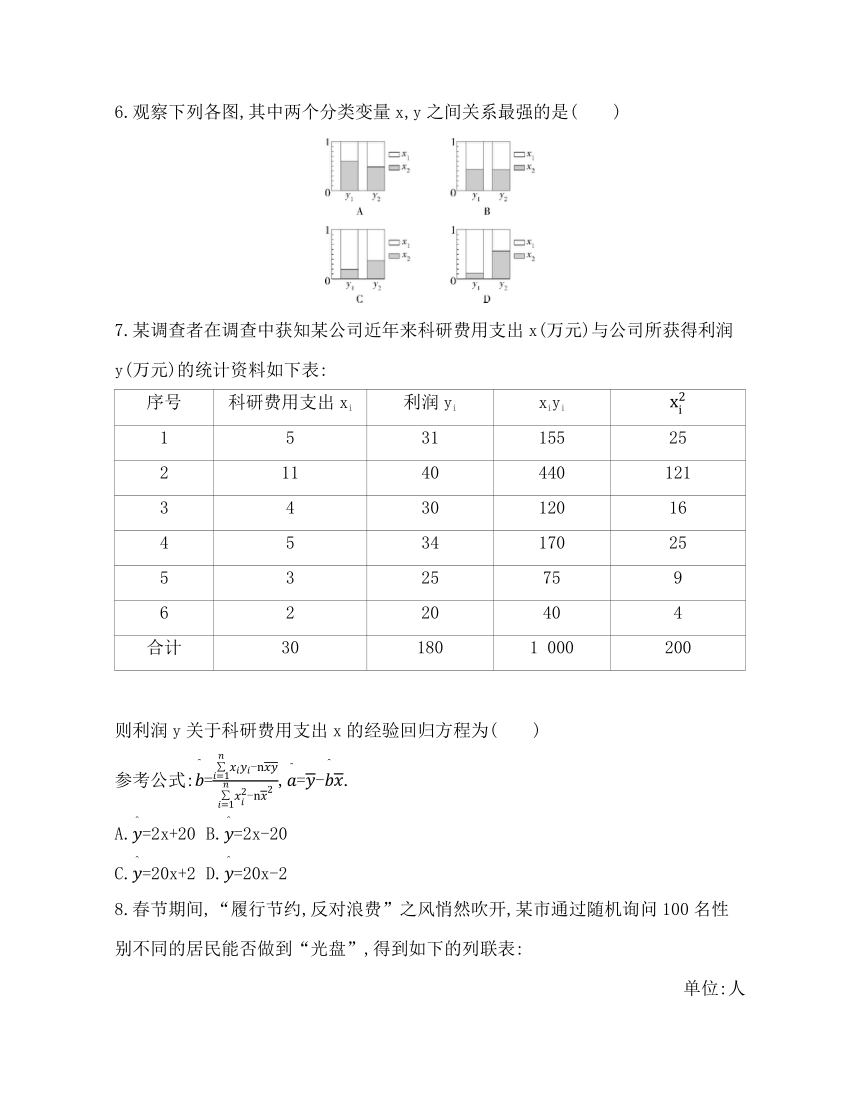
6.观察下列各图,其中两个分类变量x,y之间关系最强的是( )
7.某调查者在调查中获知某公司近年来科研费用支出x(万元)与公司所获得利润y(万元)的统计资料如下表:
序号 科研费用支出xi 利润yi xiyi
1 5 31 155 25
2 11 40 440 121
3 4 30 120 16
4 5 34 170 25
5 3 25 75 9
6 2 20 40 4
合计 30 180 1 000 200
则利润y关于科研费用支出x的经验回归方程为( )
参考公式:=,=-.
A.=2x+20 B.=2x-20
C.=20x+2 D.=20x-2
8.春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民能否做到“光盘”,得到如下的列联表:
单位:人
不能做到“光盘” 能做到“光盘” 合计
男 45 10 55
女 30 15 45
合计 75 25 100
附:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列说法正确的是( )
A.在回归分析中,可以借助散点图判断两个变量是否具有线性相关关系
B.在回归分析中,可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型的拟合效果越好
C.在回归分析模型中,样本相关系数的绝对值越大,说明模型的拟合效果越好
D.在经验回归方程=0.1x+10中,当解释变量x每增加1个单位时,响应变量增加0.1个单位
10.独立性检验中,为了调查变量X与变量Y的关系,经过计算得到χ2≥6.635=x0.01,其表示的意义是( )
A.有99%的把握认为变量X与变量Y没有关系
B.有1%的把握认为变量X与变量Y有关系
C.有99%的把握认为变量X与变量Y有关系
D.有1%的把握认为变量X与变量Y没有关系
11.已知由样本数据(xi,yi),i=1,2,…,n求得的经验回归方程为=1.5x+0.5,且=3,现发现两个样本点(1.2,2.2)和(4.8,7.8)误差较大,去除后重新求得的经验回归直线l的斜率为1.2,则( )
A.变量x与y具有正相关关系
B.去除后的经验回归方程为=1.2x+1.4
C.去除后y的估计值增加速度变快
D.去除后样本点(2,3.75)的残差为0.05
12.某校团委对“学生性别和喜欢运动是否有关”进行了一次调查,其中被调查的男、女生人数相同,男生喜欢运动的人数占男生人数的,女生喜欢运动的人数占女生人数的,若有95%的把握认为“是否喜欢运动和性别有关”,则被调查人中男生可能有( )
附:
α 0.05 0.01
xα 3.841 6.635
χ2=,其中n=a+b+c+d.
A.25人 B.45人 C.60人 D.75人
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.下列是关于男婴与女婴出生调查的列联表:
单位:人
晚上出生 白天出生 合计
男婴 45 A B
女婴 E 35 C
合计 98 D 180
那么A= ,B= ,C= ,D= ,E= .
14.已知样本容量为11,计算得xi=66,yi=132,经验回归方程为=0.3x+a,则a= .
15.某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了如下对照表,由表中数据得经验回归方程=x+,其中=-2.现预测当气温为-4 ℃时,用电量的度数为 .
气温x(℃) 18 13 10 -1
用电量y(度) 24 34 38 64
16.某部门通过随机调查89名工作人员的休闲方式是读书还是健身,得到的数据如下表:
单位:人
读书 健身 合计
女 24 31 55
男 8 26 34
合计 32 57 89
在犯错误的概率不超过 的前提下认为性别与休闲方式有关系.
附表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)2017年10月18日至10月24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级各随机抽取的100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩(单位:分)的频率分布直方图.
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;(同一组的数据用该组区间的中点值代表)
(2)完成下面的2×2列联表,并依据α=0.01的独立性检验,分析高一、高二两个年级学生这次读书读报知识竞赛的成绩是否有差异.
单位:人
成绩低于 60分 成绩不低于 60分 合计
高一年级
高二年级
合计
附: χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
18. (本小题满分12分)某连锁经营公司的5个零售店某月的销售额和利润如下表:
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润y/百万元 2 3 3 4 5
(1)画出散点图,观察散点图,说明两个变量是否线性相关;
(2)用最小二乘法计算利润y关于销售额x的经验回归方程;
(3)当销售额为4千万元时,估计利润为多少.
参考公式:=,=-.
19. (本小题满分12分)2020年3月,由于疫情的影响,各地学生在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,男生中有30人对线上教育满意,女生中有15人表示对线上教育不满意.
(1)完成下面的2×2列联表,依据α=0.01的独立性检验,分析对线上教育是否满意与性别是否有关;
单位:人
满意 不满意 合计
男生
女生
合计 120
(2)从被调查的对线上教育满意的学生中,利用分层随机抽样抽取8名学生,再在这8名学生中抽取3名学生作线上学习的经验介绍,其中抽取男生的人数为X,求X的分布列及期望.
附: χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
20. (本小题满分12分)某省级示范高中高三年级对各科考试的评价指标中有“难度系数”和“区分度”两个指标,难度系数=,区分度=.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147分,142分,137分;普通班三人的成绩分别为97分,102分,113分.通过样本估计本次考试的区分度(精确到0.01);
(2)该校高三年级6次数学考试的统计数据如下表:
难度系数x 0.64 0.71 0.74 0.76 0.77 0.82
区分度y 0.18 0.23 0.24 0.24 0.22 0.15
①计算样本相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01);
②令ti=|xi-0.74|(i=1,2,…,6),求出y关于t的经验回归方程,并预测x=0.75时y的值(精确到0.01).
附:xiyi=0.930 9,≈0.011 2,
tiyi=0.048 3,=0.007 3.
样本相关系数r=,
经验回归方程=x+的斜率和截距的最小二乘估计分别为=,=-.
21. (本小题满分12分)某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层随机抽样的方法从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到的频率分布直方图分别如图1,图2.
图1
图2
(1)从样本中日平均生产件数不足60的工人中随机抽取2人,求至少抽到一名25周岁以下组工人的概率;
(2)规定日平均生产件数不少于80者为生产能手,请你根据已知条件列出2×2列联表,依据α=0.1的独立性检验,分析生产能手与工人所在的年龄组是否有关.
附:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
22. (本小题满分12分)某地区在一次考试后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩x(单位:分)和物理成绩y(单位:分),绘制成如下散点图:
根据散点图可以看出y与x之间具有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于感冒导致物理考试发挥失常,B考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据进行处理,得到一些统计值:
xi=4 641,yi=3 108,xiyi=350 350,(xi-)2=13 814.5,(yi-)2=5 250,
其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的样本相关系数r≈0.81.
(1)若不剔除A,B两名考生的数据,用44组数据作回归分析,设此时y与x的样本相关系数为r0.试判断r0与r的大小关系,并说明理由;
(2)求y关于x的经验回归方程(精确到0.01),如果B考生加了这次物理考试(已知B考生的数学成绩为125分),估计其物理成绩是多少;(精确到个位)
(3)从概率统计规律看,本次考试该地区的物理成绩X服从正态分布N(μ,σ2).以剔除后的物理成绩作为样本,用样本平均数作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5 000名考生中,物理成绩位于区间[62.8,85.2]的人数Z的数学期望.(精确到个位)
附:①经验回归方程=x+中,=,=-.
②若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5.
③≈11.2.
答案全解全析
本章达标检测
一、单项选择题
1.C 相关关系虽然是一种不确定的关系,但是回归分析可以在某种程度上对变量的发展趋势进行预报,这种预报在尽量减小误差的条件下可以对生产与生活起到一定的指导作用,独立性检验对分类变量的研究也是不确定的,但是其结果也有一定的实际意义.故选C.
2.A 由经验回归方程可知=-3.5,则变量x增加一个单位,减少3.5个单位,即变量y平均减少3.5个单位.
3.A 依据题中的成对样本数据作散点图如下,由图可知,a>0,b<0.
4.A 观察散点图可知,变量x和y呈现正相关,所以0剔除点(10,32)之后,
可看出经验回归方程=b2x+a2拟合数据效果更好,所以r2更接近1.
所以05.A 因为χ2>6.635=x0.01,所以有99%以上的把握认为“爱好该项运动和性别有关”,故选A.
6.D 结合选项可知,D图中两个深色条的高相差最明显,说明两个分类变量之间关系最强.
7.A 设经验回归方程为=x+.
由题表中数据得,==2,
∴=30-2×5=20,
∴经验回归方程为=2x+20.
8.C χ2=
=≈3.030,
∵x0.1< χ2∴在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”.
二、多项选择题
9.ABD 对于A,可以借助散点图直观判断两个变量是否具有线性相关关系,所以正确;
对于B,可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,所以正确;
对于C,样本相关系数的绝对值越大,只能说明两个变量具有较强的相关性,不能作为分析模型的拟合效果好坏的依据,应该是R2越大,模型的拟合效果越好,所以错误;
对于D,在经验回归方程=0.1x+10中,当解释变量x每增加1个单位时,响应变量增加0.1个单位,所以正确.
故选ABD.
10.CD 独立性检验中, χ2≥6.635=x0.01,
它表示的意义是有1%的把握认为变量X与变量Y没有关系,D正确;
有99%的把握认为变量X与变量Y有关系,C正确.故选CD.
11.AB ∵=3,经验回归方程为=1.5x+0.5,∴=5,∵重新求得的经验回归直线l的斜率为1.2,∴变量x与y具有正相关关系,
设新的数据的所有横坐标的平均值为,纵坐标的平均值为,则(n-2)=n-(1.2+4.8)=3n-6=3(n-2),
(n-2)=n-(2.2+7.8)=5n-10=5(n-2),故=3,=5,
=-=5-1.2×3=1.4.
故新的经验回归方程为=1.2x+1.4,故A,B正确;
因为斜率为1.2不变,所以去除后y的估计值增长速度不变,C错误;
把x=2代入新的经验回归方程中,得=3.8,3.75-3.8=-0.05,故D错误.故选AB.
12.BC 设被调查人中男生有x人,依题意可得列联表如下:
单位:人
喜欢运动 不喜欢运动 合计
男生 x x x
女生 x x x
合计 x x 2x
若有95%的把握认为“是否喜欢运动和性别有关”,则3.841≤χ2=<6.635,解得40.330 5≤x<69.667 5,
由题意知x>0,且x是5的整数倍,所以结合选项知45和60满足题意.
故选BC.
三、填空题
13.答案 47;92;88;82;53
解析 ∵45+E=98,∴E=53.
∵E+35=C,∴C=88.
∵98+D=180,∴D=82.
∵A+35=D,∴A=47.
∵45+A=B,∴B=92.
14.答案 10.2
解析 ∵xi=66,yi=132,
∴=6,=12,∴a=12-0.3×6=10.2.
15.答案 68
解析 由题表中数据可得=×(18+13+10-1)=10,
=×(24+34+38+64)=40,
所以经验回归直线=-2x+过点(10,40),故=60.
所以当x=-4时,=-2×(-4)+60=68.
16.答案 0.1
解析 由题中列联表中的数据,得χ2=≈3.689,
因为χ2>2.706=x0.1,所以在犯错误的概率不超过0.1的前提下认为性别与休闲方式有关系.
四、解答题
17.解析 (1)高一年级参赛学生的平均成绩为(45×0.04+55×0.04+65×0.01+75×0.01)×10=54(分),高二年级参赛学生的平均成绩为(45×0.015+55×0.025+65×0.035+75×0.025)×10=62(分).(4分)
(2)补全2×2列联表如下:
单位:人
成绩低于 60分 成绩不低于 60分 合计
高一年级 80 20 100
高二年级 40 60 100
合计 120 80 200
零假设为H0:两个年级的成绩相互独立,即高一、高二两个年级学生这次读书读报知识竞赛的成绩没有差异.计算可得χ2=≈33.333>6.635=x0.01,根据α=0.01的独立性检验,推断H0不成立,即认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.(10分)
18.解析 (1)散点图如图所示.
由散点图可以看出变量x,y线性相关.(4分)
(2)设经验回归方程为=x+.
易得=3.4,=6,xiyi=112,=200,所以==0.5,
=-=3.4-0.5×6=0.4,
即利润y关于销售额x的经验回归方程为=0.5x+0.4.(9分)
(3)当销售额为4千万元时,利润约为0.5×4+0.4=2.4(百万元).(12分)
19.解析 (1)男生人数为120×=55,所以女生人数为120-55=65,
于是可完成2×2列联表如下:
单位:人
满意 不满意 合计
男生 30 25 55
女生 50 15 65
合计 80 40 120
(3分)
零假设为H0:对线上教育是否满意与性别无关.计算可得
χ2=≈6.713>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为对线上教育是否满意与性别有关.(6分)
(2)由(1)可知男生抽取3人,女生抽取5人,依题可知X的可能取值为0,1,2,3,并且X服从超几何分布,P(X=k)=(k=0,1,2,3),即
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==.(9分)
所以X的分布列为
X 0 1 2 3
P
可得E(X)=0×+1×+2×+3×=.(12分)
20.解析 (1)实验班三人成绩的平均值为142,
普通班三人成绩的平均值为104,故估计本次考试的区分度为≈0.25.(3分)
(2)①由题中的表格可知=×(0.64+0.71+0.74+0.76+0.77+0.82)=0.74,
=×(0.18+0.23+0.24+0.24+0.22+0.15)=0.21,
故r=≈-0.13.
因为|r|<0.75,所以相关性弱,故不能利用线性回归模型描述y与x的关系.(6分)
②y与t的对应数据如下表:
t 0.10 0.03 0 0.02 0.03 0.08
区分度y 0.18 0.23 0.24 0.24 0.22 0.15
则=≈≈-0.86,
所以=-≈0.21+0.86×≈0.25,
所以所求经验回归方程为=-0.86t+0.25,(10分)
当x=0.75时,t=0.01,则y≈0.24.(12分)
21.解析 (1)由已知得,样本中有25周岁以上组工人60名,25周岁以下组工人40名.
所以样本中日平均生产件数不足60的工人中,25周岁以上组工人有60×0.05=3(人),记为A1,A2,A3;25周岁以下组工人有40×0.05=2(人),记为B1,B2.
从中随机抽取2名工人,所有的可能结果共有10种,它们是(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).
其中,至少有1名25周岁以下组工人的可能结果共有7种,它们是(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),故所求概率P=.(5分)
(2)由题中频率分布直方图可知,在抽取的100名工人中,25周岁以上组中的生产能手有60×0.25=15(人),25周岁以下组中的生产能手有40×0.375=15(人),
据此可得2×2列联表如下:
单位:人
生产能手 非生产能手 合计
25周岁以上组 15 45 60
25周岁以下组 15 25 40
合计 30 70 100
(8分)
零假设为H0:生产能手与工人所在的年龄组无关.计算可得χ2=≈1.79<2.706=x0.1.(10分)
依据α=0.1的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即认为生产能手与工人所在的年龄组无关.(12分)
22.解析 (1)r0理由如下:由题图可知,y与x呈现正相关,
①异常点A,B会降低变量之间的线性相关程度.
②44个数据点与其经验回归直线的总偏差更大,回归效果更差,所以样本相关系数更小.
③42个数据点与其经验回归直线的总偏差更小,回归效果更好,所以样本相关系数更大.
④42个数据点更贴近其经验回归直线.
⑤44个数据点与其经验回归直线更离散.(4分)
(2)设y关于x的经验回归方程为=x+.由题中数据可得:=xi=110.5,
=yi=74,
所以(xi-)(yi-)=xiyi-42=350 350-42×110.5×74=6 916.
又因为(xi-)2=13 814.5,所以=≈0.50,
=-≈74-0.50×110.5≈18.75,
所以=0.50x+18.75.
将x=125代入,得y=0.50×125+18.75=62.5+18.75≈81,
所以估计B考生的物理成绩为81分.(8分)
(3)=yi=74,s2=(yi-)2=×5 250=125,
所以X~N(74,125),又因为≈11.2,
所以P(62.8≤X≤85.2)=P(74-11.2≤X≤74+11.2)≈0.682 7,
所以Z~B(5 000,0.682 7),所以E(Z)=5 000×0.682 7≈3 414,
即该地区本次考试物理成绩位于区间[62.8,85.2]的人数Z的数学期望约为3 414.(12分)
(满分:150分;时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法中正确的是( )
A.相关关系是一种不确定的关系,回归分析是对相关关系的分析,因此没有实际意义
B.独立性检验对分类变量关系的研究没有100%的把握,所以独立性检验研究的结果在实际中没有多大的实际意义
C.相关关系可以对变量的发展趋势进行预报,这种预报可能会是错误的
D.独立性检验如果得出的结论有99%的可信度,就意味着这个结论一定是正确的
2.若经验回归方程为=2-3.5x,则变量x增加一个单位,变量y平均( )
A.减少3.5个单位 B.增加2个单位
C.增加3.5个单位 D.减少2个单位
3.根据如下样本观测数据可得到的经验回归方程为=bx+a,则( )
x 3 4 5 6 7 8
y 4.0 2.5 -0.5 0.5 -2.0 -3.0
A.a>0,b<0 B.a>0,b>0
C.a<0,b<0 D.a<0,b>0
4.下图是变量x,y的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到经验回归方程:=b1x+a1,样本相关系数为r1;方案二:剔除点(10,32),根据剩下数据,得到经验回归方程:=b2x+a2,样本相关系数为r2,则( )
A.0
单位:人
男 女 合计
爱好 40 20 60
不爱好 20 30 50
合计 60 50 110
由χ2=算得χ2=≈7.8.
附表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
参照附表,得到的正确结论是( )
A.有99%以上的把握认为“爱好该项运动和性别有关”
B.有99%以上的把握认为“爱好该项运动和性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
6.观察下列各图,其中两个分类变量x,y之间关系最强的是( )
7.某调查者在调查中获知某公司近年来科研费用支出x(万元)与公司所获得利润y(万元)的统计资料如下表:
序号 科研费用支出xi 利润yi xiyi
1 5 31 155 25
2 11 40 440 121
3 4 30 120 16
4 5 34 170 25
5 3 25 75 9
6 2 20 40 4
合计 30 180 1 000 200
则利润y关于科研费用支出x的经验回归方程为( )
参考公式:=,=-.
A.=2x+20 B.=2x-20
C.=20x+2 D.=20x-2
8.春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民能否做到“光盘”,得到如下的列联表:
单位:人
不能做到“光盘” 能做到“光盘” 合计
男 45 10 55
女 30 15 45
合计 75 25 100
附:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列说法正确的是( )
A.在回归分析中,可以借助散点图判断两个变量是否具有线性相关关系
B.在回归分析中,可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型的拟合效果越好
C.在回归分析模型中,样本相关系数的绝对值越大,说明模型的拟合效果越好
D.在经验回归方程=0.1x+10中,当解释变量x每增加1个单位时,响应变量增加0.1个单位
10.独立性检验中,为了调查变量X与变量Y的关系,经过计算得到χ2≥6.635=x0.01,其表示的意义是( )
A.有99%的把握认为变量X与变量Y没有关系
B.有1%的把握认为变量X与变量Y有关系
C.有99%的把握认为变量X与变量Y有关系
D.有1%的把握认为变量X与变量Y没有关系
11.已知由样本数据(xi,yi),i=1,2,…,n求得的经验回归方程为=1.5x+0.5,且=3,现发现两个样本点(1.2,2.2)和(4.8,7.8)误差较大,去除后重新求得的经验回归直线l的斜率为1.2,则( )
A.变量x与y具有正相关关系
B.去除后的经验回归方程为=1.2x+1.4
C.去除后y的估计值增加速度变快
D.去除后样本点(2,3.75)的残差为0.05
12.某校团委对“学生性别和喜欢运动是否有关”进行了一次调查,其中被调查的男、女生人数相同,男生喜欢运动的人数占男生人数的,女生喜欢运动的人数占女生人数的,若有95%的把握认为“是否喜欢运动和性别有关”,则被调查人中男生可能有( )
附:
α 0.05 0.01
xα 3.841 6.635
χ2=,其中n=a+b+c+d.
A.25人 B.45人 C.60人 D.75人
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.下列是关于男婴与女婴出生调查的列联表:
单位:人
晚上出生 白天出生 合计
男婴 45 A B
女婴 E 35 C
合计 98 D 180
那么A= ,B= ,C= ,D= ,E= .
14.已知样本容量为11,计算得xi=66,yi=132,经验回归方程为=0.3x+a,则a= .
15.某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了如下对照表,由表中数据得经验回归方程=x+,其中=-2.现预测当气温为-4 ℃时,用电量的度数为 .
气温x(℃) 18 13 10 -1
用电量y(度) 24 34 38 64
16.某部门通过随机调查89名工作人员的休闲方式是读书还是健身,得到的数据如下表:
单位:人
读书 健身 合计
女 24 31 55
男 8 26 34
合计 32 57 89
在犯错误的概率不超过 的前提下认为性别与休闲方式有关系.
附表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)2017年10月18日至10月24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级各随机抽取的100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩(单位:分)的频率分布直方图.
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;(同一组的数据用该组区间的中点值代表)
(2)完成下面的2×2列联表,并依据α=0.01的独立性检验,分析高一、高二两个年级学生这次读书读报知识竞赛的成绩是否有差异.
单位:人
成绩低于 60分 成绩不低于 60分 合计
高一年级
高二年级
合计
附: χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
18. (本小题满分12分)某连锁经营公司的5个零售店某月的销售额和利润如下表:
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润y/百万元 2 3 3 4 5
(1)画出散点图,观察散点图,说明两个变量是否线性相关;
(2)用最小二乘法计算利润y关于销售额x的经验回归方程;
(3)当销售额为4千万元时,估计利润为多少.
参考公式:=,=-.
19. (本小题满分12分)2020年3月,由于疫情的影响,各地学生在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,男生中有30人对线上教育满意,女生中有15人表示对线上教育不满意.
(1)完成下面的2×2列联表,依据α=0.01的独立性检验,分析对线上教育是否满意与性别是否有关;
单位:人
满意 不满意 合计
男生
女生
合计 120
(2)从被调查的对线上教育满意的学生中,利用分层随机抽样抽取8名学生,再在这8名学生中抽取3名学生作线上学习的经验介绍,其中抽取男生的人数为X,求X的分布列及期望.
附: χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
20. (本小题满分12分)某省级示范高中高三年级对各科考试的评价指标中有“难度系数”和“区分度”两个指标,难度系数=,区分度=.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147分,142分,137分;普通班三人的成绩分别为97分,102分,113分.通过样本估计本次考试的区分度(精确到0.01);
(2)该校高三年级6次数学考试的统计数据如下表:
难度系数x 0.64 0.71 0.74 0.76 0.77 0.82
区分度y 0.18 0.23 0.24 0.24 0.22 0.15
①计算样本相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01);
②令ti=|xi-0.74|(i=1,2,…,6),求出y关于t的经验回归方程,并预测x=0.75时y的值(精确到0.01).
附:xiyi=0.930 9,≈0.011 2,
tiyi=0.048 3,=0.007 3.
样本相关系数r=,
经验回归方程=x+的斜率和截距的最小二乘估计分别为=,=-.
21. (本小题满分12分)某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层随机抽样的方法从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到的频率分布直方图分别如图1,图2.
图1
图2
(1)从样本中日平均生产件数不足60的工人中随机抽取2人,求至少抽到一名25周岁以下组工人的概率;
(2)规定日平均生产件数不少于80者为生产能手,请你根据已知条件列出2×2列联表,依据α=0.1的独立性检验,分析生产能手与工人所在的年龄组是否有关.
附:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
22. (本小题满分12分)某地区在一次考试后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩x(单位:分)和物理成绩y(单位:分),绘制成如下散点图:
根据散点图可以看出y与x之间具有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于感冒导致物理考试发挥失常,B考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据进行处理,得到一些统计值:
xi=4 641,yi=3 108,xiyi=350 350,(xi-)2=13 814.5,(yi-)2=5 250,
其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的样本相关系数r≈0.81.
(1)若不剔除A,B两名考生的数据,用44组数据作回归分析,设此时y与x的样本相关系数为r0.试判断r0与r的大小关系,并说明理由;
(2)求y关于x的经验回归方程(精确到0.01),如果B考生加了这次物理考试(已知B考生的数学成绩为125分),估计其物理成绩是多少;(精确到个位)
(3)从概率统计规律看,本次考试该地区的物理成绩X服从正态分布N(μ,σ2).以剔除后的物理成绩作为样本,用样本平均数作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5 000名考生中,物理成绩位于区间[62.8,85.2]的人数Z的数学期望.(精确到个位)
附:①经验回归方程=x+中,=,=-.
②若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5.
③≈11.2.
答案全解全析
本章达标检测
一、单项选择题
1.C 相关关系虽然是一种不确定的关系,但是回归分析可以在某种程度上对变量的发展趋势进行预报,这种预报在尽量减小误差的条件下可以对生产与生活起到一定的指导作用,独立性检验对分类变量的研究也是不确定的,但是其结果也有一定的实际意义.故选C.
2.A 由经验回归方程可知=-3.5,则变量x增加一个单位,减少3.5个单位,即变量y平均减少3.5个单位.
3.A 依据题中的成对样本数据作散点图如下,由图可知,a>0,b<0.
4.A 观察散点图可知,变量x和y呈现正相关,所以0
可看出经验回归方程=b2x+a2拟合数据效果更好,所以r2更接近1.
所以0
6.D 结合选项可知,D图中两个深色条的高相差最明显,说明两个分类变量之间关系最强.
7.A 设经验回归方程为=x+.
由题表中数据得,==2,
∴=30-2×5=20,
∴经验回归方程为=2x+20.
8.C χ2=
=≈3.030,
∵x0.1< χ2
二、多项选择题
9.ABD 对于A,可以借助散点图直观判断两个变量是否具有线性相关关系,所以正确;
对于B,可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,所以正确;
对于C,样本相关系数的绝对值越大,只能说明两个变量具有较强的相关性,不能作为分析模型的拟合效果好坏的依据,应该是R2越大,模型的拟合效果越好,所以错误;
对于D,在经验回归方程=0.1x+10中,当解释变量x每增加1个单位时,响应变量增加0.1个单位,所以正确.
故选ABD.
10.CD 独立性检验中, χ2≥6.635=x0.01,
它表示的意义是有1%的把握认为变量X与变量Y没有关系,D正确;
有99%的把握认为变量X与变量Y有关系,C正确.故选CD.
11.AB ∵=3,经验回归方程为=1.5x+0.5,∴=5,∵重新求得的经验回归直线l的斜率为1.2,∴变量x与y具有正相关关系,
设新的数据的所有横坐标的平均值为,纵坐标的平均值为,则(n-2)=n-(1.2+4.8)=3n-6=3(n-2),
(n-2)=n-(2.2+7.8)=5n-10=5(n-2),故=3,=5,
=-=5-1.2×3=1.4.
故新的经验回归方程为=1.2x+1.4,故A,B正确;
因为斜率为1.2不变,所以去除后y的估计值增长速度不变,C错误;
把x=2代入新的经验回归方程中,得=3.8,3.75-3.8=-0.05,故D错误.故选AB.
12.BC 设被调查人中男生有x人,依题意可得列联表如下:
单位:人
喜欢运动 不喜欢运动 合计
男生 x x x
女生 x x x
合计 x x 2x
若有95%的把握认为“是否喜欢运动和性别有关”,则3.841≤χ2=<6.635,解得40.330 5≤x<69.667 5,
由题意知x>0,且x是5的整数倍,所以结合选项知45和60满足题意.
故选BC.
三、填空题
13.答案 47;92;88;82;53
解析 ∵45+E=98,∴E=53.
∵E+35=C,∴C=88.
∵98+D=180,∴D=82.
∵A+35=D,∴A=47.
∵45+A=B,∴B=92.
14.答案 10.2
解析 ∵xi=66,yi=132,
∴=6,=12,∴a=12-0.3×6=10.2.
15.答案 68
解析 由题表中数据可得=×(18+13+10-1)=10,
=×(24+34+38+64)=40,
所以经验回归直线=-2x+过点(10,40),故=60.
所以当x=-4时,=-2×(-4)+60=68.
16.答案 0.1
解析 由题中列联表中的数据,得χ2=≈3.689,
因为χ2>2.706=x0.1,所以在犯错误的概率不超过0.1的前提下认为性别与休闲方式有关系.
四、解答题
17.解析 (1)高一年级参赛学生的平均成绩为(45×0.04+55×0.04+65×0.01+75×0.01)×10=54(分),高二年级参赛学生的平均成绩为(45×0.015+55×0.025+65×0.035+75×0.025)×10=62(分).(4分)
(2)补全2×2列联表如下:
单位:人
成绩低于 60分 成绩不低于 60分 合计
高一年级 80 20 100
高二年级 40 60 100
合计 120 80 200
零假设为H0:两个年级的成绩相互独立,即高一、高二两个年级学生这次读书读报知识竞赛的成绩没有差异.计算可得χ2=≈33.333>6.635=x0.01,根据α=0.01的独立性检验,推断H0不成立,即认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.(10分)
18.解析 (1)散点图如图所示.
由散点图可以看出变量x,y线性相关.(4分)
(2)设经验回归方程为=x+.
易得=3.4,=6,xiyi=112,=200,所以==0.5,
=-=3.4-0.5×6=0.4,
即利润y关于销售额x的经验回归方程为=0.5x+0.4.(9分)
(3)当销售额为4千万元时,利润约为0.5×4+0.4=2.4(百万元).(12分)
19.解析 (1)男生人数为120×=55,所以女生人数为120-55=65,
于是可完成2×2列联表如下:
单位:人
满意 不满意 合计
男生 30 25 55
女生 50 15 65
合计 80 40 120
(3分)
零假设为H0:对线上教育是否满意与性别无关.计算可得
χ2=≈6.713>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为对线上教育是否满意与性别有关.(6分)
(2)由(1)可知男生抽取3人,女生抽取5人,依题可知X的可能取值为0,1,2,3,并且X服从超几何分布,P(X=k)=(k=0,1,2,3),即
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==.(9分)
所以X的分布列为
X 0 1 2 3
P
可得E(X)=0×+1×+2×+3×=.(12分)
20.解析 (1)实验班三人成绩的平均值为142,
普通班三人成绩的平均值为104,故估计本次考试的区分度为≈0.25.(3分)
(2)①由题中的表格可知=×(0.64+0.71+0.74+0.76+0.77+0.82)=0.74,
=×(0.18+0.23+0.24+0.24+0.22+0.15)=0.21,
故r=≈-0.13.
因为|r|<0.75,所以相关性弱,故不能利用线性回归模型描述y与x的关系.(6分)
②y与t的对应数据如下表:
t 0.10 0.03 0 0.02 0.03 0.08
区分度y 0.18 0.23 0.24 0.24 0.22 0.15
则=≈≈-0.86,
所以=-≈0.21+0.86×≈0.25,
所以所求经验回归方程为=-0.86t+0.25,(10分)
当x=0.75时,t=0.01,则y≈0.24.(12分)
21.解析 (1)由已知得,样本中有25周岁以上组工人60名,25周岁以下组工人40名.
所以样本中日平均生产件数不足60的工人中,25周岁以上组工人有60×0.05=3(人),记为A1,A2,A3;25周岁以下组工人有40×0.05=2(人),记为B1,B2.
从中随机抽取2名工人,所有的可能结果共有10种,它们是(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).
其中,至少有1名25周岁以下组工人的可能结果共有7种,它们是(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),故所求概率P=.(5分)
(2)由题中频率分布直方图可知,在抽取的100名工人中,25周岁以上组中的生产能手有60×0.25=15(人),25周岁以下组中的生产能手有40×0.375=15(人),
据此可得2×2列联表如下:
单位:人
生产能手 非生产能手 合计
25周岁以上组 15 45 60
25周岁以下组 15 25 40
合计 30 70 100
(8分)
零假设为H0:生产能手与工人所在的年龄组无关.计算可得χ2=≈1.79<2.706=x0.1.(10分)
依据α=0.1的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即认为生产能手与工人所在的年龄组无关.(12分)
22.解析 (1)r0
①异常点A,B会降低变量之间的线性相关程度.
②44个数据点与其经验回归直线的总偏差更大,回归效果更差,所以样本相关系数更小.
③42个数据点与其经验回归直线的总偏差更小,回归效果更好,所以样本相关系数更大.
④42个数据点更贴近其经验回归直线.
⑤44个数据点与其经验回归直线更离散.(4分)
(2)设y关于x的经验回归方程为=x+.由题中数据可得:=xi=110.5,
=yi=74,
所以(xi-)(yi-)=xiyi-42=350 350-42×110.5×74=6 916.
又因为(xi-)2=13 814.5,所以=≈0.50,
=-≈74-0.50×110.5≈18.75,
所以=0.50x+18.75.
将x=125代入,得y=0.50×125+18.75=62.5+18.75≈81,
所以估计B考生的物理成绩为81分.(8分)
(3)=yi=74,s2=(yi-)2=×5 250=125,
所以X~N(74,125),又因为≈11.2,
所以P(62.8≤X≤85.2)=P(74-11.2≤X≤74+11.2)≈0.682 7,
所以Z~B(5 000,0.682 7),所以E(Z)=5 000×0.682 7≈3 414,
即该地区本次考试物理成绩位于区间[62.8,85.2]的人数Z的数学期望约为3 414.(12分)
