专题强化练8 独立性检验与统计、概率的综合应用 (Word版含解析)
文档属性
| 名称 | 专题强化练8 独立性检验与统计、概率的综合应用 (Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 99.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 21:59:17 | ||
图片预览



文档简介
专题强化练8 独立性检验与统计、概率的综合应用
解答题
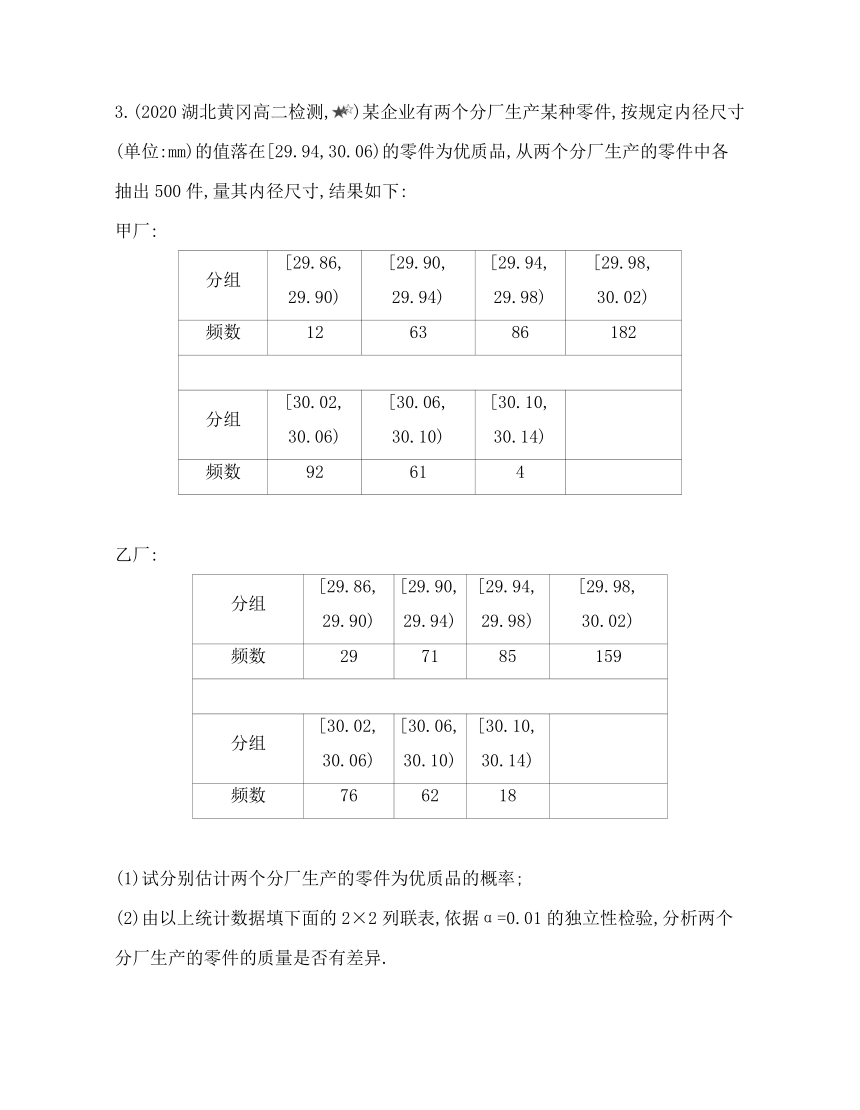
1.(2020四川南充高三适应性考试,)为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高(单位:厘米)进行统计,统计结果如下表所示,设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
茎高(厘米)
抗倒伏 143 147 147 151 153 153 157 159 160 164 166 169 174
175 175 180 188 188 192 195 195 199 203 206 206
茎高(厘米)
易倒伏 151 167 175 178 181 182 186 186 187 190
190 193 194 195 198 199 199 202 202 203
(1)求出易倒伏玉米茎高的中位数m;
(2)根据表格中的数据,完成下面的列联表:
抗倒伏 易倒伏 合计
矮茎
高茎
合计
(3)根据(2)中的列联表,依据α=0.01的独立性检验,分析抗倒伏与玉米矮茎是否有关.
附:χ2=,其中n=a+b+c+d.
α 0.05 0.01 0.001
xα 3.841 6.635 10.828
2.(2020河南安阳高三二模,)截至2019年,由新华社《瞭望东方周刊》与瞭望智库共同主办的“中国最具幸福感城市”调查推选活动已连续成功举办12年,累计推选出60余座幸福城市,全国9亿多人次参与调查,使“城市幸福感”概念深入人心.为了便于对某城市的“城市幸福感”指数进行研究,现从该市抽取若干人进行调查,绘制成如下表所示不完整的2×2列联表(数据单位:人).
男 女 合计
非常幸福 11 15
比较幸福 9
合计 30
(1)将列联表补充完整,并依据α=0.1的独立性检验,分析“城市幸福感”指数与性别是否有关;
(2)若感觉“非常幸福”记2分,“比较幸福”记1分,从上表男性中随机抽取3人,记3人得分之和为X,求X的分布列,并根据分布列求X≤4的概率.
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.001
xα 2.706 3.841 6.635 10.828
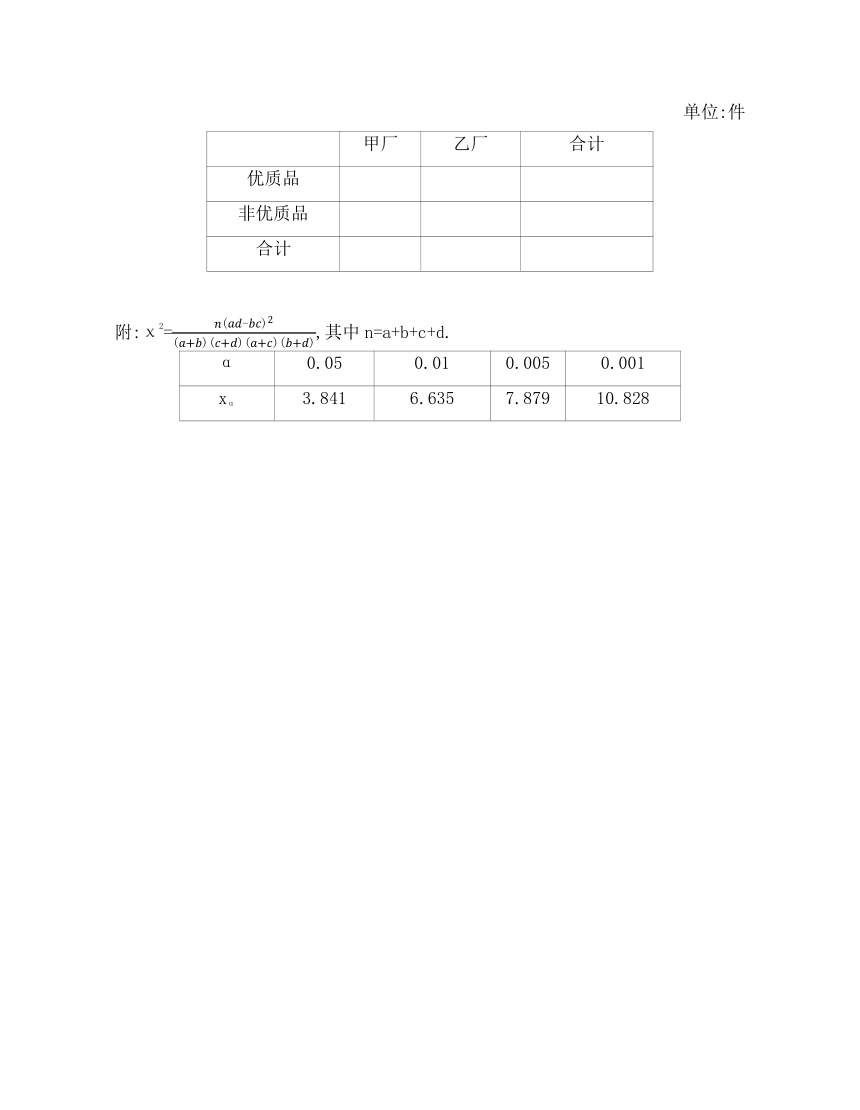
3.(2020湖北黄冈高二检测,)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品,从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如下:
甲厂:
分组 [29.86, 29.90) [29.90, 29.94) [29.94, 29.98) [29.98, 30.02)
频数 12 63 86 182
分组 [30.02, 30.06) [30.06, 30.10) [30.10, 30.14)
频数 92 61 4
乙厂:
分组 [29.86, 29.90) [29.90, 29.94) [29.94, 29.98) [29.98, 30.02)
频数 29 71 85 159
分组 [30.02, 30.06) [30.06, 30.10) [30.10, 30.14)
频数 76 62 18
(1)试分别估计两个分厂生产的零件为优质品的概率;
(2)由以上统计数据填下面的2×2列联表,依据α=0.01的独立性检验,分析两个分厂生产的零件的质量是否有差异.
单位:件
甲厂 乙厂 合计
优质品
非优质品
合计
附:χ2=,其中n=a+b+c+d.
α 0.05 0.01 0.005 0.001
xα 3.841 6.635 7.879 10.828
4.(2020福建泉州高三质量检测,)冬天的北方室外温度极低,若轻薄保暖的石墨烯发热膜能用在衣服上,可爱的医务工作者行动会更方便.石墨烯发热膜的制作:从石墨中分离出石墨烯,制成石墨烯发热膜.从石墨中分离石墨烯的一种方法是化学气相沉积法,使石墨升华后附着在材料上再结晶.现在有A材料、B材料可供选择,研究人员对附着在A材料、B材料上的石墨各做了50次再结晶试验,得到如下等高堆积条形图.
(1)根据等高堆积条形图,填写如下列联表,并依据α=0.01的独立性检验,分析试验结果与材料是否有关;
单位:次
A材料 B材料 合计
试验成功
试验不成功
合计
(2)研究人员得到石墨烯后,再制作石墨烯发热膜有三个环节:①透明基底及UV胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为,第三环节生产合格的概率为,且各生产环节相互独立.已知生产1吨石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三环节的修复费用为3 000元,其余环节修复费用均为1 000元.试问如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
答案全解全析
专题强化练8 独立性检验与
统计、概率的综合应用
解答题
1.解析 (1)m==190.
(2)补全的列联表如下所示:
抗倒伏 易倒伏 合计
矮茎 15 4 19
高茎 10 16 26
合计 25 20 45
(3)零假设为H0:抗倒伏与玉米矮茎无关.计算可得χ2=≈7.287>6.635=x0.01,依据α=0.01的独立性检验,推断H0不成立,即认为抗倒伏与玉米矮茎有关.
2.解析 (1)补充完整的表格如下所示:
男 女 合计
非常幸福 4 11 15
比较幸福 6 9 15
合计 10 20 30
零假设为H0:“城市幸福感”指数与性别无关.计算可得χ2==0.6<2.706=x0.1,
依据α=0.1的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为“城市幸福感”指数与性别无关.
(2)由题可知,X的可能取值有3,4,5,6,
P(X=3)==,P(X=4)==,P(X=5)==,P(X=6)==,
所以X的分布列为
X 3 4 5 6
P
所以P(X≤4)=P(X=3)+P(X=4)=+=.
3.解析 (1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件为优质品的概率约为×100%=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件为优质品的概率约为×100%=64%.
(2)单位:件
甲厂 乙厂 合计
优质品 360 320 680
非优质品 140 180 320
合计 500 500 1 000
零假设为H0:两个分厂生产的零件的质量无差异.由表中数据得χ2=≈7.35>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为两个分厂生产的零件的质量有差异.
4.解析 (1)根据题中所给等高堆积条形图,得列联表如下:
单位:次
A材料 B材料 合计
试验成功 45 30 75
试验不成功 5 20 25
合计 50 50 100
零假设为H0:试验结果与材料无关.计算可得χ2==12>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为试验结果与材料有关.
(2)设生产1吨石墨烯发热膜所需的修复费用为X万元.
易知X的可能取值为0,0.1,0.2,0.3,0.4,0.5.
P(X=0)=×=,
P(X=0.1)=×=,
P(X=0.2)=×=,
P(X=0.3)=×=,
P(X=0.4)=×=,
P(X=0.5)=×=,
则X的分布列为
X 0 0.1 0.2 0.3 0.4 0.5
P
修复费用X的期望E(X)=0×+0.1×+0.2×+0.3×+0.4×+0.5×=0.2.
所以石墨烯发热膜的定价至少为0.2+1+1=2.2万元/吨,才能实现预期的利润目标.
解答题
1.(2020四川南充高三适应性考试,)为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高(单位:厘米)进行统计,统计结果如下表所示,设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
茎高(厘米)
抗倒伏 143 147 147 151 153 153 157 159 160 164 166 169 174
175 175 180 188 188 192 195 195 199 203 206 206
茎高(厘米)
易倒伏 151 167 175 178 181 182 186 186 187 190
190 193 194 195 198 199 199 202 202 203
(1)求出易倒伏玉米茎高的中位数m;
(2)根据表格中的数据,完成下面的列联表:
抗倒伏 易倒伏 合计
矮茎
高茎
合计
(3)根据(2)中的列联表,依据α=0.01的独立性检验,分析抗倒伏与玉米矮茎是否有关.
附:χ2=,其中n=a+b+c+d.
α 0.05 0.01 0.001
xα 3.841 6.635 10.828
2.(2020河南安阳高三二模,)截至2019年,由新华社《瞭望东方周刊》与瞭望智库共同主办的“中国最具幸福感城市”调查推选活动已连续成功举办12年,累计推选出60余座幸福城市,全国9亿多人次参与调查,使“城市幸福感”概念深入人心.为了便于对某城市的“城市幸福感”指数进行研究,现从该市抽取若干人进行调查,绘制成如下表所示不完整的2×2列联表(数据单位:人).
男 女 合计
非常幸福 11 15
比较幸福 9
合计 30
(1)将列联表补充完整,并依据α=0.1的独立性检验,分析“城市幸福感”指数与性别是否有关;
(2)若感觉“非常幸福”记2分,“比较幸福”记1分,从上表男性中随机抽取3人,记3人得分之和为X,求X的分布列,并根据分布列求X≤4的概率.
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.001
xα 2.706 3.841 6.635 10.828
3.(2020湖北黄冈高二检测,)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品,从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如下:
甲厂:
分组 [29.86, 29.90) [29.90, 29.94) [29.94, 29.98) [29.98, 30.02)
频数 12 63 86 182
分组 [30.02, 30.06) [30.06, 30.10) [30.10, 30.14)
频数 92 61 4
乙厂:
分组 [29.86, 29.90) [29.90, 29.94) [29.94, 29.98) [29.98, 30.02)
频数 29 71 85 159
分组 [30.02, 30.06) [30.06, 30.10) [30.10, 30.14)
频数 76 62 18
(1)试分别估计两个分厂生产的零件为优质品的概率;
(2)由以上统计数据填下面的2×2列联表,依据α=0.01的独立性检验,分析两个分厂生产的零件的质量是否有差异.
单位:件
甲厂 乙厂 合计
优质品
非优质品
合计
附:χ2=,其中n=a+b+c+d.
α 0.05 0.01 0.005 0.001
xα 3.841 6.635 7.879 10.828
4.(2020福建泉州高三质量检测,)冬天的北方室外温度极低,若轻薄保暖的石墨烯发热膜能用在衣服上,可爱的医务工作者行动会更方便.石墨烯发热膜的制作:从石墨中分离出石墨烯,制成石墨烯发热膜.从石墨中分离石墨烯的一种方法是化学气相沉积法,使石墨升华后附着在材料上再结晶.现在有A材料、B材料可供选择,研究人员对附着在A材料、B材料上的石墨各做了50次再结晶试验,得到如下等高堆积条形图.
(1)根据等高堆积条形图,填写如下列联表,并依据α=0.01的独立性检验,分析试验结果与材料是否有关;
单位:次
A材料 B材料 合计
试验成功
试验不成功
合计
(2)研究人员得到石墨烯后,再制作石墨烯发热膜有三个环节:①透明基底及UV胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为,第三环节生产合格的概率为,且各生产环节相互独立.已知生产1吨石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三环节的修复费用为3 000元,其余环节修复费用均为1 000元.试问如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
答案全解全析
专题强化练8 独立性检验与
统计、概率的综合应用
解答题
1.解析 (1)m==190.
(2)补全的列联表如下所示:
抗倒伏 易倒伏 合计
矮茎 15 4 19
高茎 10 16 26
合计 25 20 45
(3)零假设为H0:抗倒伏与玉米矮茎无关.计算可得χ2=≈7.287>6.635=x0.01,依据α=0.01的独立性检验,推断H0不成立,即认为抗倒伏与玉米矮茎有关.
2.解析 (1)补充完整的表格如下所示:
男 女 合计
非常幸福 4 11 15
比较幸福 6 9 15
合计 10 20 30
零假设为H0:“城市幸福感”指数与性别无关.计算可得χ2==0.6<2.706=x0.1,
依据α=0.1的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为“城市幸福感”指数与性别无关.
(2)由题可知,X的可能取值有3,4,5,6,
P(X=3)==,P(X=4)==,P(X=5)==,P(X=6)==,
所以X的分布列为
X 3 4 5 6
P
所以P(X≤4)=P(X=3)+P(X=4)=+=.
3.解析 (1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件为优质品的概率约为×100%=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件为优质品的概率约为×100%=64%.
(2)单位:件
甲厂 乙厂 合计
优质品 360 320 680
非优质品 140 180 320
合计 500 500 1 000
零假设为H0:两个分厂生产的零件的质量无差异.由表中数据得χ2=≈7.35>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为两个分厂生产的零件的质量有差异.
4.解析 (1)根据题中所给等高堆积条形图,得列联表如下:
单位:次
A材料 B材料 合计
试验成功 45 30 75
试验不成功 5 20 25
合计 50 50 100
零假设为H0:试验结果与材料无关.计算可得χ2==12>6.635=x0.01,
依据α=0.01的独立性检验,推断H0不成立,即认为试验结果与材料有关.
(2)设生产1吨石墨烯发热膜所需的修复费用为X万元.
易知X的可能取值为0,0.1,0.2,0.3,0.4,0.5.
P(X=0)=×=,
P(X=0.1)=×=,
P(X=0.2)=×=,
P(X=0.3)=×=,
P(X=0.4)=×=,
P(X=0.5)=×=,
则X的分布列为
X 0 0.1 0.2 0.3 0.4 0.5
P
修复费用X的期望E(X)=0×+0.1×+0.2×+0.3×+0.4×+0.5×=0.2.
所以石墨烯发热膜的定价至少为0.2+1+1=2.2万元/吨,才能实现预期的利润目标.
