5.2.2导数的四则运算法则 课件(共23张PPT)
文档属性
| 名称 | 5.2.2导数的四则运算法则 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 21:24:54 | ||
图片预览







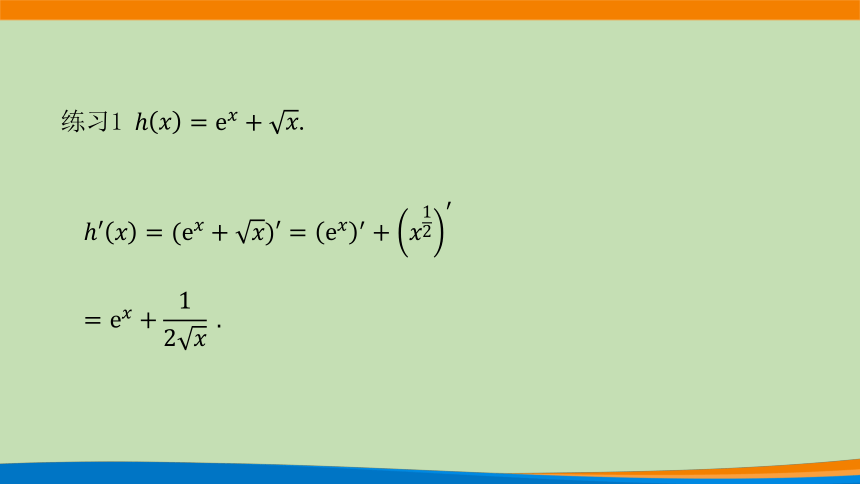

文档简介
(共23张PPT)
5.2.2 导数的四则运算法则
人教A版 选择性必修第二册
第五章 一元函数的导数及其应用
学习目标:
1. 理解并掌握导数的四则运算法则;
2. 用导数的四则运算法则求简单函数的导数.
教学重点:
能灵活运用导数的四则运算法则求函数导数.
教学难点:
函数积、商的求导法则.
问题1 我们怎样求一个函数的导数?
导数的定义(求增量、算比值、求极限);
直接通过公式得到基本初等函数的导数.
问题2 如何求函数的导数?
问题探究
目前,我们只能通过定义来求其导数.
设,由导数的定义,
问题3 观察,,;与导数,,.你有什么发现和猜想?
;.
大胆猜想:.
所以
所以
即
同理可证:
所以
小心论证设 f (x) ,g (x) 均为可导函数, y = f (x) + g (x) 则
一般地,对于两个函数的和(或差)的导数,我们有如下法则:
函数和、差的求导运算法则
总结归纳
(课本P76)例1求下列函数的导数:
(1);(2);
例题讲解
解:(1)
(2)
练习1.
问题4 以,为例,计算与,看看是否相等?
追问:再验算与商的导数是否等于它们导数的商?
,,
所以.
小心论证 设 f (x) ,g (x) 均为可导函数,y = f (x) . g (x) 则
所以
所以
即
所以
同理可证 设 f (x),g (x) 均为可导函数,y=
所以
所以
即
所以
事实上,对于两个函数的乘积(或商)的导数,我们有如下法则:
函数积、商的求导运算法则
由函数乘积的导数法则可以得出
也就是说,常数与函数的积的导数,等于常数与函数的导数的积,即:
(课本P77)例2 求下列函数的导数:
;
解:(1)
总结
求函数的导数的策略
(1)利用函数的和、差、积、商的求导法则求函数的导数时,要分清函数的结构,再利用相应的法则进行求导.
(2)遇到函数的表达式是乘积形式或是商的形式,有时先将函数表达式展开或化简,然后再求导.
练习2 求的导数
(课本P77)例3日常生活中的饮用水通常是经过净化的. 随着水的纯净度的提高,所需净化费用不断增加. 已知将吨水净化到纯净度为时所需费用(单位:元)为
1.求净化到下列纯净度,所需净化费用的瞬时变化率;
(1) (2).
解
所以
(1)因为,所以净化到纯净度为,净化费用的瞬时变化率为元/吨.
(2)因为,所以净化到纯净度为,净化费用的瞬时变化率为21元/吨.
2.根据计算结果能得出哪些结论?
净化到纯净度为时净化费用的变化率是净化到纯净度为时的倍.
即净化到纯净度为98%时净化费用变化的快慢是净化到纯净度为90%时净化费用变化快慢的倍.
这说明水的纯净度越高,需要的净化费用就越多,而且净化费用增加的速度也越快。
(1).
例4 已知函数
(1)求函数的导数
(2)求函数的图象在处的切线方程.
(2)由题意可知切点的横坐标为,
所以切线的斜率是,
切点纵坐标为,
故切点的坐标是,
所以切线方程为,即.
问题5 我们学习了哪些知识内容?
导数的四则运算法则及运用导数的四则运算法则求函数的导数.
追问: 你有什么感受?
运用函数的导数运算法则求函数的导数,比用导数定义求函数的导数要方便很多.
运用导数运算法则可以求很多初等函数的导数,这有助于研究更多函数的性质.
基础题组 课本P78练习123
拔高题组课本P81习题5.2 456
课后作业
再会!
5.2.2 导数的四则运算法则
人教A版 选择性必修第二册
第五章 一元函数的导数及其应用
学习目标:
1. 理解并掌握导数的四则运算法则;
2. 用导数的四则运算法则求简单函数的导数.
教学重点:
能灵活运用导数的四则运算法则求函数导数.
教学难点:
函数积、商的求导法则.
问题1 我们怎样求一个函数的导数?
导数的定义(求增量、算比值、求极限);
直接通过公式得到基本初等函数的导数.
问题2 如何求函数的导数?
问题探究
目前,我们只能通过定义来求其导数.
设,由导数的定义,
问题3 观察,,;与导数,,.你有什么发现和猜想?
;.
大胆猜想:.
所以
所以
即
同理可证:
所以
小心论证设 f (x) ,g (x) 均为可导函数, y = f (x) + g (x) 则
一般地,对于两个函数的和(或差)的导数,我们有如下法则:
函数和、差的求导运算法则
总结归纳
(课本P76)例1求下列函数的导数:
(1);(2);
例题讲解
解:(1)
(2)
练习1.
问题4 以,为例,计算与,看看是否相等?
追问:再验算与商的导数是否等于它们导数的商?
,,
所以.
小心论证 设 f (x) ,g (x) 均为可导函数,y = f (x) . g (x) 则
所以
所以
即
所以
同理可证 设 f (x),g (x) 均为可导函数,y=
所以
所以
即
所以
事实上,对于两个函数的乘积(或商)的导数,我们有如下法则:
函数积、商的求导运算法则
由函数乘积的导数法则可以得出
也就是说,常数与函数的积的导数,等于常数与函数的导数的积,即:
(课本P77)例2 求下列函数的导数:
;
解:(1)
总结
求函数的导数的策略
(1)利用函数的和、差、积、商的求导法则求函数的导数时,要分清函数的结构,再利用相应的法则进行求导.
(2)遇到函数的表达式是乘积形式或是商的形式,有时先将函数表达式展开或化简,然后再求导.
练习2 求的导数
(课本P77)例3日常生活中的饮用水通常是经过净化的. 随着水的纯净度的提高,所需净化费用不断增加. 已知将吨水净化到纯净度为时所需费用(单位:元)为
1.求净化到下列纯净度,所需净化费用的瞬时变化率;
(1) (2).
解
所以
(1)因为,所以净化到纯净度为,净化费用的瞬时变化率为元/吨.
(2)因为,所以净化到纯净度为,净化费用的瞬时变化率为21元/吨.
2.根据计算结果能得出哪些结论?
净化到纯净度为时净化费用的变化率是净化到纯净度为时的倍.
即净化到纯净度为98%时净化费用变化的快慢是净化到纯净度为90%时净化费用变化快慢的倍.
这说明水的纯净度越高,需要的净化费用就越多,而且净化费用增加的速度也越快。
(1).
例4 已知函数
(1)求函数的导数
(2)求函数的图象在处的切线方程.
(2)由题意可知切点的横坐标为,
所以切线的斜率是,
切点纵坐标为,
故切点的坐标是,
所以切线方程为,即.
问题5 我们学习了哪些知识内容?
导数的四则运算法则及运用导数的四则运算法则求函数的导数.
追问: 你有什么感受?
运用函数的导数运算法则求函数的导数,比用导数定义求函数的导数要方便很多.
运用导数运算法则可以求很多初等函数的导数,这有助于研究更多函数的性质.
基础题组 课本P78练习123
拔高题组课本P81习题5.2 456
课后作业
再会!
