5.3.2函数的极值与最大(小)值(共23张ppt)
文档属性
| 名称 | 5.3.2函数的极值与最大(小)值(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 20:37:01 | ||
图片预览




文档简介
(共23张PPT)
函数的最大(小)值
------高中数学人教 a 版选择性必修第二册------
第五章 一元函数的导数及其应用
5.3.2函数的极值与最大(小)值
1.了解函数的最大(小)值的概念,能够区分极值与最值;
2.能利用导数求某些函数给定闭区间上不超过三次的多项式的最大(小)值;
3.掌握导数在解决实际问题中的应用。
学习目标
一:情境导入
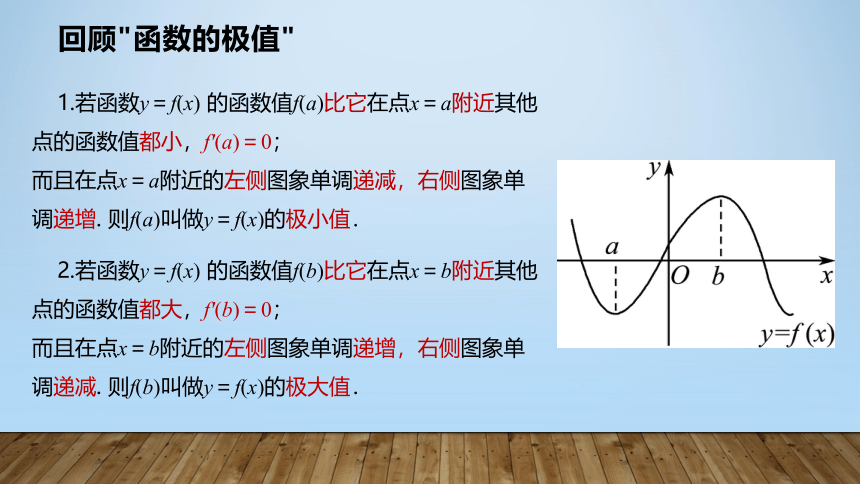
2.若函数y=f(x) 的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;
而且在点x=b附近的左侧图象单调递增,右侧图象单调递减. 则f(b)叫做y=f(x)的极大值.
1.若函数y=f(x) 的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;
而且在点x=a附近的左侧图象单调递减,右侧图象单调递增. 则f(a)叫做y=f(x)的极小值.
回顾"函数的极值"
极值是一个局部概念,只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小. 所以最值问题的学习显得尤为重要。
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高、效益最大等问题,这些问题的解决常常涉及到求一个函数的最大值和最小值问题.
导入”函数的最值”
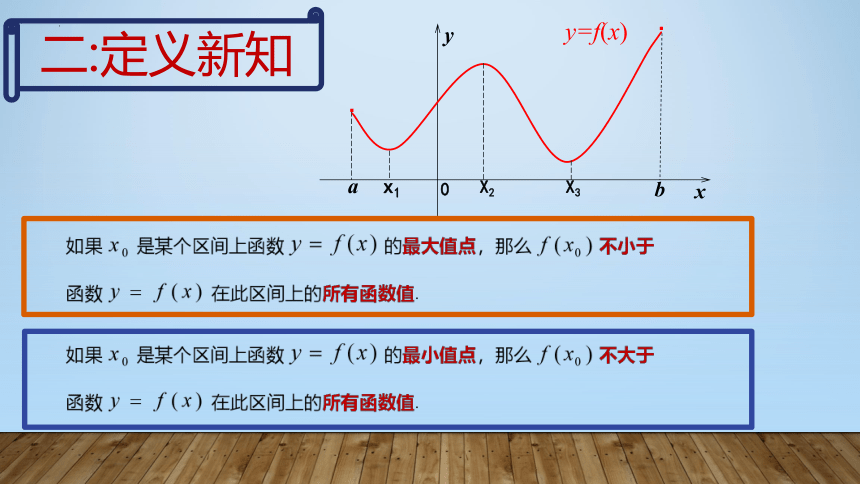
二:定义新知
x
X2
0
a
X3
b
x1
y
y=f(x)
·
·
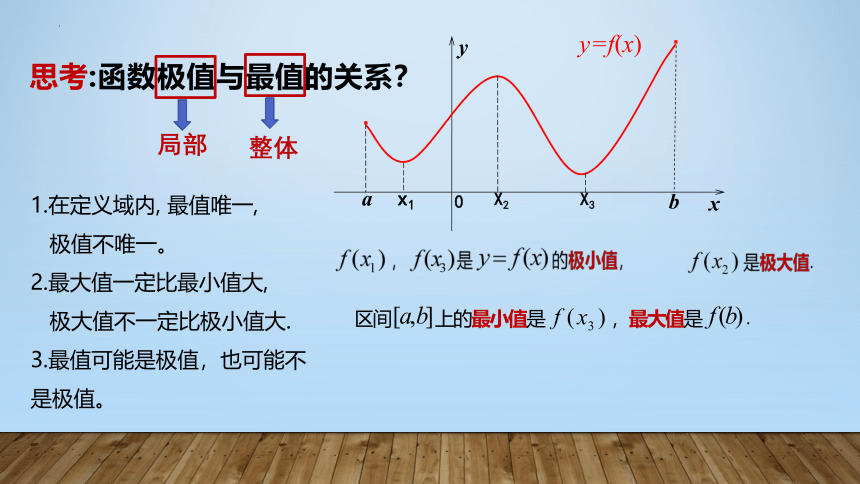
思考:函数极值与最值的关系?
局部
整体
x
X2
0
a
X3
b
x1
y
y=f(x)
·
·
1.在定义域内, 最值唯一,
极值不唯一。
2.最大值一定比最小值大,
极大值不一定比极小值大.
3.最值可能是极值,也可能不是极值。
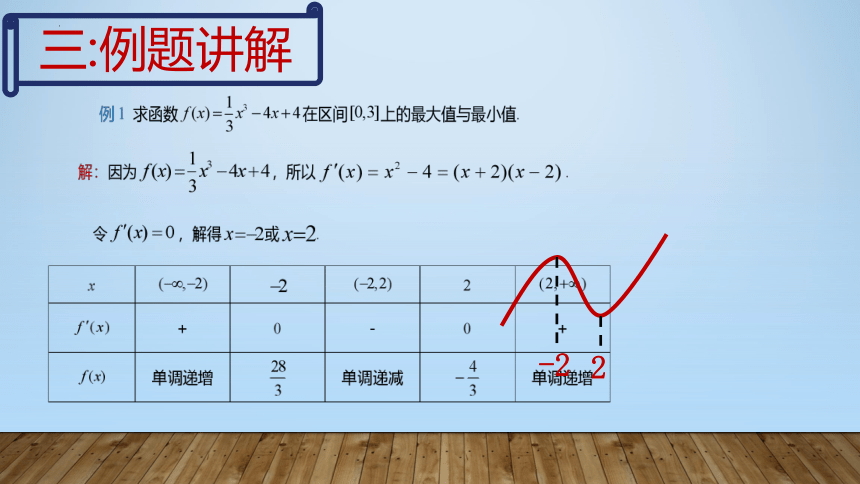
三:例题讲解
-2
2
思考: 求函数最值的方法步骤?
三:例题讲解
正数
-2
A
B
C
1个
2个
1个
0个
思考: 画出函数f(x)的大致图象的步骤有哪些?
四:巩固训练
2
1
五:导数的实际应用
饮料的体积
销售获利
成本
0 2 6
六:课堂小结
0 2 6
3
y=0
六:课堂小结
七:作业布置
教科书习题5.3:第6,8,10题
极值与最值 曲:海伦(桥边姑娘)
求最值,我先求导,找导数的零点。
我找出了那些分区间,我逐一论正负。
导函数为正的区间,原函数在递增;
导函数为负的区间,原函数在递减。
增增减减,你曲折有形,
参照图象,我找出极值。
我说极值与端点值哪个最大?
我把你比一比,大小放心上。
极值与端点值,各显神通。
我把你放心房,最值在荡漾。嗯嗯……
献歌一曲: 极值与最值
谢谢观看!
函数的最大(小)值
------高中数学人教 a 版选择性必修第二册------
第五章 一元函数的导数及其应用
5.3.2函数的极值与最大(小)值
1.了解函数的最大(小)值的概念,能够区分极值与最值;
2.能利用导数求某些函数给定闭区间上不超过三次的多项式的最大(小)值;
3.掌握导数在解决实际问题中的应用。
学习目标
一:情境导入
2.若函数y=f(x) 的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;
而且在点x=b附近的左侧图象单调递增,右侧图象单调递减. 则f(b)叫做y=f(x)的极大值.
1.若函数y=f(x) 的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;
而且在点x=a附近的左侧图象单调递减,右侧图象单调递增. 则f(a)叫做y=f(x)的极小值.
回顾"函数的极值"
极值是一个局部概念,只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小. 所以最值问题的学习显得尤为重要。
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高、效益最大等问题,这些问题的解决常常涉及到求一个函数的最大值和最小值问题.
导入”函数的最值”
二:定义新知
x
X2
0
a
X3
b
x1
y
y=f(x)
·
·
思考:函数极值与最值的关系?
局部
整体
x
X2
0
a
X3
b
x1
y
y=f(x)
·
·
1.在定义域内, 最值唯一,
极值不唯一。
2.最大值一定比最小值大,
极大值不一定比极小值大.
3.最值可能是极值,也可能不是极值。
三:例题讲解
-2
2
思考: 求函数最值的方法步骤?
三:例题讲解
正数
-2
A
B
C
1个
2个
1个
0个
思考: 画出函数f(x)的大致图象的步骤有哪些?
四:巩固训练
2
1
五:导数的实际应用
饮料的体积
销售获利
成本
0 2 6
六:课堂小结
0 2 6
3
y=0
六:课堂小结
七:作业布置
教科书习题5.3:第6,8,10题
极值与最值 曲:海伦(桥边姑娘)
求最值,我先求导,找导数的零点。
我找出了那些分区间,我逐一论正负。
导函数为正的区间,原函数在递增;
导函数为负的区间,原函数在递减。
增增减减,你曲折有形,
参照图象,我找出极值。
我说极值与端点值哪个最大?
我把你比一比,大小放心上。
极值与端点值,各显神通。
我把你放心房,最值在荡漾。嗯嗯……
献歌一曲: 极值与最值
谢谢观看!
