4.4数学归纳法 课件(共26张PPT)
文档属性
| 名称 | 4.4数学归纳法 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 32.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 20:46:51 | ||
图片预览







文档简介
(共26张PPT)
4.4 数学归纳法
情境一
问 题
某人看到树上有几只乌鸦,
深有感触“天下乌鸦一般黑”。
你认为这样的说法可靠吗?为什么?
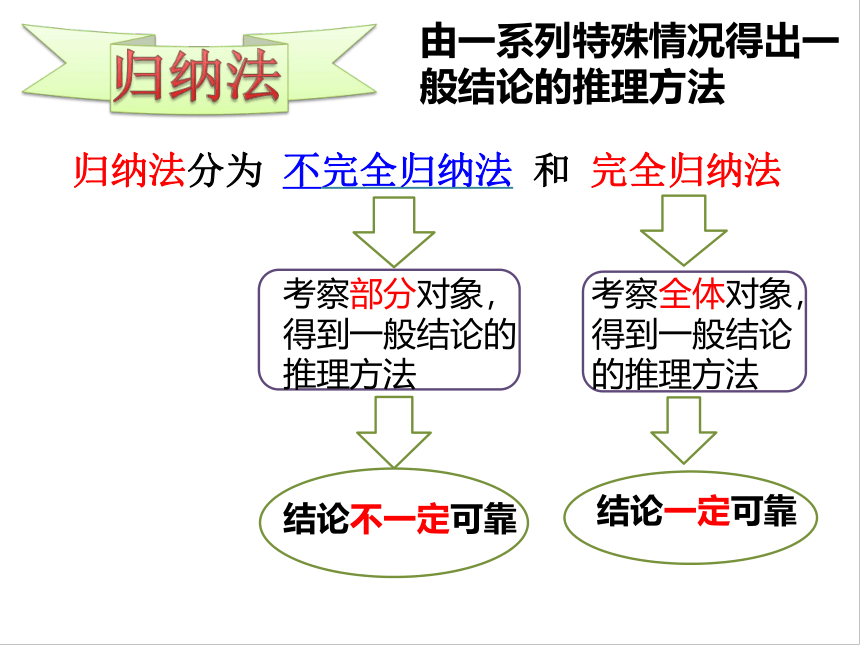
归纳法
归纳法分为 不完全归纳法 和 完全归纳法
考察部分对象,得到一般结论的推理方法
结论不一定可靠
由一系列特殊情况得出一般结论的推理方法
考察全体对象,得到一般结论的推理方法
结论一定可靠
已知数列
满足 , ,
情境二
计算 ,猜想其通项公式并证明。
猜想
如何验证这个猜想呢?
问 题
通过有限个步骤的推理,证明n取所有正整数时命题都成立。
你相信一指之力就能推倒一座摩天大厦吗
探 究
能使多米诺骨牌全部倒下的条件是什么?
多米诺骨牌全部倒下的条件是:
①第一块骨牌必须倒下;
② 任意相邻的两块骨牌,前一块倒下一定导致后一块倒下。
结论
实验一
实验二
小结:第一块骨牌倒下是所有骨牌倒下的基础和前提。
实验三
思 考
你认为条件(2)的作用是什么?如何用数学语言描述?
条件(2)实际上是一个递推关系:
第k块骨牌倒下第k+1块骨牌倒下.
思 考
你认为前面的猜想“数列的通项公式是
与上述多米诺骨牌游戏有相似性吗?
回顾:
一般结构:
递推关系:
是否只要有了上述的递推关系,就能保证 ?
问题:
保证“对于每一个正整数n, ”的条件是:
①
② 递推关系:
结论
骨牌原理 证明 猜想的证明步骤
①第一块骨牌倒下
① 成立
①证明当n=1时,
猜想正确。
②证明“如果前一块倒下,则后一块也跟着倒下”。
②证明“如果
,那么 ”。
②证明“如果n=k时猜想正确,那么n=k+1时,猜想也正确”。
根据①②,所有的骨牌都能倒下。
根据①②,
。
根据①②,猜想对于一切正整数n都成立。
【探究】已知数列 满足 ,
证明:
证:(1)当n=1时,由已知, , ①式成立。
①
(2)假设当 时, ①式成立,即
根据递推公式 ,有
即当 时, ①式也成立。
由(1)(2)可知, ①式对任何 都成立。
由此,我们发现了一个证明与正整数n有关的命题方法,它可按如下两个步骤进行:
(1)证明当n取第一个值
时命题成立;
(2)假设
时命题成立,证明当
时命题也成立。
根据(1)和(2),可知命题对
都成立。
一般地,证明一个与正整数n有关的命题,可按如下步骤进行:
(1)证明当n取第一个值
时命题成立;
(2)“以
时命题成立”为条件,推出“当
时命题也成立”。
根据(1)和(2),可知命题对从 开始的所有正整数都成立。
这种证明方法叫做数学归纳法。
归纳递推
归纳奠基
思 考
数学归纳法中的两个步骤之间有什么关系?
相互依存,缺一不可
【例1】用数学归纳法证明:
如果是一个公差为d的等差数列,那么
对任何都成立。
证:(1)当n=1时,左边= ,右边= ,①式成立。
(2)假设当 时, ①式成立,即
根据等差数列的定义,有
即当 时, ①式也成立。
由(1)(2)可知, ①式对任何 都成立。
①
于是,
【练习1】
试判断 与 的大小。
解:当n=1时,
当n=2时,
当n=3时,
当n=4时,
猜测:
【练习1】
证明猜想
证明:(1)当n=2时, 猜想成立。
(2)假设当n=k时,猜想成立,即
那么
即当 时, 猜想也成立。
由(1)(2)可知, 猜想对任何 都成立。
【注】数学归纳法中的起始值不一定是1.
证明一个与正整数 有关的命题
(1)证明当
时命题成立
对所有正整数 命题都成立。
数学归纳法的结构
(2)假设当 时命题
成立,证明当 时命题也成立。
两个步骤 缺一不可
反思总结 纳入体系
勇攀高峰
数学思想:
归纳思想,递推思想,类比思想
数学方法:
数学归纳法:两步骤 一结论
数学知识:
无限递推转化为有限步验证
实现由量变到质变的飞跃
探究题
“秃子悖论”
情境:一个女孩有茂密的长发。
(1)当n=1,即拔掉第1根头发时,不秃。
(2)若n=k时命题成立,即当拔掉第k根头发时不秃,那么当n=k+1时,也不秃。
由(1)(2)可知,对拔掉任意n根头发,这个女孩都不会变成秃发。
上面的说法正确吗?你能给出一个合理的解释吗?
谢谢大家!
4.4 数学归纳法
情境一
问 题
某人看到树上有几只乌鸦,
深有感触“天下乌鸦一般黑”。
你认为这样的说法可靠吗?为什么?
归纳法
归纳法分为 不完全归纳法 和 完全归纳法
考察部分对象,得到一般结论的推理方法
结论不一定可靠
由一系列特殊情况得出一般结论的推理方法
考察全体对象,得到一般结论的推理方法
结论一定可靠
已知数列
满足 , ,
情境二
计算 ,猜想其通项公式并证明。
猜想
如何验证这个猜想呢?
问 题
通过有限个步骤的推理,证明n取所有正整数时命题都成立。
你相信一指之力就能推倒一座摩天大厦吗
探 究
能使多米诺骨牌全部倒下的条件是什么?
多米诺骨牌全部倒下的条件是:
①第一块骨牌必须倒下;
② 任意相邻的两块骨牌,前一块倒下一定导致后一块倒下。
结论
实验一
实验二
小结:第一块骨牌倒下是所有骨牌倒下的基础和前提。
实验三
思 考
你认为条件(2)的作用是什么?如何用数学语言描述?
条件(2)实际上是一个递推关系:
第k块骨牌倒下第k+1块骨牌倒下.
思 考
你认为前面的猜想“数列的通项公式是
与上述多米诺骨牌游戏有相似性吗?
回顾:
一般结构:
递推关系:
是否只要有了上述的递推关系,就能保证 ?
问题:
保证“对于每一个正整数n, ”的条件是:
①
② 递推关系:
结论
骨牌原理 证明 猜想的证明步骤
①第一块骨牌倒下
① 成立
①证明当n=1时,
猜想正确。
②证明“如果前一块倒下,则后一块也跟着倒下”。
②证明“如果
,那么 ”。
②证明“如果n=k时猜想正确,那么n=k+1时,猜想也正确”。
根据①②,所有的骨牌都能倒下。
根据①②,
。
根据①②,猜想对于一切正整数n都成立。
【探究】已知数列 满足 ,
证明:
证:(1)当n=1时,由已知, , ①式成立。
①
(2)假设当 时, ①式成立,即
根据递推公式 ,有
即当 时, ①式也成立。
由(1)(2)可知, ①式对任何 都成立。
由此,我们发现了一个证明与正整数n有关的命题方法,它可按如下两个步骤进行:
(1)证明当n取第一个值
时命题成立;
(2)假设
时命题成立,证明当
时命题也成立。
根据(1)和(2),可知命题对
都成立。
一般地,证明一个与正整数n有关的命题,可按如下步骤进行:
(1)证明当n取第一个值
时命题成立;
(2)“以
时命题成立”为条件,推出“当
时命题也成立”。
根据(1)和(2),可知命题对从 开始的所有正整数都成立。
这种证明方法叫做数学归纳法。
归纳递推
归纳奠基
思 考
数学归纳法中的两个步骤之间有什么关系?
相互依存,缺一不可
【例1】用数学归纳法证明:
如果是一个公差为d的等差数列,那么
对任何都成立。
证:(1)当n=1时,左边= ,右边= ,①式成立。
(2)假设当 时, ①式成立,即
根据等差数列的定义,有
即当 时, ①式也成立。
由(1)(2)可知, ①式对任何 都成立。
①
于是,
【练习1】
试判断 与 的大小。
解:当n=1时,
当n=2时,
当n=3时,
当n=4时,
猜测:
【练习1】
证明猜想
证明:(1)当n=2时, 猜想成立。
(2)假设当n=k时,猜想成立,即
那么
即当 时, 猜想也成立。
由(1)(2)可知, 猜想对任何 都成立。
【注】数学归纳法中的起始值不一定是1.
证明一个与正整数 有关的命题
(1)证明当
时命题成立
对所有正整数 命题都成立。
数学归纳法的结构
(2)假设当 时命题
成立,证明当 时命题也成立。
两个步骤 缺一不可
反思总结 纳入体系
勇攀高峰
数学思想:
归纳思想,递推思想,类比思想
数学方法:
数学归纳法:两步骤 一结论
数学知识:
无限递推转化为有限步验证
实现由量变到质变的飞跃
探究题
“秃子悖论”
情境:一个女孩有茂密的长发。
(1)当n=1,即拔掉第1根头发时,不秃。
(2)若n=k时命题成立,即当拔掉第k根头发时不秃,那么当n=k+1时,也不秃。
由(1)(2)可知,对拔掉任意n根头发,这个女孩都不会变成秃发。
上面的说法正确吗?你能给出一个合理的解释吗?
谢谢大家!
