青岛版八年级数学下册 6.1 平行四边形及其性质(1) 课件
文档属性
| 名称 | 青岛版八年级数学下册 6.1 平行四边形及其性质(1) 课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 336.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-27 10:09:34 | ||
图片预览

文档简介
(共12张PPT)
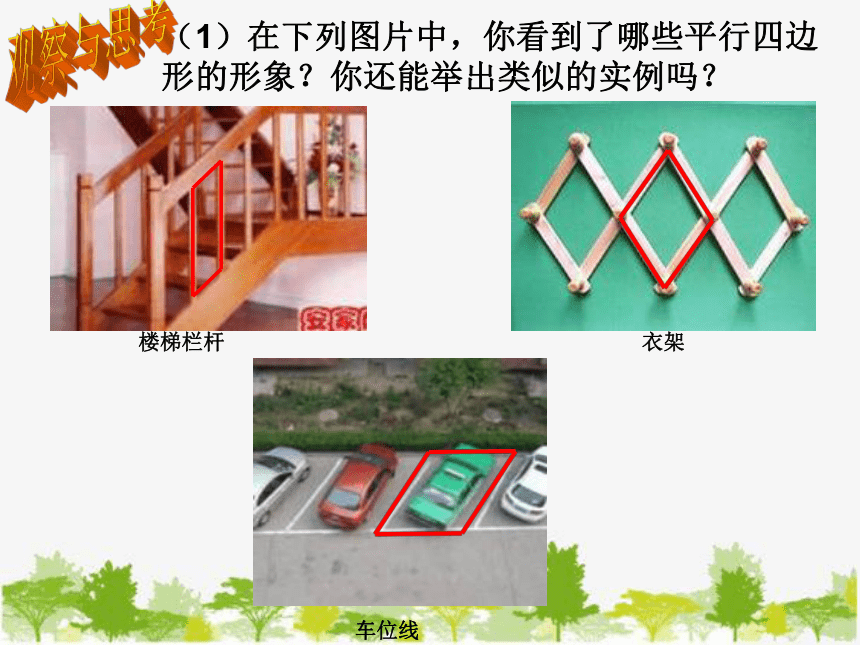
楼梯栏杆
衣架
车位线
(1)在下列图片中,你看到了哪些平行四边形的形象?你还能举出类似的实例吗?
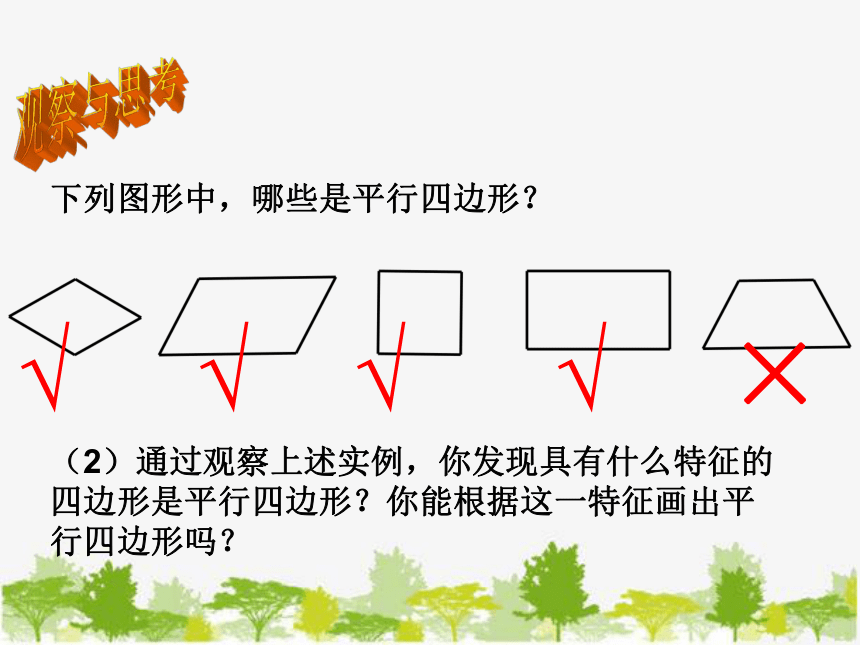
下列图形中,哪些是平行四边形?
(2)通过观察上述实例,你发现具有什么特征的四边形是平行四边形?你能根据这一特征画出平行四边形吗?
√
×
√
√
√
A
D
C
B
记作:
读作:平行四边形ABCD
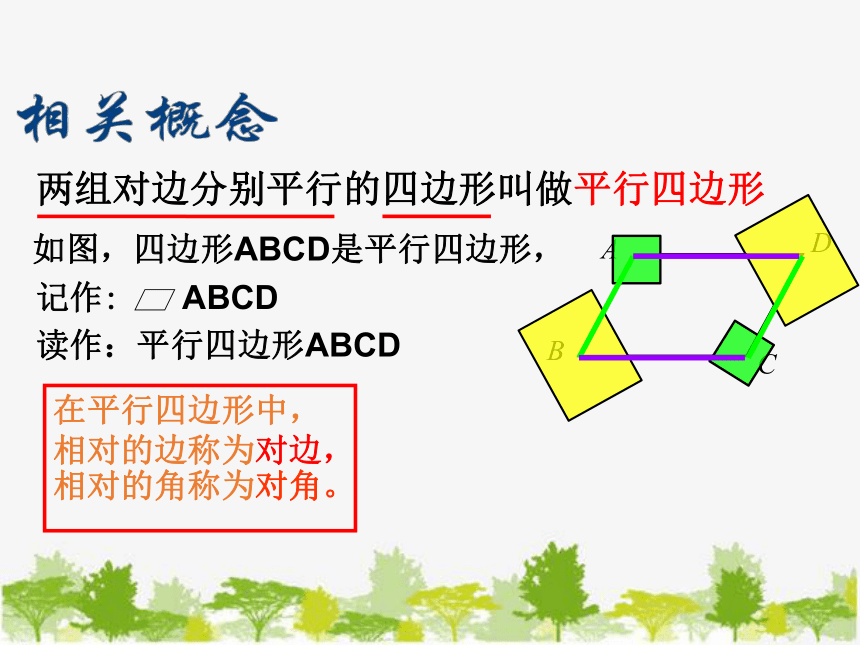
两组对边分别平行的四边形叫做平行四边形
如图,四边形ABCD是平行四边形,
在平行四边形中,
相对的边称为对边,
相对的角称为对角。
ABCD
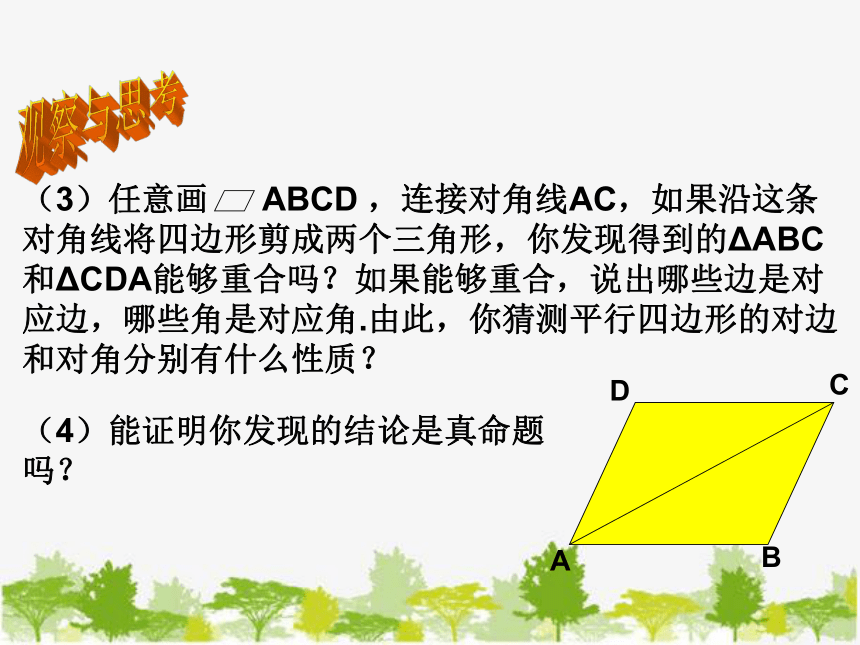
(3)任意画 ,连接对角线AC,如果沿这条对角线将四边形剪成两个三角形,你发现得到的ΔABC和ΔCDA能够重合吗?如果能够重合,说出哪些边是对应边,哪些角是对应角.由此,你猜测平行四边形的对边和对角分别有什么性质?
ABCD
D
A
C
B
(4)能证明你发现的结论是真命题吗?
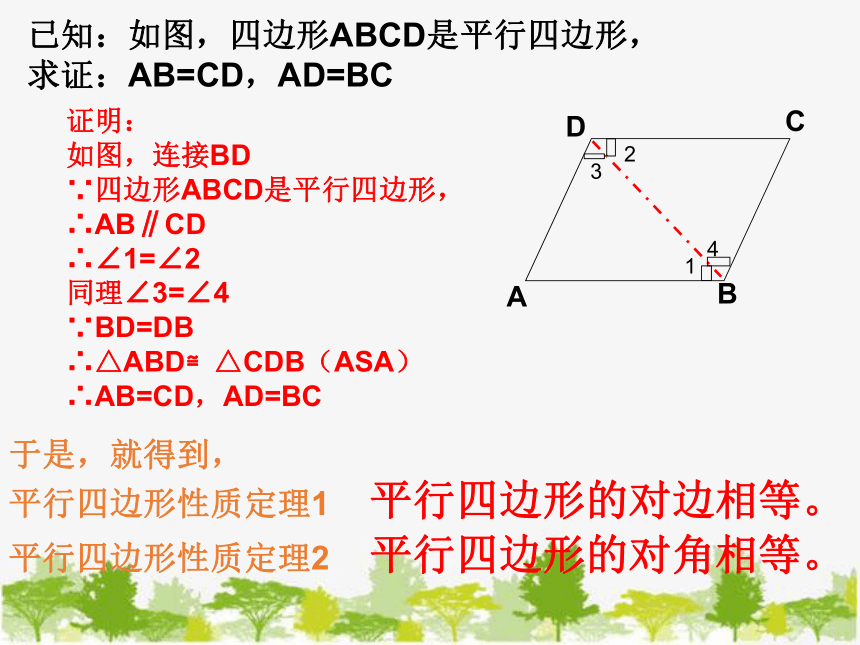
已知:如图,四边形ABCD是平行四边形,
求证:AB=CD,AD=BC
D
A
C
B
4
3
2
1
证明:
如图,连接BD
∵四边形ABCD是平行四边形,
∴AB∥CD
∴∠1=∠2
同理∠3=∠4
∵BD=DB
∴△ABD≌△CDB(ASA)
∴AB=CD,AD=BC
于是,就得到,
平行四边形性质定理1 平行四边形的对边相等。
平行四边形性质定理2 平行四边形的对角相等。
例1 求证:
(1)夹在两条平行线间的平行线段相等;
(2)如果两条直线平行,那么一条直线上各点到另一条直线上的距离相等.
(1)已知:如图,l1‖l2 ,A,D是直线l1 上的任意两点,过点A,D作AB‖CD,分别交l2 于点B,C.求证:AB=CD.
证明:∵AD‖BC,AB‖CD,
∴四边形ABCD是平行四边形(平行四边形定义),
∴AB=CD(平行四边形行的性质定理1).
(2)已知:如图, l1‖l2 ,A,D是直线l1 上的任意两点,AB⊥l2 ,垂足是B,CD⊥l2 ,垂足是C.求证:AB=CD.
证明: ∵ AB⊥l2 , CD⊥l2 ,
∴∠ABC=90 ,∠DCB=90 .
∴∠ABC=90 +∠DCB=180
∴AB‖CD
由(1)可知AB=CD.
例2 如图,在 中,∠A=36°,
求其他各个内角的度数。
ABCD
D
A
C
B
解:
∵四边形ABCD是平行四边形,
∴∠C=∠A=36°
∵AD∥BC
∴∠B=180°-∠A=180 °-36°=144°
∴∠D=∠B=144°
1.填空:
(1)平行四边形___平行,___相等,___相等;
(2)如下图平行四边形ABCD中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.
对边
对边
对角
A
O
H
F
E
D
C
B
G
9
巩固练习
2、如图,已知在平行四边形ABCD中,AB=4 cm,AD=7 cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
解:
1
2
∵四边形ABCD是平行四边形,
∴AB∥CF
∴∠1=∠F
又∵AD平分∠ABC
∴∠1=∠2
∴∠F=∠2
∴CB=CF
∵AB=4cm,AD=7cm
∴CD=AB=4cm,CF=CB=AD=7cm
∴DF=CF-CD=3cm
如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于F,∠ADC的平分线DG交AB于G.
求证:AF=GB;
变式练习:
分析:
AB∥CD
DG平分∠ADC
AB∥CD
CF平分∠BCD
AD=AG
BC=BF
平行四边形ABCD
AD=BC
AG=BF
AF=GB
P6
练习 1、2
楼梯栏杆
衣架
车位线
(1)在下列图片中,你看到了哪些平行四边形的形象?你还能举出类似的实例吗?
下列图形中,哪些是平行四边形?
(2)通过观察上述实例,你发现具有什么特征的四边形是平行四边形?你能根据这一特征画出平行四边形吗?
√
×
√
√
√
A
D
C
B
记作:
读作:平行四边形ABCD
两组对边分别平行的四边形叫做平行四边形
如图,四边形ABCD是平行四边形,
在平行四边形中,
相对的边称为对边,
相对的角称为对角。
ABCD
(3)任意画 ,连接对角线AC,如果沿这条对角线将四边形剪成两个三角形,你发现得到的ΔABC和ΔCDA能够重合吗?如果能够重合,说出哪些边是对应边,哪些角是对应角.由此,你猜测平行四边形的对边和对角分别有什么性质?
ABCD
D
A
C
B
(4)能证明你发现的结论是真命题吗?
已知:如图,四边形ABCD是平行四边形,
求证:AB=CD,AD=BC
D
A
C
B
4
3
2
1
证明:
如图,连接BD
∵四边形ABCD是平行四边形,
∴AB∥CD
∴∠1=∠2
同理∠3=∠4
∵BD=DB
∴△ABD≌△CDB(ASA)
∴AB=CD,AD=BC
于是,就得到,
平行四边形性质定理1 平行四边形的对边相等。
平行四边形性质定理2 平行四边形的对角相等。
例1 求证:
(1)夹在两条平行线间的平行线段相等;
(2)如果两条直线平行,那么一条直线上各点到另一条直线上的距离相等.
(1)已知:如图,l1‖l2 ,A,D是直线l1 上的任意两点,过点A,D作AB‖CD,分别交l2 于点B,C.求证:AB=CD.
证明:∵AD‖BC,AB‖CD,
∴四边形ABCD是平行四边形(平行四边形定义),
∴AB=CD(平行四边形行的性质定理1).
(2)已知:如图, l1‖l2 ,A,D是直线l1 上的任意两点,AB⊥l2 ,垂足是B,CD⊥l2 ,垂足是C.求证:AB=CD.
证明: ∵ AB⊥l2 , CD⊥l2 ,
∴∠ABC=90 ,∠DCB=90 .
∴∠ABC=90 +∠DCB=180
∴AB‖CD
由(1)可知AB=CD.
例2 如图,在 中,∠A=36°,
求其他各个内角的度数。
ABCD
D
A
C
B
解:
∵四边形ABCD是平行四边形,
∴∠C=∠A=36°
∵AD∥BC
∴∠B=180°-∠A=180 °-36°=144°
∴∠D=∠B=144°
1.填空:
(1)平行四边形___平行,___相等,___相等;
(2)如下图平行四边形ABCD中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.
对边
对边
对角
A
O
H
F
E
D
C
B
G
9
巩固练习
2、如图,已知在平行四边形ABCD中,AB=4 cm,AD=7 cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
解:
1
2
∵四边形ABCD是平行四边形,
∴AB∥CF
∴∠1=∠F
又∵AD平分∠ABC
∴∠1=∠2
∴∠F=∠2
∴CB=CF
∵AB=4cm,AD=7cm
∴CD=AB=4cm,CF=CB=AD=7cm
∴DF=CF-CD=3cm
如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于F,∠ADC的平分线DG交AB于G.
求证:AF=GB;
变式练习:
分析:
AB∥CD
DG平分∠ADC
AB∥CD
CF平分∠BCD
AD=AG
BC=BF
平行四边形ABCD
AD=BC
AG=BF
AF=GB
P6
练习 1、2
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
