2.3气体的等容变化和等压变化(共20张ppt)
文档属性
| 名称 | 2.3气体的等容变化和等压变化(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 25.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-25 22:02:31 | ||
图片预览






文档简介
(共20张PPT)
2.3气体的等容变化
和等压变化
0
p/V
T
A
B
273.15
1.掌握查理定律和盖—吕萨克定律的内容、表达式及适用条件.
2.理解p-T图象与V-T图象的物理意义.
3.熟练掌握查理定律和盖—吕萨克定律,并能灵活运用其解决实际问题.
学习目标
前情回顾
一、气体的状态参量:P、V、T
二、玻意耳定律: PV=C P1V1=P2V2
三、等温变化的图像:
p
1/V
p
V
一、气体的等容变化
一定质量的气体,在体积不变的条件下其压强与温度变化的关系,叫做气体的等容变化。
体积不变时,气体的压强和温度之间有什么关系?
正 比?
想一想:
问题:一定质量的气体,在体积不变的条件下其压强与温度变化的关系
注射器内一定质量的气体.
压强
温度
将注射器浸在水中,通过改变水
的温度从而改变注射器内气体温度
1、如何选取研究对象?
2、如何测量需要的物理量?
3、怎样改变气体的温度?
用压强传感器测量
用温度传感器测量
0
p
t/0C
A
B
甲
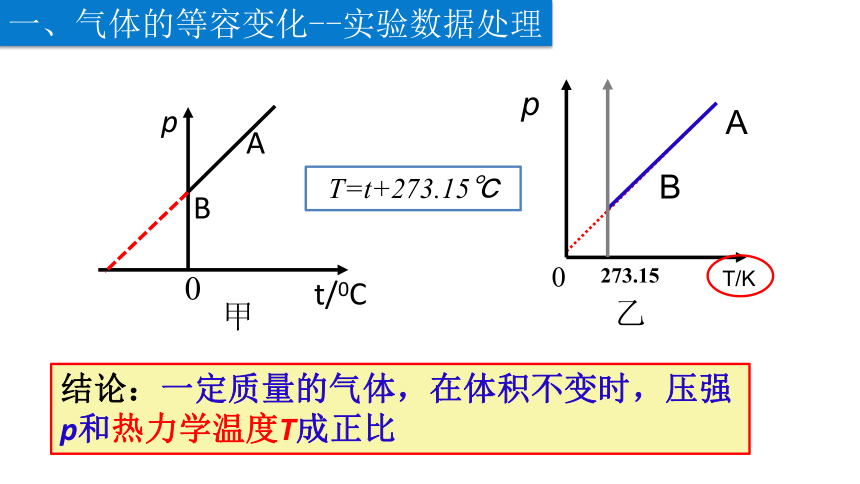
一、气体的等容变化--实验数据处理
结论:一定质量的气体,在体积不变时,压强p和热力学温度T成正比
0
乙
p
T/K
A
B
273.15
T=t+273.15℃
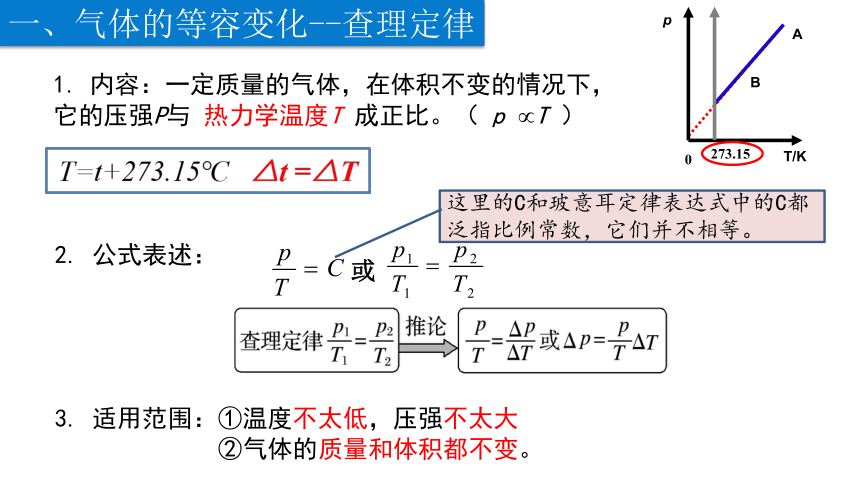
内容:一定质量的气体,在体积不变的情况下,
它的压强P与 热力学温度T 成正比。( p T )
或
2. 公式表述:
这里的C和玻意耳定律表达式中的C都泛指比例常数,它们并不相等。
3. 适用范围:①温度不太低,压强不太大
②气体的质量和体积都不变。
一、气体的等容变化--查理定律
T=t+273.15℃
0
p
T/K
A
B
273.15
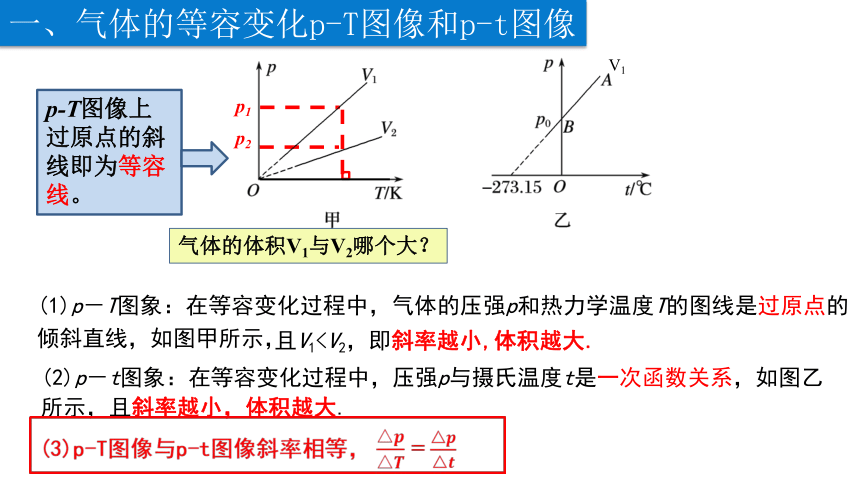
(1)p-T图象:在等容变化过程中,气体的压强p和热力学温度T的图线是过原点的倾斜直线,如图甲所示,
(2)p-t图象:在等容变化过程中,压强p与摄氏温度t是一次函数关系,如图乙所示,且斜率越小,体积越大.
p-T图像上过原点的斜线即为等容线。
且V1气体的体积V1与V2哪个大?
(3)p-T图像与p-t图像斜率相等, =
一、气体的等容变化p-T图像和p-t图像
V1
p1
p2
如图 ,某种气体在状态 A 时压强为 2×105 Pa,体积为 1 m3,温度为200 K。
(1) 它在等温过程中由状态 A 变为状态 B,状态 B 的体积为 2 m3。求状态 B 的压强。(2) 随后,又由状态 B 在等容过程中变为状态 C,状态 C 的温度为 300 K。求状态 C 的压强。
【例1】
解(1)气体由状态A变为状态B的过程遵从玻意耳定律。由 pAVA=pBVB得状态B的压强
PB = = Pa = 105Pa
(2)气体由状态B变为状态C的过程遵从查理定律。
由 =得状态C的压强
PC = = Pa = 1.5×105Pa
【练一练】
在标准大气压下对B管进行温度标度(1标准大气压相当于76 cm水银柱的压强).已知当温度t=27 ℃时的刻度线在x=16 cm处,问t=0 ℃的刻度线在x为多少厘米处?
有人设计了一种测温装置,其结构如图所示.玻璃泡A内封有一定量气体,与A相连的B管插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出.设B管的体积与A泡的体积相比可略去不计.
E
F
由查理定律:=得:p2=54.6 cmHg
所以t=0 ℃时水银面高度,即刻度线的位置是:
x0=(76-54.6)cm=21.4 cm.
一定质量的气体,在体积不变的情况下,温度由0 ℃升高到10 ℃时,其压强的增加量为Δp1,当它由100 ℃升高到110 ℃时,其压强的增加量为Δp2,则Δp1与Δp2之比是( )
A.10∶1 B.373∶273
C.1∶1 D.383∶283
C
【练一练】
二、气体的等压变化
一定质量的气体,在压强不变的条件下其体积与温度变化的关系,叫做气体的等压变化。
气体受热膨胀——温度升高,体积增大
正 相关
内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比.
或
2. 公式表述:
3. 适用范围:①温度不太低,压强不太大
②气体的质量和压强都不变。
这里的C和玻意耳定律查理定律表达式中的C都泛指比例常数,它们并不相等。
二、气体的等压变化—盖-吕萨克定律
0
V
T/K
A
B
273.15
T=t+273.15℃
(2)V-t图象:在等压变化过程中,体积V与摄氏温度t是一次函数关系,如图乙所示,且斜率越小,压强越大。
(1)V-T图象:在等压变化过程中,气体的体积V随热力学温度T变化的图线是过原点的倾斜直线,如图甲所示,
V-T图像上过原点的斜线即为等压线。
且p1二、气体的等压变化:V-T图像和V-t图像
(3)V-T图像与V-t图像斜率相等, =
p1
V1
V2
【例2】如图所 示,上端开口的光滑圆柱形汽缸竖直放置,截面积为40 cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内.在汽缸内距缸底60 cm处设有a、b两限制装置,使活塞只能向上滑动.开始时活塞搁在a、b上,缸内气体的压强为p0(p0=1.0×105 Pa为大气压强),温度为300 K.现缓慢加热汽缸内气体,当温度为330 K,活塞恰好离开a、b;当温度为360 K时,活塞上升了4 cm.
g取10 m/s2 求:(1)活塞的质量; (2)物体A的体积.
1、确定研究对象,即被封闭的气体.
2、分析研究对象在状态变化时是否:质量一定,体积/压强不变.
3、确定初、末两个状态的压强/体积、温度(不是热力学温度先转化为热力学温度).
4、根据查理定律/盖-吕萨克定律列式求解.
利用查理定律和盖-吕萨克定律的解题思路
不 同 点 图象
纵坐标 压强p 体积V
斜线意义 同一条线上,体积相等 同一条线上,压强相等
相同点 ①都是一条通过原点的倾斜直线 ②横坐标都是热力学温度T ③都是斜率越大,气体的另外一个状态参量越小
三、p-T图像和V-T图像比较
【例3】.如图甲所示是一定质量的气体由状态A经过状态B变为状态C的V-T图象。已知气体在状态A时的压强是1.5×105 Pa。
(1)说出A→B过程中压强变化的情形,并根据图象提供的信息,计算图中TA的温度值。
(2)请在图乙坐标系中,画出由状态A经过状态B变为状态C的p-T的图象,并在图线相应位置上标出字母A、B、C。
A
B
C
(1)A→B为等压过程,
VA=0.4m3VB=0.6m3
TA=? TB=300K
= 解得:TA=200K
(2)B→C为等容过程,
pB=1.5×105Pa pC=
TB=300K TC=300K = 解得:pC=2×105Pa
内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比.
或
2. 数学表达式:
二、气体的等压变化—盖-吕萨克定律
0
V
T/K
A
B
273.15
内容:一定质量的气体,在体积不变的情况下,
它的压强P与 热力学温度T成正比。
一、气体的等容变化--查理定律
0
p
T/K
A
B
273.15
或
2. 数学表达式:
小结
感谢聆听!
2.3气体的等容变化
和等压变化
0
p/V
T
A
B
273.15
1.掌握查理定律和盖—吕萨克定律的内容、表达式及适用条件.
2.理解p-T图象与V-T图象的物理意义.
3.熟练掌握查理定律和盖—吕萨克定律,并能灵活运用其解决实际问题.
学习目标
前情回顾
一、气体的状态参量:P、V、T
二、玻意耳定律: PV=C P1V1=P2V2
三、等温变化的图像:
p
1/V
p
V
一、气体的等容变化
一定质量的气体,在体积不变的条件下其压强与温度变化的关系,叫做气体的等容变化。
体积不变时,气体的压强和温度之间有什么关系?
正 比?
想一想:
问题:一定质量的气体,在体积不变的条件下其压强与温度变化的关系
注射器内一定质量的气体.
压强
温度
将注射器浸在水中,通过改变水
的温度从而改变注射器内气体温度
1、如何选取研究对象?
2、如何测量需要的物理量?
3、怎样改变气体的温度?
用压强传感器测量
用温度传感器测量
0
p
t/0C
A
B
甲
一、气体的等容变化--实验数据处理
结论:一定质量的气体,在体积不变时,压强p和热力学温度T成正比
0
乙
p
T/K
A
B
273.15
T=t+273.15℃
内容:一定质量的气体,在体积不变的情况下,
它的压强P与 热力学温度T 成正比。( p T )
或
2. 公式表述:
这里的C和玻意耳定律表达式中的C都泛指比例常数,它们并不相等。
3. 适用范围:①温度不太低,压强不太大
②气体的质量和体积都不变。
一、气体的等容变化--查理定律
T=t+273.15℃
0
p
T/K
A
B
273.15
(1)p-T图象:在等容变化过程中,气体的压强p和热力学温度T的图线是过原点的倾斜直线,如图甲所示,
(2)p-t图象:在等容变化过程中,压强p与摄氏温度t是一次函数关系,如图乙所示,且斜率越小,体积越大.
p-T图像上过原点的斜线即为等容线。
且V1
(3)p-T图像与p-t图像斜率相等, =
一、气体的等容变化p-T图像和p-t图像
V1
p1
p2
如图 ,某种气体在状态 A 时压强为 2×105 Pa,体积为 1 m3,温度为200 K。
(1) 它在等温过程中由状态 A 变为状态 B,状态 B 的体积为 2 m3。求状态 B 的压强。(2) 随后,又由状态 B 在等容过程中变为状态 C,状态 C 的温度为 300 K。求状态 C 的压强。
【例1】
解(1)气体由状态A变为状态B的过程遵从玻意耳定律。由 pAVA=pBVB得状态B的压强
PB = = Pa = 105Pa
(2)气体由状态B变为状态C的过程遵从查理定律。
由 =得状态C的压强
PC = = Pa = 1.5×105Pa
【练一练】
在标准大气压下对B管进行温度标度(1标准大气压相当于76 cm水银柱的压强).已知当温度t=27 ℃时的刻度线在x=16 cm处,问t=0 ℃的刻度线在x为多少厘米处?
有人设计了一种测温装置,其结构如图所示.玻璃泡A内封有一定量气体,与A相连的B管插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出.设B管的体积与A泡的体积相比可略去不计.
E
F
由查理定律:=得:p2=54.6 cmHg
所以t=0 ℃时水银面高度,即刻度线的位置是:
x0=(76-54.6)cm=21.4 cm.
一定质量的气体,在体积不变的情况下,温度由0 ℃升高到10 ℃时,其压强的增加量为Δp1,当它由100 ℃升高到110 ℃时,其压强的增加量为Δp2,则Δp1与Δp2之比是( )
A.10∶1 B.373∶273
C.1∶1 D.383∶283
C
【练一练】
二、气体的等压变化
一定质量的气体,在压强不变的条件下其体积与温度变化的关系,叫做气体的等压变化。
气体受热膨胀——温度升高,体积增大
正 相关
内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比.
或
2. 公式表述:
3. 适用范围:①温度不太低,压强不太大
②气体的质量和压强都不变。
这里的C和玻意耳定律查理定律表达式中的C都泛指比例常数,它们并不相等。
二、气体的等压变化—盖-吕萨克定律
0
V
T/K
A
B
273.15
T=t+273.15℃
(2)V-t图象:在等压变化过程中,体积V与摄氏温度t是一次函数关系,如图乙所示,且斜率越小,压强越大。
(1)V-T图象:在等压变化过程中,气体的体积V随热力学温度T变化的图线是过原点的倾斜直线,如图甲所示,
V-T图像上过原点的斜线即为等压线。
且p1
(3)V-T图像与V-t图像斜率相等, =
p1
V1
V2
【例2】如图所 示,上端开口的光滑圆柱形汽缸竖直放置,截面积为40 cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内.在汽缸内距缸底60 cm处设有a、b两限制装置,使活塞只能向上滑动.开始时活塞搁在a、b上,缸内气体的压强为p0(p0=1.0×105 Pa为大气压强),温度为300 K.现缓慢加热汽缸内气体,当温度为330 K,活塞恰好离开a、b;当温度为360 K时,活塞上升了4 cm.
g取10 m/s2 求:(1)活塞的质量; (2)物体A的体积.
1、确定研究对象,即被封闭的气体.
2、分析研究对象在状态变化时是否:质量一定,体积/压强不变.
3、确定初、末两个状态的压强/体积、温度(不是热力学温度先转化为热力学温度).
4、根据查理定律/盖-吕萨克定律列式求解.
利用查理定律和盖-吕萨克定律的解题思路
不 同 点 图象
纵坐标 压强p 体积V
斜线意义 同一条线上,体积相等 同一条线上,压强相等
相同点 ①都是一条通过原点的倾斜直线 ②横坐标都是热力学温度T ③都是斜率越大,气体的另外一个状态参量越小
三、p-T图像和V-T图像比较
【例3】.如图甲所示是一定质量的气体由状态A经过状态B变为状态C的V-T图象。已知气体在状态A时的压强是1.5×105 Pa。
(1)说出A→B过程中压强变化的情形,并根据图象提供的信息,计算图中TA的温度值。
(2)请在图乙坐标系中,画出由状态A经过状态B变为状态C的p-T的图象,并在图线相应位置上标出字母A、B、C。
A
B
C
(1)A→B为等压过程,
VA=0.4m3VB=0.6m3
TA=? TB=300K
= 解得:TA=200K
(2)B→C为等容过程,
pB=1.5×105Pa pC=
TB=300K TC=300K = 解得:pC=2×105Pa
内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比.
或
2. 数学表达式:
二、气体的等压变化—盖-吕萨克定律
0
V
T/K
A
B
273.15
内容:一定质量的气体,在体积不变的情况下,
它的压强P与 热力学温度T成正比。
一、气体的等容变化--查理定律
0
p
T/K
A
B
273.15
或
2. 数学表达式:
小结
感谢聆听!
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
