5.2.2递归课件-2021-2022学年浙教版(2019)高中信息技术选修1(16PPT)
文档属性
| 名称 | 5.2.2递归课件-2021-2022学年浙教版(2019)高中信息技术选修1(16PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 644.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-04-26 07:19:26 | ||
图片预览




文档简介
(共16张PPT)
5.2.2 递归
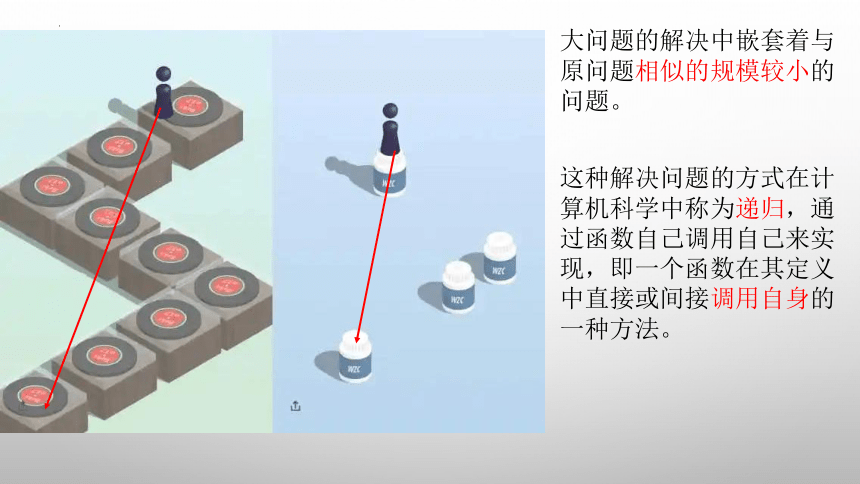
大问题的解决中嵌套着与
原问题相似的规模较小的
问题。
这种解决问题的方式在计
算机科学中称为递归,通
过函数自己调用自己来实
现,即一个函数在其定义
中直接或间接调用自身的
一种方法。
在数据结构与算法设计中,递归十分有用,它往往能使函数的定义和算法
的描述简洁且易于理解,极大地减少程序代码量。如前面学过的的二叉树,
由于其本身固有的递归特性,特别适合用递归的形式来描述。
能采用递归描述的算法通常有这样的特征:为求解规模为N的问题,设法将
它分解成规模较小的问题,然后从这些小问题的解中方便地构造出大问题的
解,并且这些规模较小的问题也能采用同样的分解和综合方法。
当递归到达某个边界,如问题规模缩减为0或1时,能直接得解。因此,在设
计递归算法时,要满足两个条件:确定递归公式和递归结束条件。
例:利用递归算法求n的阶乘(n!=1*2*…*n)。由数学知识可知,n阶乘
的递归定义为:它等于n乘以n-1的阶乘,即n!=n*(n-1)!,并且规定0!=1。
设函数fac(n)=n!,则fac(n)可表示为:
fac(n)=
1
(n=0)
n*fac(n-1) (n>0)
按照这个公式,可以将求n!的问题转化成求(n-1)!的问题;而求(n-1)!的问题,
又可以转化成求(n-2)!的问题;求(n-2)!的问题,又可以转化成求(n-3)!的
问题,如此继续,直到最后转化成求0!的问题。再反过来,依次求出1!,
2!,…,直到最后求出n!。因此,在该问题中,递归公式是
fac(n)=n*fac(n-1),当n=0时递归结束。
求n的阶乘的相应的程序及测试结果如下:
def fac(n):
if n==0:
s=1
else:
s=n*fac(n-1)
return s
print(fac(3))
当主程序执行函数fac(3)时,引起第1次函数调用,进入函数后,
参数n=3,应执行计算3*fac(2)。直到计算fac(0),将引起对函数fac的
第4次调用。
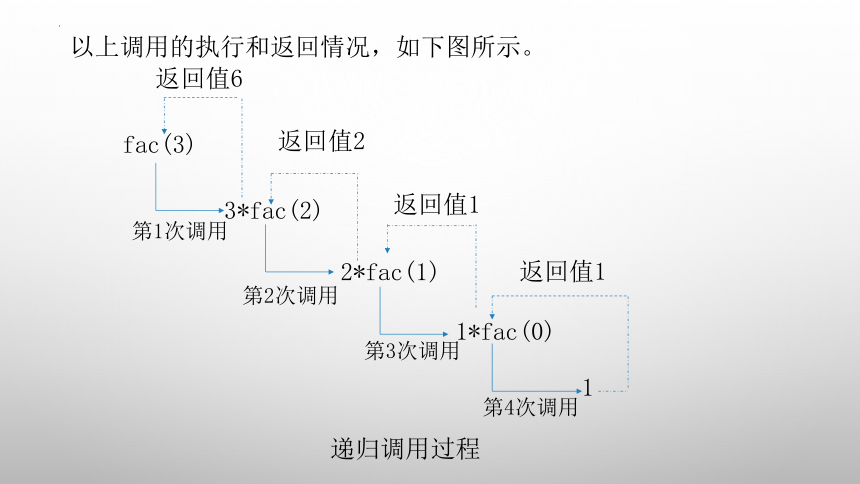
以上调用的执行和返回情况,如下图所示。
fac(3)
3*fac(2)
第1次调用
第2次调用
2*fac(1)
第3次调用
1*fac(0)
第4次调用
1
递归调用过程
返回值1
返回值1
返回值2
返回值6
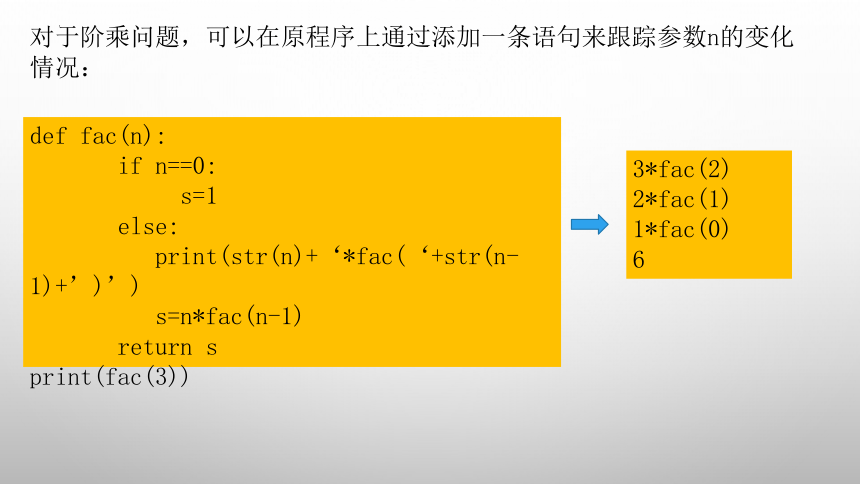
对于阶乘问题,可以在原程序上通过添加一条语句来跟踪参数n的变化
情况:
def fac(n):
if n==0:
s=1
else:
print(str(n)+‘*fac(‘+str(n-1)+’)’)
s=n*fac(n-1)
return s
print(fac(3))
3*fac(2)
2*fac(1)
1*fac(0)
6
利用迭代和递归思想解决问题时有何区别?算法实现时两者有哪些优缺点?
迭代的思想,是一种由旧值不断推出新值的过程。它包括三个方面:
一、确定迭代变量;二、建立迭代关系式;三、控制迭代过程,使
程序能够停止下来。
递归思想,是一种把数据规模较大、较复杂的问题分解成规模较小的问题,
进而构造出整个问题解的思想方法。递归算法的执行过程分递推和回归两
个阶段,其中的关键是如何建立递归关系式与控制程序停止。
一般而言,迭代思想实现的难点在于建立正确的迭代公式,通常要借助
循环语句。而递归思想比较难以理解,程序编写简洁,但递归程序的效率
相对不高。
练习:
1.验证角谷猜想。所谓角谷猜想,是指对于任意一个正整数,若是奇数,
则乘3加1;若是偶数,则除以2。得到的结果再按照上述规则重复处理,
最终总能够得到1。
要求:编写一个程序,输入一个正整数n,把n经过有限次运算后,输出最终变成1的
全过程。
a=int(input(“请输入一个正整数:”))
while a!=1:
print(a)
if a%2==1:
a=a*3+1
else:
a=a//2
print(a)
请输入一个正整数:21
21
64
32
16
8
4
2
1
2.斐波那契数列是这样一个数列:1,1,2,3,5,8,13,21,34,…,其定义如下:
f(0)=0
f(1)=1
f(n)=f(n-1)+f(n-2)(n>=2)
编程求f(40)的值,请分别用迭代和递归算法实现,并分析这两种算法的时间
复杂度。
迭代程序 递归程序
f0=0 f1=1 n=2 while n<=40: f=f1+f0 f0=f1 f1=f n=n+1 print(f1) def fib(n):
if n<1:
return 0
elif n==1:
return 1
else:
return fib(n-1)+fib(n-2)
print(fib(40))
利用迭代算法求斐波那契数列,从n>=2开始计算,用f0和f1两个数相加
求出结果,重复执行n-1次即可,算法的时间复杂度与n成正比,即算法
的时间复杂度为O(n)。
利用递归算法求斐波那契数列,要求解fib(n),必须先计算fib(n-1)和
fib(n-2),计算fib(n-1)和fib(n-2),又必须先计算fib(n-3)和fib(n-4)……
以此类推,直至计算到fib(1)和fib(0),然后回归得到fib(n-1)和fib(n-2)的
结果,最后得到fib(n)。递归调用的过程可以用二叉树的形式表示,如
fib(5)的调用过程如下图所示。
fib(5)
fib(3)
fib(4)
fib(3)
fib(2)
fib(2)
fib(1)
fib(1)
fib(1)
fib(1)
fib(0)
fib(2)
fib(1)
fib(0)
fib(1)
fib(5)递归调用的二叉树表示
递归调用次数即为二叉树的节点个数(深度为n的二叉树最多有2n-1个
节点),即时间复杂度为O(2n)。
4.楼梯上有8级台阶,从下开始往上走,每次可以走一步或者两步,自定义函数fg可以计算走完n级台阶有多少种走法。实现对应功能
的Python程序如下:
def fg(n):
if n==1:
return 1
elif n==2:
return 2
else:
return fg(n-1)+fg(n-2)
Print(‘走完8级台阶的方法共有’,fg(8),‘种’)
则走完这8级台阶的走法有( )
A.34种 B.35种 C.36种 D.37种
A
4.递归过程的实现过程分为两个阶段,分别是( )
A.枚举和回归
B.递推和回归
C.递推和递归
D.试探和回归
B
6.递归算法的函数调用时,处理参数和返回地址通常使用的
数据结构是( )
A.数组
B.队列
C.栈
D.链表
C
谢 谢
5.2.2 递归
大问题的解决中嵌套着与
原问题相似的规模较小的
问题。
这种解决问题的方式在计
算机科学中称为递归,通
过函数自己调用自己来实
现,即一个函数在其定义
中直接或间接调用自身的
一种方法。
在数据结构与算法设计中,递归十分有用,它往往能使函数的定义和算法
的描述简洁且易于理解,极大地减少程序代码量。如前面学过的的二叉树,
由于其本身固有的递归特性,特别适合用递归的形式来描述。
能采用递归描述的算法通常有这样的特征:为求解规模为N的问题,设法将
它分解成规模较小的问题,然后从这些小问题的解中方便地构造出大问题的
解,并且这些规模较小的问题也能采用同样的分解和综合方法。
当递归到达某个边界,如问题规模缩减为0或1时,能直接得解。因此,在设
计递归算法时,要满足两个条件:确定递归公式和递归结束条件。
例:利用递归算法求n的阶乘(n!=1*2*…*n)。由数学知识可知,n阶乘
的递归定义为:它等于n乘以n-1的阶乘,即n!=n*(n-1)!,并且规定0!=1。
设函数fac(n)=n!,则fac(n)可表示为:
fac(n)=
1
(n=0)
n*fac(n-1) (n>0)
按照这个公式,可以将求n!的问题转化成求(n-1)!的问题;而求(n-1)!的问题,
又可以转化成求(n-2)!的问题;求(n-2)!的问题,又可以转化成求(n-3)!的
问题,如此继续,直到最后转化成求0!的问题。再反过来,依次求出1!,
2!,…,直到最后求出n!。因此,在该问题中,递归公式是
fac(n)=n*fac(n-1),当n=0时递归结束。
求n的阶乘的相应的程序及测试结果如下:
def fac(n):
if n==0:
s=1
else:
s=n*fac(n-1)
return s
print(fac(3))
当主程序执行函数fac(3)时,引起第1次函数调用,进入函数后,
参数n=3,应执行计算3*fac(2)。直到计算fac(0),将引起对函数fac的
第4次调用。
以上调用的执行和返回情况,如下图所示。
fac(3)
3*fac(2)
第1次调用
第2次调用
2*fac(1)
第3次调用
1*fac(0)
第4次调用
1
递归调用过程
返回值1
返回值1
返回值2
返回值6
对于阶乘问题,可以在原程序上通过添加一条语句来跟踪参数n的变化
情况:
def fac(n):
if n==0:
s=1
else:
print(str(n)+‘*fac(‘+str(n-1)+’)’)
s=n*fac(n-1)
return s
print(fac(3))
3*fac(2)
2*fac(1)
1*fac(0)
6
利用迭代和递归思想解决问题时有何区别?算法实现时两者有哪些优缺点?
迭代的思想,是一种由旧值不断推出新值的过程。它包括三个方面:
一、确定迭代变量;二、建立迭代关系式;三、控制迭代过程,使
程序能够停止下来。
递归思想,是一种把数据规模较大、较复杂的问题分解成规模较小的问题,
进而构造出整个问题解的思想方法。递归算法的执行过程分递推和回归两
个阶段,其中的关键是如何建立递归关系式与控制程序停止。
一般而言,迭代思想实现的难点在于建立正确的迭代公式,通常要借助
循环语句。而递归思想比较难以理解,程序编写简洁,但递归程序的效率
相对不高。
练习:
1.验证角谷猜想。所谓角谷猜想,是指对于任意一个正整数,若是奇数,
则乘3加1;若是偶数,则除以2。得到的结果再按照上述规则重复处理,
最终总能够得到1。
要求:编写一个程序,输入一个正整数n,把n经过有限次运算后,输出最终变成1的
全过程。
a=int(input(“请输入一个正整数:”))
while a!=1:
print(a)
if a%2==1:
a=a*3+1
else:
a=a//2
print(a)
请输入一个正整数:21
21
64
32
16
8
4
2
1
2.斐波那契数列是这样一个数列:1,1,2,3,5,8,13,21,34,…,其定义如下:
f(0)=0
f(1)=1
f(n)=f(n-1)+f(n-2)(n>=2)
编程求f(40)的值,请分别用迭代和递归算法实现,并分析这两种算法的时间
复杂度。
迭代程序 递归程序
f0=0 f1=1 n=2 while n<=40: f=f1+f0 f0=f1 f1=f n=n+1 print(f1) def fib(n):
if n<1:
return 0
elif n==1:
return 1
else:
return fib(n-1)+fib(n-2)
print(fib(40))
利用迭代算法求斐波那契数列,从n>=2开始计算,用f0和f1两个数相加
求出结果,重复执行n-1次即可,算法的时间复杂度与n成正比,即算法
的时间复杂度为O(n)。
利用递归算法求斐波那契数列,要求解fib(n),必须先计算fib(n-1)和
fib(n-2),计算fib(n-1)和fib(n-2),又必须先计算fib(n-3)和fib(n-4)……
以此类推,直至计算到fib(1)和fib(0),然后回归得到fib(n-1)和fib(n-2)的
结果,最后得到fib(n)。递归调用的过程可以用二叉树的形式表示,如
fib(5)的调用过程如下图所示。
fib(5)
fib(3)
fib(4)
fib(3)
fib(2)
fib(2)
fib(1)
fib(1)
fib(1)
fib(1)
fib(0)
fib(2)
fib(1)
fib(0)
fib(1)
fib(5)递归调用的二叉树表示
递归调用次数即为二叉树的节点个数(深度为n的二叉树最多有2n-1个
节点),即时间复杂度为O(2n)。
4.楼梯上有8级台阶,从下开始往上走,每次可以走一步或者两步,自定义函数fg可以计算走完n级台阶有多少种走法。实现对应功能
的Python程序如下:
def fg(n):
if n==1:
return 1
elif n==2:
return 2
else:
return fg(n-1)+fg(n-2)
Print(‘走完8级台阶的方法共有’,fg(8),‘种’)
则走完这8级台阶的走法有( )
A.34种 B.35种 C.36种 D.37种
A
4.递归过程的实现过程分为两个阶段,分别是( )
A.枚举和回归
B.递推和回归
C.递推和递归
D.试探和回归
B
6.递归算法的函数调用时,处理参数和返回地址通常使用的
数据结构是( )
A.数组
B.队列
C.栈
D.链表
C
谢 谢
