《球的体积和表面积》参考课件
图片预览




文档简介
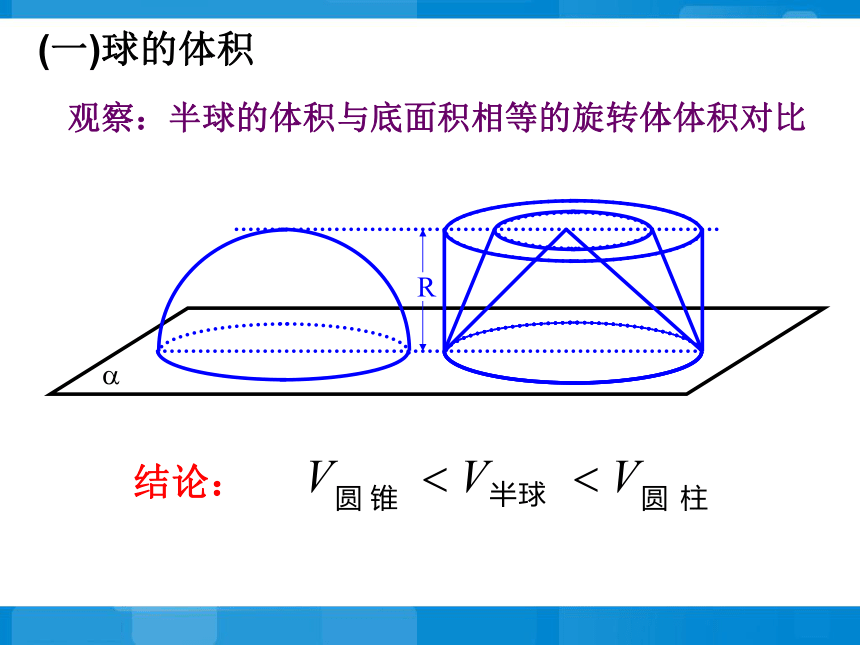
课件18张PPT。1.3.2 球的体积和表面积复习1.柱体的体积公式2.锥体的体积公式3.台体的体积公式V柱体= s hV锥体=V台体=这些公式推导的依据是什么?(一)球的体积 两等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.祖暅原理:思考 : 是否可运用此原理得到球的体积?R?观察:半球的体积与底面积相等的旋转体体积对比结论:(一)球的体积?o设球的半径为R,截面半径为r,平面?与截面的距离为
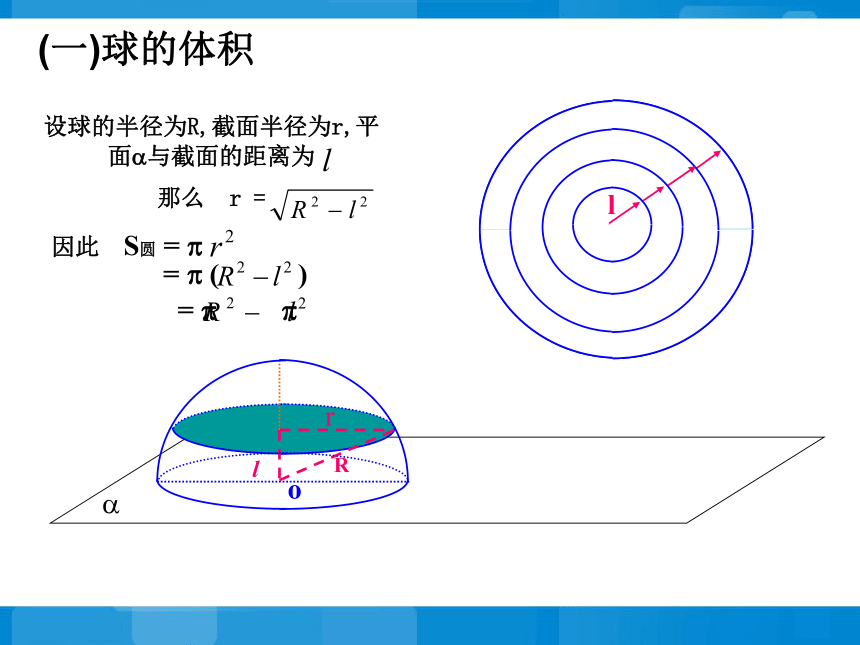
那么 r = (一)球的体积?设球的半径为R,截面半径为r,平面?与截面的距离为
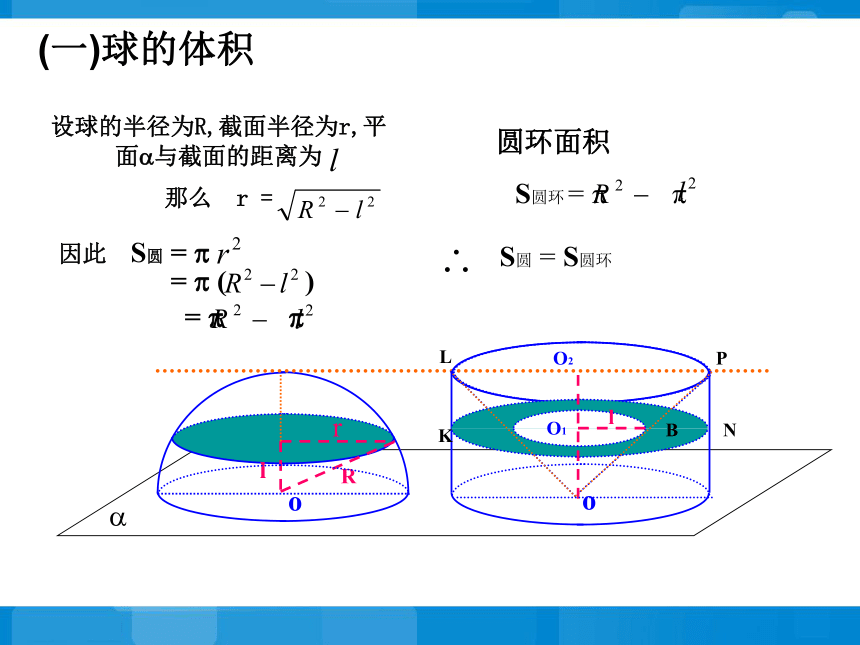
那么 r = (一)球的体积o?S圆 = S圆环 设球的半径为R,截面半径为r,平面?与截面的距离为
那么 r = (一)球的体积?(一)球的体积根据祖暅原理,这两个几何体的体积相等,即
所以 V球 = ? 探究(二)球的表面积分割无限分割逼近精确值R探究(二)球的表面积当n足够大时准锥体例1、(1)钢球直径是5cm,则它的体积为 。
表面积为 。 三、公式的应用(2)某街心花园有许多钢球,每个钢球重145kg,并且外径等于50cm,试根据以上数据,判断钢球是实心的还是空心的.如果是空心的,请你计算出它的内径(钢的密度是7.9g/cm3,π取3.14,结果精确到1cm).解:由于外径为50cm的钢球的质量为: 街心花园中钢球的质量为145000g,而145000<517054,所以钢球是空心的,三、公式的应用解得:答:钢球是空心的.其内径约为45cm.设其内径是2xcm,那么球的质量为:所以2x = 44.8≈45(3)如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)86618515151111x/y/z/三、公式的应用解:这个奖杯的体积为V=V正四棱台+V长方体+ V球 其中V正四棱台V长方=6×8×18=864V球=所以这个奖杯的体积为V ≈ 1828.76(cm3)三、公式的应用例2、(1)把半径为3cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸制作纸盒?球内切于正方体分析:用料最省时,球与正方体有什么位置关系?两个几何体相切:
一个几何体的各个面与另一个几何体的各面相切.三、公式的应用例2、 (2)把正方体的纸盒装入半径为4cm的
球状木盒里,能否装得下? 分析:半径为4cm的球状木盒能装下的最大正
方体与球盒有什么位置关系? 球外接于正方体两个几何体相接:
一个几何体的所有顶点都 在另一个几何体的表面上。三、公式的应用练习:(1)一个正方体内接于半径为R的球内,
则正方体的体积为 。(2)棱长为a的正方体内有一个球与这
个正方体的12条棱都相切,则这个
球的表面积为 。三、公式的应用(3) 有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,则这三个球的体积之比为 .
表面积之比为 .小 结1.球的表面积.
2.体积的计算公式.
那么 r = (一)球的体积?设球的半径为R,截面半径为r,平面?与截面的距离为
那么 r = (一)球的体积o?S圆 = S圆环 设球的半径为R,截面半径为r,平面?与截面的距离为
那么 r = (一)球的体积?(一)球的体积根据祖暅原理,这两个几何体的体积相等,即
所以 V球 = ? 探究(二)球的表面积分割无限分割逼近精确值R探究(二)球的表面积当n足够大时准锥体例1、(1)钢球直径是5cm,则它的体积为 。
表面积为 。 三、公式的应用(2)某街心花园有许多钢球,每个钢球重145kg,并且外径等于50cm,试根据以上数据,判断钢球是实心的还是空心的.如果是空心的,请你计算出它的内径(钢的密度是7.9g/cm3,π取3.14,结果精确到1cm).解:由于外径为50cm的钢球的质量为: 街心花园中钢球的质量为145000g,而145000<517054,所以钢球是空心的,三、公式的应用解得:答:钢球是空心的.其内径约为45cm.设其内径是2xcm,那么球的质量为:所以2x = 44.8≈45(3)如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)86618515151111x/y/z/三、公式的应用解:这个奖杯的体积为V=V正四棱台+V长方体+ V球 其中V正四棱台V长方=6×8×18=864V球=所以这个奖杯的体积为V ≈ 1828.76(cm3)三、公式的应用例2、(1)把半径为3cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸制作纸盒?球内切于正方体分析:用料最省时,球与正方体有什么位置关系?两个几何体相切:
一个几何体的各个面与另一个几何体的各面相切.三、公式的应用例2、 (2)把正方体的纸盒装入半径为4cm的
球状木盒里,能否装得下? 分析:半径为4cm的球状木盒能装下的最大正
方体与球盒有什么位置关系? 球外接于正方体两个几何体相接:
一个几何体的所有顶点都 在另一个几何体的表面上。三、公式的应用练习:(1)一个正方体内接于半径为R的球内,
则正方体的体积为 。(2)棱长为a的正方体内有一个球与这
个正方体的12条棱都相切,则这个
球的表面积为 。三、公式的应用(3) 有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,则这三个球的体积之比为 .
表面积之比为 .小 结1.球的表面积.
2.体积的计算公式.
