江苏省盐城市阜宁县东沟中学2012-2013学年度高一下学期开学考试数学试题
文档属性
| 名称 | 江苏省盐城市阜宁县东沟中学2012-2013学年度高一下学期开学考试数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 243.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-11 00:00:00 | ||
图片预览



文档简介
江苏省盐城市阜宁县东沟中学2012-2013学年度高一下学期开学考试数学试题
一、填空题
1.设是定义在R上的奇函数,且x>0时,,则当时, __________.
2.如图所示,在平面直角坐标系xOy中,角(的终边与单位圆交于点A,点A的纵坐标为,则cos(=_________.
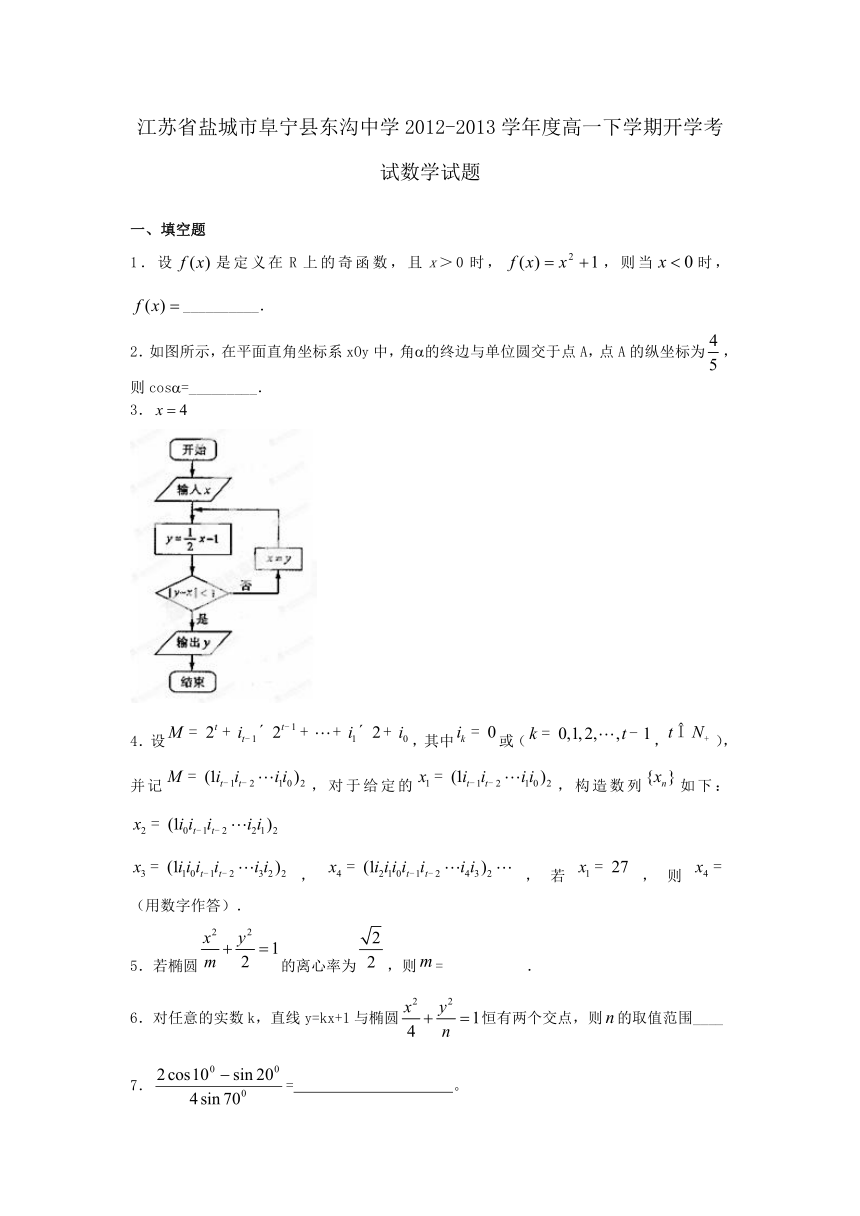
3.
4.设,其中或(,),并记,对于给定的,构造数列如下:
,,若,则 (用数字作答).
5.若椭圆的离心率为,则= .
6.对任意的实数k,直线y=kx+1与椭圆恒有两个交点,则的取值范围____
7.= 。
8.如图,已知PA、PB是圆O的切线,A、B分别为切点,C为圆O上不与A、B重合的另一点,若∠ACB = 120°,则∠APB =
9.已知数列的前项和为,,当时,
.
10.过两点(1,0),(0,2)的直线方程是 .
11.已知函数,数列满足,且数列是单调递增数列,则实数的取值范围是
12.设函数的反函数是,且过点,则经过点 .
13.在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2) < 0的实数x的取值范围为_____________
14.在平面直角坐标系中,对于任意两点与的“非常距离”
给出如下定义:若,则点与点的“非常距离”为,
若,则点与点的“非常距离”为.
已知是直线上的一个动点,点的坐标是(0,1),则点与点的“非常距离”的最小值是_________.
二、解答题
15. 在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)当E 为AB的中点时,求点E到平面ACD1的距离;
(2)AE等于何值时,二面角D1-EC-D的大小为.
16.比较大小(1);(2)。
17.己知,当点在函数的图象上时,点在函数的图象上。
(1)写出的解析式;
(2)求方程的根
18.已知:实数满足,其中;:实数满足,且是的必要不充分条件,求的取值范围。
19.数列{an}的前n项和记为Sn,
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且,又成等比数列,求Tn
20.已知函数.
(1)求f()+f(-)的值;
(2)当x∈ (其中a∈(0, 1), 且a为常数)时,
f(x)是否存在最小值, 若存在, 求出最小值; 若不存在, 请说明理由.
11.
故
一、填空题
1.设是定义在R上的奇函数,且x>0时,,则当时, __________.
2.如图所示,在平面直角坐标系xOy中,角(的终边与单位圆交于点A,点A的纵坐标为,则cos(=_________.
3.
4.设,其中或(,),并记,对于给定的,构造数列如下:
,,若,则 (用数字作答).
5.若椭圆的离心率为,则= .
6.对任意的实数k,直线y=kx+1与椭圆恒有两个交点,则的取值范围____
7.= 。
8.如图,已知PA、PB是圆O的切线,A、B分别为切点,C为圆O上不与A、B重合的另一点,若∠ACB = 120°,则∠APB =
9.已知数列的前项和为,,当时,
.
10.过两点(1,0),(0,2)的直线方程是 .
11.已知函数,数列满足,且数列是单调递增数列,则实数的取值范围是
12.设函数的反函数是,且过点,则经过点 .
13.在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2) < 0的实数x的取值范围为_____________
14.在平面直角坐标系中,对于任意两点与的“非常距离”
给出如下定义:若,则点与点的“非常距离”为,
若,则点与点的“非常距离”为.
已知是直线上的一个动点,点的坐标是(0,1),则点与点的“非常距离”的最小值是_________.
二、解答题
15. 在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)当E 为AB的中点时,求点E到平面ACD1的距离;
(2)AE等于何值时,二面角D1-EC-D的大小为.
16.比较大小(1);(2)。
17.己知,当点在函数的图象上时,点在函数的图象上。
(1)写出的解析式;
(2)求方程的根
18.已知:实数满足,其中;:实数满足,且是的必要不充分条件,求的取值范围。
19.数列{an}的前n项和记为Sn,
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且,又成等比数列,求Tn
20.已知函数.
(1)求f()+f(-)的值;
(2)当x∈ (其中a∈(0, 1), 且a为常数)时,
f(x)是否存在最小值, 若存在, 求出最小值; 若不存在, 请说明理由.
11.
故
同课章节目录
