青岛版七年级数学下册 13.1.4 三角形课件(共27张PPT)
文档属性
| 名称 | 青岛版七年级数学下册 13.1.4 三角形课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-27 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
13.1.4 三角形
1.外角概念及识别
2.自主探索三角形的外角性质和外
角和.
3.掌握三角形的外角性质、外角和
及其应用.
学习目标
重点、难点
重点:三角形外角性质
难点:三角形外角性质及其应用
预设问题
什么是外角?
外角与内角有什么关系?
应用性质时的符号语言?
三角形的外角和是多少?为什么?
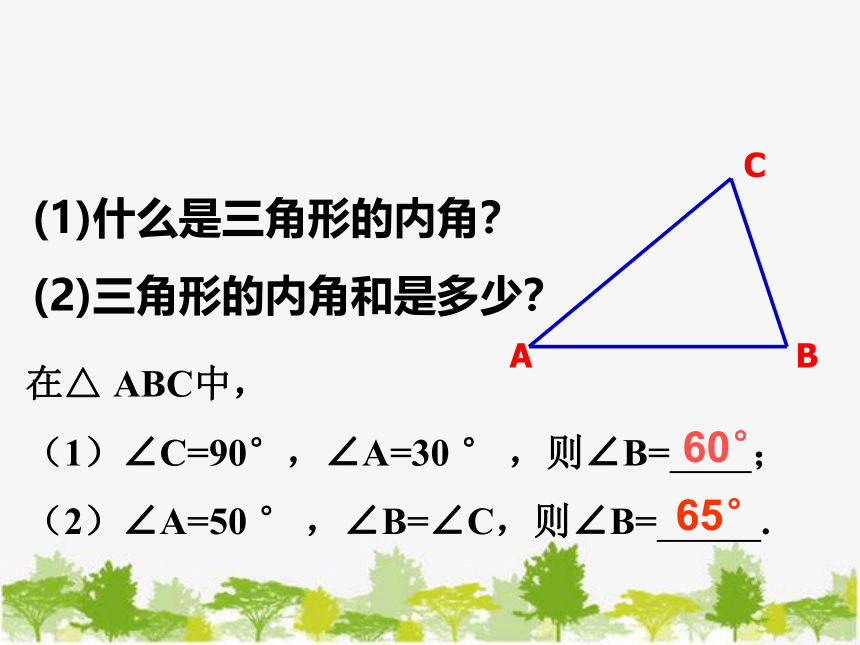
在△ ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
65°
60°
(1)什么是三角形的内角?
(2)三角形的内角和是多少?
B
C
A
A
B
C
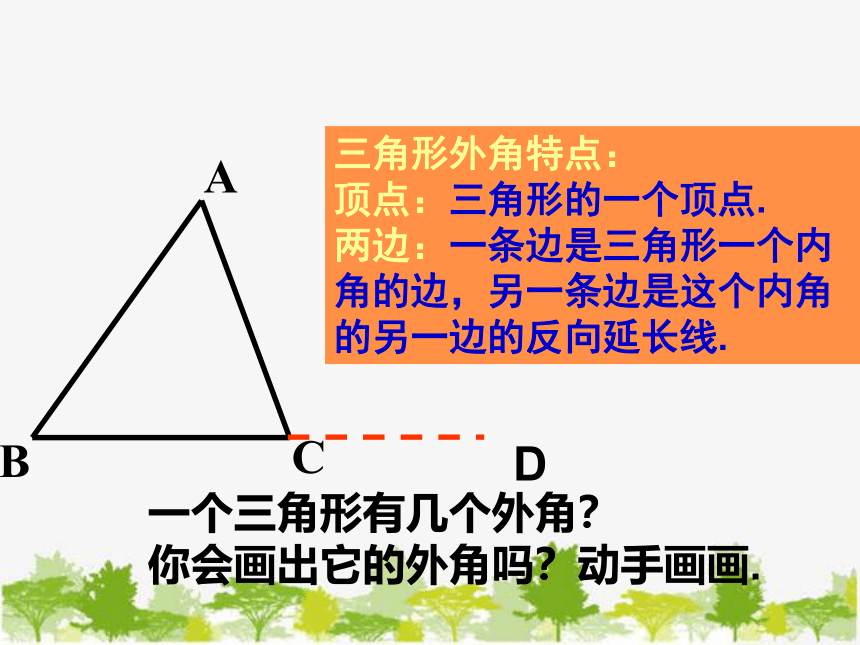
三角形一个角的一边与另一边的反向延长线所组成的角叫三角形的外角.
一个三角形有几个外角?
你会画出它的外角吗?动手画画.
三角形外角特点:
顶点:三角形的一个顶点.
两边:一条边是三角形一个内角的边,另一条边是这个内角的另一边的反向延长线.
D
A
B
C
D
A
B
C
D
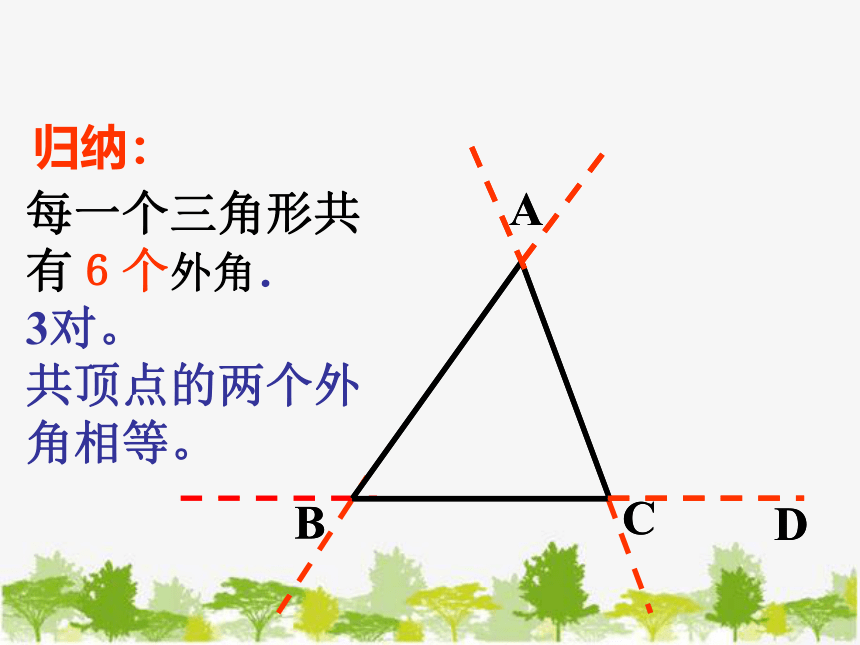
归纳:
每一个三角形共有6个外角.
3对。
共顶点的两个外角相等。
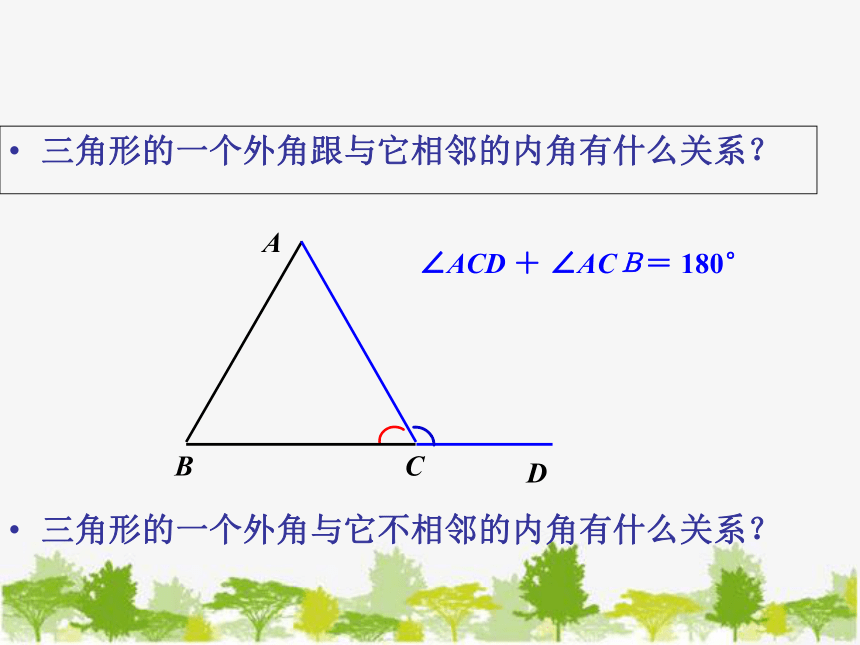
三角形的一个外角跟与它相邻的内角有什么关系?
∠ACD + ∠ACB= 180°
A
B
C
D
三角形的一个外角与它不相邻的内角有什么关系?
三角形的一个外角等于与它不相邻的两个内角的和.
结论:
符号语言:
∵ ∠ACD 是△ABC的外角
∴∠ACD = ∠A + ∠B
证明:
∵∠ACD + ∠ACB=180 ° ∠A+ ∠B+ ∠ACB=180 ° ∴∠ACD= ∠A+ ∠B。
B
C
D
A
A
B
C
D
∵ ∠ACD 是△ABC的外角
∴∠ACD > ∠A ∠ACD > ∠B
三角形的一个外角大于与它不相邻的任何一个内角.
1.观察图形(1),回答问题:
(1)∠AED是 的外角
∠ACD是 的外角.
(2)∠AED = + ,
∠ACD = + .
(3)∠AED > .
∠ACD > .
△CED
△ABC
∠ACD
∠EDC
∠CAB
∠B
∠ACD或∠EDC
∠CAB或∠B
2.求下列各图中∠1 、∠2的度数.
35°
120°
1
∠1=
60°
1
60°
20°
2
∠2=
∠1=
40
85
80
⌒
⌒
60°
55°
A
B
C
D
E
若∠ BAC=
55 , ∠ B=60 ,
则∠ ACD=________,
∠CAE=_________.
1150
1250
1.
4.三角形的一个外角小于与它相邻的 内角,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
C
变式1:三角形的一个外角大于与它相邻的内角,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
D
1.三角形的一个外角与它相邻的
内角____ ;
2.三角形的一个外角____ 与它
不相邻的两个内角的和;
3.三角形的一个外角____ 与它
不相邻的任何一个内角.
等于
大于
互补
例3.如图,已知 ∠ACD=1500, ∠A=2∠B,
求∠ B 的度数.
解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠B,
又∵∠A=2∠B
∴∠ACD=2∠B+∠B=3∠B
又∵∠ACD=1500,
∴3∠B=1500
∴∠B=500
3.如图AB∥CD,∠A=45°,∠C=∠E,
求∠C的度数.
例4.如图,在△ABC中,BD是∠ABC的平分线,∠ABD=∠A,∠C=3∠A
(1)求△ABC的各内角的度数
(2)求∠ADB的度数。
三角形的外角和等于360°
A
B
C
1
2
3
∠1+∠2 +∠3 =
从哪些途径探究这个结果
拓展延伸:
如图(2)P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系:
1、三角形的一个外角小于与它相邻的内角,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
2、如图所示,下列说法错误的是( )
A.∠2=∠A+∠B+∠D B. ∠1=∠2-∠D
C. ∠2=∠A +∠D D. ∠2>∠1 >∠A
2
1
E
D
C
B
A
C
C
3、等腰三角形的一个外角是1000,
则它的顶角的度数为( )
A.800 B.200 C.800或200 D. 500或800
4.如图,直线m∥n, ∠1=55°, ∠2=45°, 求∠3的度数
m
n
3
2
1
C
1、如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,如果∠A=36°,那么∠CDB=_____
2.D为△ABC的边AB上一点,且∠ADC=∠ACD.
求证:∠ACB>∠B .
能力提升
B
C
D
E
A
3.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
⌒
F
G
⌒
2
1
∵∠E+ ∠C= ∠1
解:
∠B+ ∠D= ∠2
∠1 + ∠2 + ∠A = 180°
∴∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
4.如图所示,下列说法错误的是( )
A. ∠2=∠A+∠B+∠D
B. ∠1=∠2-∠D
C. ∠2=∠A +∠D
D. ∠2>∠1 >∠A
C
2
1
E
D
C
B
A
2.三角形外角的两个性质
① 三角形的一个外角等于与它不相邻的两个内角的和。
②三角形的一个外角大于任何一个与它不相邻的内角。
1.三角形外角的定义
三角形外角的性质:
A
C
B
D
2.三角形的一个外角等于与它不相邻的两个内角的和.
3.三角形的一个外角大于与它不相邻的任何一个内角.
符号语言:
1.在△ABC中,
∠ACD= ∠A +∠ B
2.在△ABC中,∠ACD >∠A ,
∠ACD >∠ B
1.三角形的一个外角与它相邻的内角互为邻补角.
13.1.4 三角形
1.外角概念及识别
2.自主探索三角形的外角性质和外
角和.
3.掌握三角形的外角性质、外角和
及其应用.
学习目标
重点、难点
重点:三角形外角性质
难点:三角形外角性质及其应用
预设问题
什么是外角?
外角与内角有什么关系?
应用性质时的符号语言?
三角形的外角和是多少?为什么?
在△ ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
65°
60°
(1)什么是三角形的内角?
(2)三角形的内角和是多少?
B
C
A
A
B
C
三角形一个角的一边与另一边的反向延长线所组成的角叫三角形的外角.
一个三角形有几个外角?
你会画出它的外角吗?动手画画.
三角形外角特点:
顶点:三角形的一个顶点.
两边:一条边是三角形一个内角的边,另一条边是这个内角的另一边的反向延长线.
D
A
B
C
D
A
B
C
D
归纳:
每一个三角形共有6个外角.
3对。
共顶点的两个外角相等。
三角形的一个外角跟与它相邻的内角有什么关系?
∠ACD + ∠ACB= 180°
A
B
C
D
三角形的一个外角与它不相邻的内角有什么关系?
三角形的一个外角等于与它不相邻的两个内角的和.
结论:
符号语言:
∵ ∠ACD 是△ABC的外角
∴∠ACD = ∠A + ∠B
证明:
∵∠ACD + ∠ACB=180 ° ∠A+ ∠B+ ∠ACB=180 ° ∴∠ACD= ∠A+ ∠B。
B
C
D
A
A
B
C
D
∵ ∠ACD 是△ABC的外角
∴∠ACD > ∠A ∠ACD > ∠B
三角形的一个外角大于与它不相邻的任何一个内角.
1.观察图形(1),回答问题:
(1)∠AED是 的外角
∠ACD是 的外角.
(2)∠AED = + ,
∠ACD = + .
(3)∠AED > .
∠ACD > .
△CED
△ABC
∠ACD
∠EDC
∠CAB
∠B
∠ACD或∠EDC
∠CAB或∠B
2.求下列各图中∠1 、∠2的度数.
35°
120°
1
∠1=
60°
1
60°
20°
2
∠2=
∠1=
40
85
80
⌒
⌒
60°
55°
A
B
C
D
E
若∠ BAC=
55 , ∠ B=60 ,
则∠ ACD=________,
∠CAE=_________.
1150
1250
1.
4.三角形的一个外角小于与它相邻的 内角,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
C
变式1:三角形的一个外角大于与它相邻的内角,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
D
1.三角形的一个外角与它相邻的
内角____ ;
2.三角形的一个外角____ 与它
不相邻的两个内角的和;
3.三角形的一个外角____ 与它
不相邻的任何一个内角.
等于
大于
互补
例3.如图,已知 ∠ACD=1500, ∠A=2∠B,
求∠ B 的度数.
解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠B,
又∵∠A=2∠B
∴∠ACD=2∠B+∠B=3∠B
又∵∠ACD=1500,
∴3∠B=1500
∴∠B=500
3.如图AB∥CD,∠A=45°,∠C=∠E,
求∠C的度数.
例4.如图,在△ABC中,BD是∠ABC的平分线,∠ABD=∠A,∠C=3∠A
(1)求△ABC的各内角的度数
(2)求∠ADB的度数。
三角形的外角和等于360°
A
B
C
1
2
3
∠1+∠2 +∠3 =
从哪些途径探究这个结果
拓展延伸:
如图(2)P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系:
1、三角形的一个外角小于与它相邻的内角,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
2、如图所示,下列说法错误的是( )
A.∠2=∠A+∠B+∠D B. ∠1=∠2-∠D
C. ∠2=∠A +∠D D. ∠2>∠1 >∠A
2
1
E
D
C
B
A
C
C
3、等腰三角形的一个外角是1000,
则它的顶角的度数为( )
A.800 B.200 C.800或200 D. 500或800
4.如图,直线m∥n, ∠1=55°, ∠2=45°, 求∠3的度数
m
n
3
2
1
C
1、如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,如果∠A=36°,那么∠CDB=_____
2.D为△ABC的边AB上一点,且∠ADC=∠ACD.
求证:∠ACB>∠B .
能力提升
B
C
D
E
A
3.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
⌒
F
G
⌒
2
1
∵∠E+ ∠C= ∠1
解:
∠B+ ∠D= ∠2
∠1 + ∠2 + ∠A = 180°
∴∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
4.如图所示,下列说法错误的是( )
A. ∠2=∠A+∠B+∠D
B. ∠1=∠2-∠D
C. ∠2=∠A +∠D
D. ∠2>∠1 >∠A
C
2
1
E
D
C
B
A
2.三角形外角的两个性质
① 三角形的一个外角等于与它不相邻的两个内角的和。
②三角形的一个外角大于任何一个与它不相邻的内角。
1.三角形外角的定义
三角形外角的性质:
A
C
B
D
2.三角形的一个外角等于与它不相邻的两个内角的和.
3.三角形的一个外角大于与它不相邻的任何一个内角.
符号语言:
1.在△ABC中,
∠ACD= ∠A +∠ B
2.在△ABC中,∠ACD >∠A ,
∠ACD >∠ B
1.三角形的一个外角与它相邻的内角互为邻补角.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
