7.3万有引力理论的成就(共14张ppt)
文档属性
| 名称 | 7.3万有引力理论的成就(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 548.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-26 16:23:21 | ||
图片预览






文档简介
(共14张PPT)
7.3万有引力理论的成就
学习目标及任务
一、了解万有引力定律在天文学上的重要应用
二、会用万有引力定律计算天体质量
三、掌握运用万有引力定律处理天体问题的思路和方法
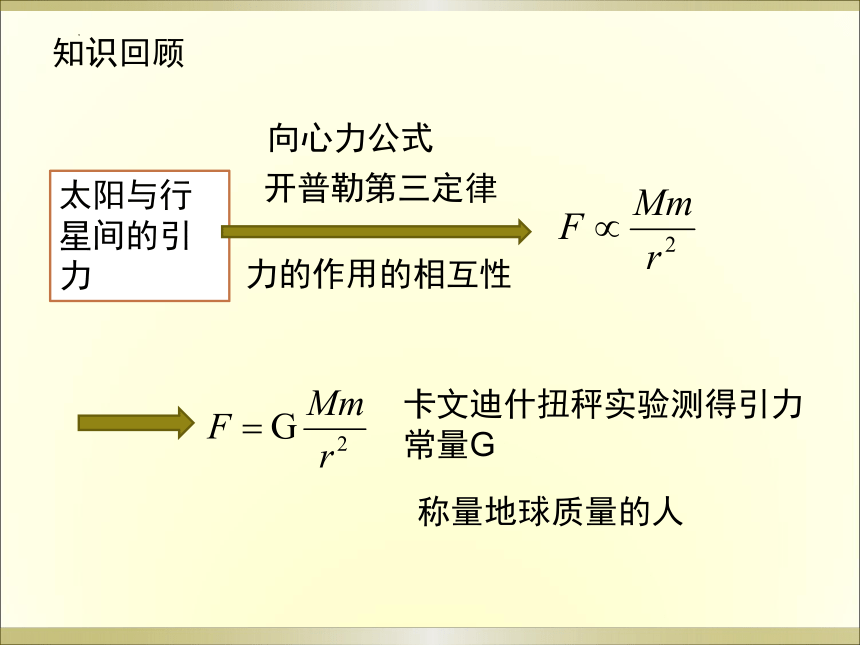
知识回顾
太阳与行星间的引力
向心力公式
开普勒第三定律
力的作用的相互性
卡文迪什扭秤实验测得引力常量G
称量地球质量的人
你能测出我的质量吗
m
m
G=mg
F向
称量地球的质量
若不考虑地球自转的影响,物体所受的重力等于地球对物体的引力。
还有其他方法计算地球质量吗
称量地球的质量
月球绕地球公转的周期为T,轨道半径为r
1、计算中心天体的质量
思路一(环绕法):将行星绕恒星的运动、卫星绕行星的运动视为匀速圆周运动,所需向心力是由万有引力提供的。
思路二(重力加速度法):中心天体表面上物体的重力与所受万有引力相等。
如何计算太阳的质量
求解思路:环绕天体的向心力由中心天体对其万有引力提供
太阳作为中心天体M
环绕天体m
具体方法:
你能求出太阳的平均密度吗?
如何求中心天体的平均密度呢?
r为卫星运行轨道的半径
R为中心天体的半径
当天体的卫星环绕天体表面做匀速圆周运动时,其轨道半径r约等于天体的半径R,则天体的平均密度为
2、发现未知天体
海王星的发现:在18世纪,人们已经知道太阳系有7个行星,其中1781年发现的第七个行星--天王星的运动轨道,总是同根据万有引力定律计算出来的有比较大的偏离,当时有人推测,在天王星轨道外面还有一个未发现的行星,它对天王星的作用引起了上述偏离。英国剑桥大学的学生亚当斯和法国年轻的天文学家勒维耶根据天王星的观测资料,各自独立地利用万有引力定律计算出这颗新行星的轨道。1846年9月23日晚,德国的加勒在勒维耶预言的位置附近发现了这颗新行星。后来,天文学家把这个行星叫做海王星。
预言哈雷彗星回归:英国天文学家哈雷依据万有引力定律,用一年时间计算24颗彗星的轨道,并大胆猜测在1531年、1607年、1682年出现的三颗彗星是同一颗星,周期约为76年。
海王星的发现和哈雷彗星的“按时回归”确立了万有引力定律的地位。
例1:(1)开普勒第三定律指出:行星绕太阳运动椭圆轨道的半长轴a的三次方与它的公转周期T的二次方之比是定值,即 , k是一个对所有行星都相同的常量。将行星绕太阳的运动简化成圆周运动处理,请你推导出太阳系中该常量k的表达式(已知引力常量为G,太阳的质量为M);
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84x108m,月球绕地球运动的周期为2.36x106s,地球半径取6400km,试估算地球的质量M和平均密度 。(G=6.67x10-11N.m2/kg2,计算结果均保留一位有效数字)
(1)根据牛顿第三定律:
(2)在地月系统中
例2:某星球的半径为R,表面的重力加速度为g,引力常量为G,则该星球的平均密度为( )
B
在星球附近
小结
1.了解了万有引力定律在天文学中具有的重要意义
2.掌握了应用万有引力定律解决天文学中问题的两条思路
7.3万有引力理论的成就
学习目标及任务
一、了解万有引力定律在天文学上的重要应用
二、会用万有引力定律计算天体质量
三、掌握运用万有引力定律处理天体问题的思路和方法
知识回顾
太阳与行星间的引力
向心力公式
开普勒第三定律
力的作用的相互性
卡文迪什扭秤实验测得引力常量G
称量地球质量的人
你能测出我的质量吗
m
m
G=mg
F向
称量地球的质量
若不考虑地球自转的影响,物体所受的重力等于地球对物体的引力。
还有其他方法计算地球质量吗
称量地球的质量
月球绕地球公转的周期为T,轨道半径为r
1、计算中心天体的质量
思路一(环绕法):将行星绕恒星的运动、卫星绕行星的运动视为匀速圆周运动,所需向心力是由万有引力提供的。
思路二(重力加速度法):中心天体表面上物体的重力与所受万有引力相等。
如何计算太阳的质量
求解思路:环绕天体的向心力由中心天体对其万有引力提供
太阳作为中心天体M
环绕天体m
具体方法:
你能求出太阳的平均密度吗?
如何求中心天体的平均密度呢?
r为卫星运行轨道的半径
R为中心天体的半径
当天体的卫星环绕天体表面做匀速圆周运动时,其轨道半径r约等于天体的半径R,则天体的平均密度为
2、发现未知天体
海王星的发现:在18世纪,人们已经知道太阳系有7个行星,其中1781年发现的第七个行星--天王星的运动轨道,总是同根据万有引力定律计算出来的有比较大的偏离,当时有人推测,在天王星轨道外面还有一个未发现的行星,它对天王星的作用引起了上述偏离。英国剑桥大学的学生亚当斯和法国年轻的天文学家勒维耶根据天王星的观测资料,各自独立地利用万有引力定律计算出这颗新行星的轨道。1846年9月23日晚,德国的加勒在勒维耶预言的位置附近发现了这颗新行星。后来,天文学家把这个行星叫做海王星。
预言哈雷彗星回归:英国天文学家哈雷依据万有引力定律,用一年时间计算24颗彗星的轨道,并大胆猜测在1531年、1607年、1682年出现的三颗彗星是同一颗星,周期约为76年。
海王星的发现和哈雷彗星的“按时回归”确立了万有引力定律的地位。
例1:(1)开普勒第三定律指出:行星绕太阳运动椭圆轨道的半长轴a的三次方与它的公转周期T的二次方之比是定值,即 , k是一个对所有行星都相同的常量。将行星绕太阳的运动简化成圆周运动处理,请你推导出太阳系中该常量k的表达式(已知引力常量为G,太阳的质量为M);
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84x108m,月球绕地球运动的周期为2.36x106s,地球半径取6400km,试估算地球的质量M和平均密度 。(G=6.67x10-11N.m2/kg2,计算结果均保留一位有效数字)
(1)根据牛顿第三定律:
(2)在地月系统中
例2:某星球的半径为R,表面的重力加速度为g,引力常量为G,则该星球的平均密度为( )
B
在星球附近
小结
1.了解了万有引力定律在天文学中具有的重要意义
2.掌握了应用万有引力定律解决天文学中问题的两条思路
