华东师大新版2022年七年级下册 第6章 一元一次方程 单元测试卷3(word版含解析)
文档属性
| 名称 | 华东师大新版2022年七年级下册 第6章 一元一次方程 单元测试卷3(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 234.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-27 00:00:00 | ||
图片预览




文档简介
华东师大新版七年级下册《第6章一元一次方程》 2022年单元测试卷(3)
副标题
题号 一 二 三 四 总分
得分
一、选择题(本大题共8小题,共24.0分)
下列是二元一次方程的是
A. B.
C. D.
下列各方程组中,不是二元一次方程组的是
A. B.
C. D.
甲、乙两人同求方程的整数解,甲正确地求出一个解为,乙把看成,求得一个解为,则,的值分别为
A. B. C. D.
九年级的数学老师平均每月上节辅导课,如果由女教师完成,则每人每月应上节;如果只由男教师完成,则每人应上辅导课节.
A. B. C. D.
我国古代数学名著孙子算经中记载了一道题,大意是:有匹马恰好拉了片瓦,已知匹大马能拉片瓦,匹小马能拉片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为
A. B.
C. D.
瑞安市万松宾馆有单人间、双人间、三人间三种客房供游客选择居住,现某旅游团有名旅客同时安排居住在这三种客房,若每个房间都住满,共需间,则居住方案有
A. 种 B. 种 C. 种 D. 种
解方程组:;;;比较适宜的方法是
A. 用代入法,用加减法 B. 用代入法,用加减法
C. 用代入法,用加减法 D. 用代入法,用加减法
若与互为相反数,则的值为
A. B. C. D.
二、填空题(本大题共8小题,共24.0分)
若与是同类项,则 ______ , ______ .
已知甲队有人,乙队有人,若从甲队调出人到乙队,则乙队人数是甲队人数的倍,调整后两队人数间的数量关系用等式表示为______;
现有参观爱国丰义教育基地的参观券若干张,分给若干名同学,若每人张则多张,若每人张则少张.问有多少张参观券,多少名同学?若设有张参观券,有名同学,根据题意,可列出关于、的二元一次方程组为______ .
一个两位数的十位数字与个位数字之和等于,十位数字与个位数字之差为,设十位数字为,个位数字为,则用方程组表示上述语言为______ .
某人骑自行车由甲地驶向乙地,如果每小时比原来的速度快公里,便可以早到分钟;如果每小时比原来的速度慢公里,便要迟到分钟.则甲、乙两地的距离为______公里.
已知是方程组的解,则 ______ .
打折前,买件商品和件商品用了元,买件商品和件商品用了元,打折后,买件商品和件商品用了元,比不打折时,一共少花了______元.
五羊公园门票规定为:每人元;人以上的团体购票,每人元,每人优惠人免票不足人的余数不优惠今有花城旅行社、穗城旅行社、羊城旅行社的三支旅游团前来参观:如果花城团、穗城团合起来作为一个团体购票,应购门票元;如果穗城团、羊城团合起来购票,应购门票元;如果羊城团、花城团合起来购票,应购门票元,那么三个团共有人______.
三、计算题(本大题共3小题,共27.0分)
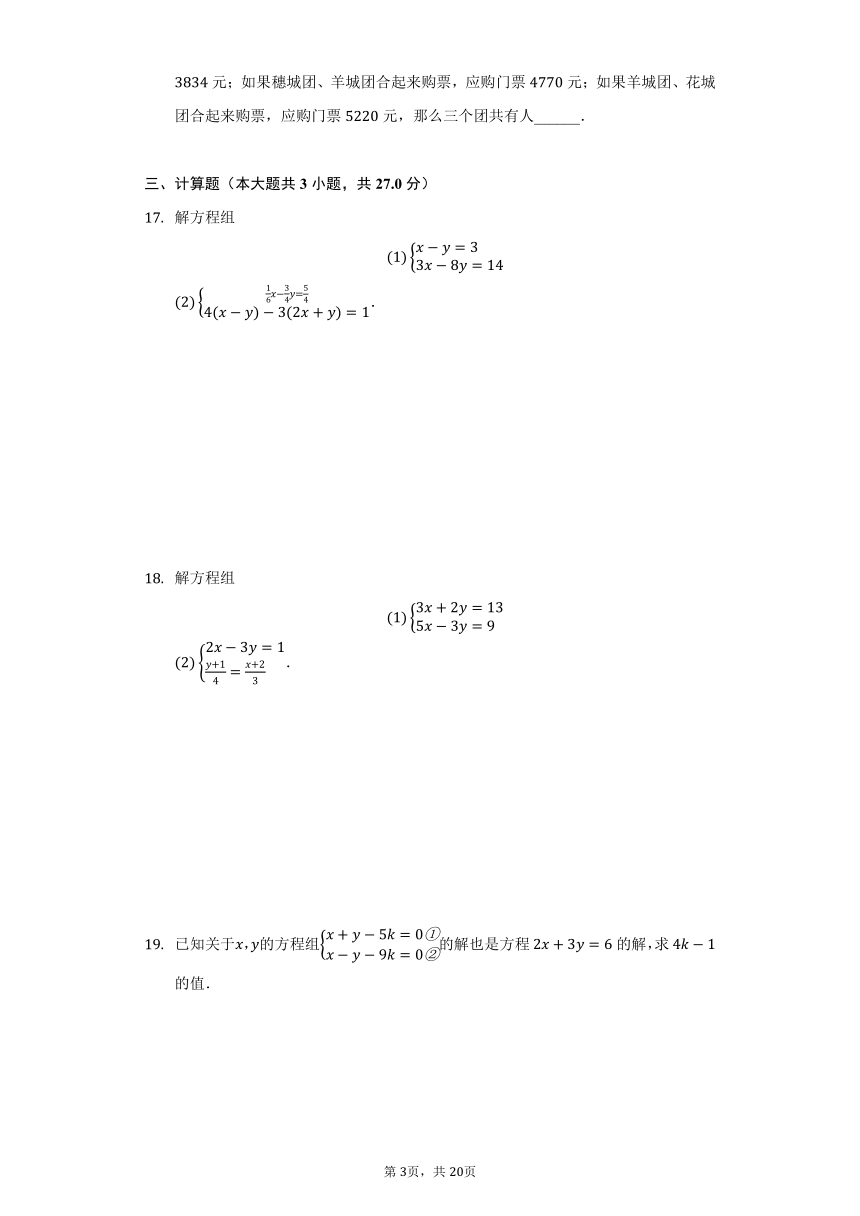
解方程组
.
解方程组
.
已知关于,的方程组的解也是方程的解,求的值.
四、解答题(本大题共5小题,共45.0分)
如果方程组的解满足,求的值.
在某工程建设中,有甲、乙两种卡车参加运土,辆甲种卡车与辆乙种卡车一次共可运土立方米,辆甲种卡车与辆乙种卡车一次共可运土立方米,辆甲种卡车与辆乙种卡车一次共可运土多少立方米?
某专卖店有,两种商品.已知在打折前,买件商品和件商品用了元;买件商品和件商品用了元.,两种商品打相同折以后,某人买件商品和件商品一共比不打折少花元,计算打了多少折?
利用方程或方程组解决下面问题:
某精工商城计划拨款万元从厂家购进台加工机械,已知该厂生产三种不同型号的加工机械,出厂价分别为:甲种每台万元,乙种每台万元,丙种每台万元.
若商城同时购进其中两种不同型号加工机械共台,用去万元,请你研究一下商城的进货方案;
若商城销售一台甲种加工机械可获利元,销售一台乙种加工机械可获利元,销售一台丙种加工机械可获利元,在同时购进两种不同型号加工机械的方案中,为使销售利润最多,你选择哪一种进货方案?
阅读材料,善于思考的小军在解方程组时,采用了一种“整体代换”的解法:
解:将方程变形:
即
把方程代入得:
把代入得
方程组的解为
请你解决以下问题:
模仿小军的“整体代换”法解方程组
已知、满足方程组
求的值;
求的值.
答案和解析
1.【答案】
【解析】
解:、是二元二次方程,故选项错误;
B、是分式方程,故选项错误;
C、是二元一次方程,故选项正确;
D、是三元一次方程,故选项错误.
故选:.
二元一次方程满足的条件:含有个未知数,未知数的项的次数是的整式方程.
主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有个未知数,未知数的项的次数是的整式方程.
2.【答案】
【解析】
解:、、均满足二元一次方程组的定义;
中的是二次项.
故选:.
二元一次方程的定义:含有两个未知数,并且未知数的项的最高次数是的方程叫二元一次方程.
二元一次方程组的定义:由两个二元一次方程组成的方程组叫二元一次方程组.
此题考查了二元一次方程的定义和二元一次方程组的定义.
注意:是最简单的二元一次方程组.
3.【答案】
【解析】
解:把代入中得:
,
把代入中得:
,
把组成方程组得:,
解得:,
故选:.
首先根据题意把代入中得,把代入中得:,组成方程组可解得,的值.
此题主要考查了二元一次方程组的解,关键是正确把握二元一次方程的解的定义.
4.【答案】
【解析】
解:设九年级有男老师名,女老师名,只由男老师上辅导课的节数为节,
由题意可得:,
解得节.
故选:.
根据九年级数学老师上的辅导课的总量不变,分别根据男女老师完成上课可以得到两个等量关系,即可求出由男老师上辅导课的节数.
解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出个等量关系,准确地找到等量关系并用方程组表示出来是解题的关键.
5.【答案】
【解析】
解:设大马有匹,小马有匹,由题意得:
,
故选:.
设大马有匹,小马有匹,根据题意可得等量关系:大马数小马数;大马拉瓦数小马拉瓦数,根据等量关系列出方程组即可.
此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程组.
6.【答案】
【解析】
解:设租一人间间,租二人间间,则三人间客房间.
依题意得:,
解得:,
,
,,是正整数,
当时,,不符合题意,舍去;
当时,,不符合题意,舍去;
当时,,;
当时,,;
当时,,;
当时,,;不符合题意,舍去;
居住方案有种.
故选:.
找出关键描述语为:某旅行团人准备同时选择这三种客房共间,每个房间都住满,可先列出函数关系式,再根据已知条件确定所求未知量的范围,从而确定居住方案.
此题考查了三元一次不定方程组的应用.此题难度较大,解题的关键是理解题意,根据题意列方程组,然后根据,,是整数求解,注意分类讨论思想的应用.
7.【答案】
【解析】
解:解方程组:;;;比较适宜的方法是:用代入法,用加减法.
故选:.
方程,每个方程组中的一个未知数很容易用含另一个未知数的代数式表示出来,所以比较适宜的方法是代入法;
方程,每个方程组中的同一个未知数的系数既不相等又不互为相反数,就用适当的数去乘方程的两边,使某一个未知数的系数相等或互为相反数,所以比较适宜的方法是加减法.
此题主要考查了解二元一次方程组的方法,注意代入消元法和加减消元法的应用.
8.【答案】
【解析】
解:与互为相反数,
,
,,
.
故选:.
先根据相反数的定义列出关于、的方程,求出、的值即可.
本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.
9.【答案】
;
【解析】
解:与是同类项,
,
解得.
故答案为:,.
先根据同类项的定义得出关于、的方程组,求出的值即可.
本题考查的是同类项,即所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
10.【答案】
【解析】
解:设甲队有人,乙队有人,
由题意,知
.
故答案为:
本题的等量关系有:甲队调出人到乙队,则乙队人数是甲队人数的倍,可以列出方程.
此题考查二元一次方程的应用,根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.
11.【答案】
【解析】
解:设有张参观券,有名同学,
由题意得,.
故答案为.
设有张参观券,有名同学,根据每人张则多张,每人张则少张,列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是根据题意,找出等量关系.
12.【答案】
【解析】
解:由题意,有.
题中有两个等量关系:十位数字个位数字;十位数字个位数字.
根据这两个等量关系即可列出方程组.
读懂题意,找出等量关系是列方程解应用题的关键.
本题比较简单.注意十位数字与个位数字之差即为十位数字个位数字,而不是个位数字十位数字.
13.【答案】
【解析】
解:设此人正常的速度为,行走的时间为,
则由题意知:,
,
化简得;
,
解得,,
甲乙两地的距离为公里.
答:甲乙两地的距离为公里.
设此人正常的速度为,行走的时间为,则根据如果每小时比原来的速度快公里,便可以早到分钟;如果每小时比原来的速度慢公里,便要迟到分钟列出关于、的方程组,求得、的值即可求解.
本题考查了二元一次方程组的应用,本题中列出关于、的方程组并且求、的值是解题的关键.
14.【答案】
【解析】
解:根据题意得,,
解得,
所以.
故答案为:.
根据方程组解的定义,把解代入方程组得到关于、的方程,然后求解得到、的值,再代入代数式进行计算即可得解.
本题考查了二元一次方程组的解,根据解的定义得到关于、的方程组并求出、的值是解题的关键.
15.【答案】
【解析】
解:设打折前商品每件元,商品每件元,根据题意,得:
,
解得:,
打折前买件商品和件商品需要元,
则打折后比打折前少花元,
故答案为:.
设打折前商品每件元,商品每件元,根据买件商品和件商品用了元;买件商品和件商品用了元.可列出方程组求得、商品的单件,继而可得打折前买件商品和件商品所需总费用,比较即可得答案.
考查了二元一次方程组的应用,解题关键是弄清题意,合适的等量关系,列出方程组,熟练运用代入消元法或加减消元法解方程组.
16.【答案】
【解析】
解:设花城团有人,穗城团有人,羊城团有人,
因为,,,
又,,.
根据公园门票优惠方法得方程组:,即;
,即;
,即.
三式相加得:,故,即三个团共有人.
由可知,穗城团与羊城团合起来有人,而应写成,即人只需有人买票,与题目中的不符.因此,穗城团、羊城团的人数加起来不可能是人而应是人,而,因为只有人才需要购买人的票,同样,由人,若再增加一人,变为人,则,省人的票,同样也是人买票.所以羊城团、花城团合起来可能是人,也可能是人.即可能是,也可能是综上所述,可得方程组: 或
由方程组可得:,故,
由方程组可得:,故,由于人数不可能为小数,
所以方程组不符合实际,应舍去,故三个团共有人.
故答案为:.
可设花城团有人,穗城团有人,羊城团有人,每人元,每人优惠人免票不足人的余数不优惠,实际上就是:元,可进人.可得方程组: 或,解方程组求解即可.
本题考查了三元一次方程组的应用,解题的关键是得出羊城团、花城团合起来可能是人,也可能是人,从而根据情况舍去不符合实际的.
17.【答案】
解:,
得:,即,
把代入得:,
则方程组的解为;
方程组整理得:,
得:,即,
把代入得:,
则方程组的解为.
【解析】
方程组利用加减消元法求出解即可;
方程组整理后,利用加减消元法求出解即可.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
18.【答案】
解:,
得:,
解得:,
把代入得:,
则方程组的解为;
方程组整理得:,
得:,
解得:,
把代入得:,
则方程组的解为.
【解析】
方程组利用加减消元法求出解即可;
方程组整理后,利用加减消元法求出解即可.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
19.【答案】
解:得:,
得:,
代入中,得:,
解得:.
则
【解析】
把看作已知数表示出方程组的解得到与,代入已知方程计算求出的值,即可求出原式的值.
此题考查了二元一次方程组的解,以及二元一次方程的解,熟练掌握运算法则是解本题的关键.
20.【答案】
解:解原方程组得,,
,
,解得,
.
【解析】
先用表示出方程组的解,再代入即可求出的值,代入代数式即可得出结论.
本题考查的是二元一次方程组的解,根据题意得出关于的一元一次方程是解答此题的关键.
21.【答案】
解:设辆甲种卡车一次可运土立方米,辆乙种卡车一次可运土立方米,
依题意,得:,
解得:,
.
答:辆甲种卡车与辆乙种卡车一次共可运土立方米.
【解析】
设辆甲种卡车一次可运土立方米,辆乙种卡车一次可运土立方米,根据“辆甲种卡车与辆乙种卡车一次共可运土立方米,辆甲种卡车与辆乙种卡车一次共可运土立方米”,即可得出关于,的二元一次方程组,解之即可得出,的值,再将其代入中即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
22.【答案】
解:设打折前商品的单价为元件,商品的单价为元件,
根据题意得:
解得:.
打折前,购买件商品和件商品一共要用元,
打折后,购买件商品和件商品一共要用元,
.
答:打了八折.
【解析】
设打折前商品的单价为元件,商品的单价为元件,根据“买件商品和件商品用了元;买件商品和件商品用了元”,即可得出关于、的二元一次方程组,解之即可得出、值,利用总价单价数量求出打折前所需费用,结合打折后少花的钱数即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
23.【答案】
解:设购买加工机械甲种台,乙种台,丙种台,由题意得:
,
解得:;
,
解得:舍去
,
解得:.
故两种方案:方案:甲种加工机械台,乙种加工机械台;
方案:购买甲种加工机械台,乙种加工机械台;
选择方案,理由:
商场销售一台甲种加工机械可获利元,销售一台乙种加工机械机可获利元,销售一台丙种加工机械可获利元,
方案:元,
方案:元,
故选择方案.
【解析】
通过理解题意可知本题存在两个等量关系,即“购进其中两种不同型号的加工机械共台”和“两种不同型号的加工机械共用去万元”,根据这两个等量关系可列出方程组.
根据中两种方案,分别求出利润即可.
此题主要考查了二元一次方程组的应用以及最佳方案问题,根据已知得出总钱数和总台数的方程是解题关键.
24.【答案】
解:由得:,即,
把代入得:,即,
把代入得:,
则方程组的解为;
由得:,即,
由得:,即,
整理得:,
;
,,
,即,
则原式.
【解析】
方程组中第二个方程变形后,将第一个方程代入求出的值,进而求出的值,得到方程组的解;
方程组第一个方程变形表示出,第二个方程变形后代入求出的值,进而求出的值;
利用完全平方公式及平方根定义求出的值,再由的值,即可求出所求式子的值.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
第2页,共2页
第1页,共1页
副标题
题号 一 二 三 四 总分
得分
一、选择题(本大题共8小题,共24.0分)
下列是二元一次方程的是
A. B.
C. D.
下列各方程组中,不是二元一次方程组的是
A. B.
C. D.
甲、乙两人同求方程的整数解,甲正确地求出一个解为,乙把看成,求得一个解为,则,的值分别为
A. B. C. D.
九年级的数学老师平均每月上节辅导课,如果由女教师完成,则每人每月应上节;如果只由男教师完成,则每人应上辅导课节.
A. B. C. D.
我国古代数学名著孙子算经中记载了一道题,大意是:有匹马恰好拉了片瓦,已知匹大马能拉片瓦,匹小马能拉片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为
A. B.
C. D.
瑞安市万松宾馆有单人间、双人间、三人间三种客房供游客选择居住,现某旅游团有名旅客同时安排居住在这三种客房,若每个房间都住满,共需间,则居住方案有
A. 种 B. 种 C. 种 D. 种
解方程组:;;;比较适宜的方法是
A. 用代入法,用加减法 B. 用代入法,用加减法
C. 用代入法,用加减法 D. 用代入法,用加减法
若与互为相反数,则的值为
A. B. C. D.
二、填空题(本大题共8小题,共24.0分)
若与是同类项,则 ______ , ______ .
已知甲队有人,乙队有人,若从甲队调出人到乙队,则乙队人数是甲队人数的倍,调整后两队人数间的数量关系用等式表示为______;
现有参观爱国丰义教育基地的参观券若干张,分给若干名同学,若每人张则多张,若每人张则少张.问有多少张参观券,多少名同学?若设有张参观券,有名同学,根据题意,可列出关于、的二元一次方程组为______ .
一个两位数的十位数字与个位数字之和等于,十位数字与个位数字之差为,设十位数字为,个位数字为,则用方程组表示上述语言为______ .
某人骑自行车由甲地驶向乙地,如果每小时比原来的速度快公里,便可以早到分钟;如果每小时比原来的速度慢公里,便要迟到分钟.则甲、乙两地的距离为______公里.
已知是方程组的解,则 ______ .
打折前,买件商品和件商品用了元,买件商品和件商品用了元,打折后,买件商品和件商品用了元,比不打折时,一共少花了______元.
五羊公园门票规定为:每人元;人以上的团体购票,每人元,每人优惠人免票不足人的余数不优惠今有花城旅行社、穗城旅行社、羊城旅行社的三支旅游团前来参观:如果花城团、穗城团合起来作为一个团体购票,应购门票元;如果穗城团、羊城团合起来购票,应购门票元;如果羊城团、花城团合起来购票,应购门票元,那么三个团共有人______.
三、计算题(本大题共3小题,共27.0分)
解方程组
.
解方程组
.
已知关于,的方程组的解也是方程的解,求的值.
四、解答题(本大题共5小题,共45.0分)
如果方程组的解满足,求的值.
在某工程建设中,有甲、乙两种卡车参加运土,辆甲种卡车与辆乙种卡车一次共可运土立方米,辆甲种卡车与辆乙种卡车一次共可运土立方米,辆甲种卡车与辆乙种卡车一次共可运土多少立方米?
某专卖店有,两种商品.已知在打折前,买件商品和件商品用了元;买件商品和件商品用了元.,两种商品打相同折以后,某人买件商品和件商品一共比不打折少花元,计算打了多少折?
利用方程或方程组解决下面问题:
某精工商城计划拨款万元从厂家购进台加工机械,已知该厂生产三种不同型号的加工机械,出厂价分别为:甲种每台万元,乙种每台万元,丙种每台万元.
若商城同时购进其中两种不同型号加工机械共台,用去万元,请你研究一下商城的进货方案;
若商城销售一台甲种加工机械可获利元,销售一台乙种加工机械可获利元,销售一台丙种加工机械可获利元,在同时购进两种不同型号加工机械的方案中,为使销售利润最多,你选择哪一种进货方案?
阅读材料,善于思考的小军在解方程组时,采用了一种“整体代换”的解法:
解:将方程变形:
即
把方程代入得:
把代入得
方程组的解为
请你解决以下问题:
模仿小军的“整体代换”法解方程组
已知、满足方程组
求的值;
求的值.
答案和解析
1.【答案】
【解析】
解:、是二元二次方程,故选项错误;
B、是分式方程,故选项错误;
C、是二元一次方程,故选项正确;
D、是三元一次方程,故选项错误.
故选:.
二元一次方程满足的条件:含有个未知数,未知数的项的次数是的整式方程.
主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有个未知数,未知数的项的次数是的整式方程.
2.【答案】
【解析】
解:、、均满足二元一次方程组的定义;
中的是二次项.
故选:.
二元一次方程的定义:含有两个未知数,并且未知数的项的最高次数是的方程叫二元一次方程.
二元一次方程组的定义:由两个二元一次方程组成的方程组叫二元一次方程组.
此题考查了二元一次方程的定义和二元一次方程组的定义.
注意:是最简单的二元一次方程组.
3.【答案】
【解析】
解:把代入中得:
,
把代入中得:
,
把组成方程组得:,
解得:,
故选:.
首先根据题意把代入中得,把代入中得:,组成方程组可解得,的值.
此题主要考查了二元一次方程组的解,关键是正确把握二元一次方程的解的定义.
4.【答案】
【解析】
解:设九年级有男老师名,女老师名,只由男老师上辅导课的节数为节,
由题意可得:,
解得节.
故选:.
根据九年级数学老师上的辅导课的总量不变,分别根据男女老师完成上课可以得到两个等量关系,即可求出由男老师上辅导课的节数.
解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出个等量关系,准确地找到等量关系并用方程组表示出来是解题的关键.
5.【答案】
【解析】
解:设大马有匹,小马有匹,由题意得:
,
故选:.
设大马有匹,小马有匹,根据题意可得等量关系:大马数小马数;大马拉瓦数小马拉瓦数,根据等量关系列出方程组即可.
此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程组.
6.【答案】
【解析】
解:设租一人间间,租二人间间,则三人间客房间.
依题意得:,
解得:,
,
,,是正整数,
当时,,不符合题意,舍去;
当时,,不符合题意,舍去;
当时,,;
当时,,;
当时,,;
当时,,;不符合题意,舍去;
居住方案有种.
故选:.
找出关键描述语为:某旅行团人准备同时选择这三种客房共间,每个房间都住满,可先列出函数关系式,再根据已知条件确定所求未知量的范围,从而确定居住方案.
此题考查了三元一次不定方程组的应用.此题难度较大,解题的关键是理解题意,根据题意列方程组,然后根据,,是整数求解,注意分类讨论思想的应用.
7.【答案】
【解析】
解:解方程组:;;;比较适宜的方法是:用代入法,用加减法.
故选:.
方程,每个方程组中的一个未知数很容易用含另一个未知数的代数式表示出来,所以比较适宜的方法是代入法;
方程,每个方程组中的同一个未知数的系数既不相等又不互为相反数,就用适当的数去乘方程的两边,使某一个未知数的系数相等或互为相反数,所以比较适宜的方法是加减法.
此题主要考查了解二元一次方程组的方法,注意代入消元法和加减消元法的应用.
8.【答案】
【解析】
解:与互为相反数,
,
,,
.
故选:.
先根据相反数的定义列出关于、的方程,求出、的值即可.
本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.
9.【答案】
;
【解析】
解:与是同类项,
,
解得.
故答案为:,.
先根据同类项的定义得出关于、的方程组,求出的值即可.
本题考查的是同类项,即所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
10.【答案】
【解析】
解:设甲队有人,乙队有人,
由题意,知
.
故答案为:
本题的等量关系有:甲队调出人到乙队,则乙队人数是甲队人数的倍,可以列出方程.
此题考查二元一次方程的应用,根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.
11.【答案】
【解析】
解:设有张参观券,有名同学,
由题意得,.
故答案为.
设有张参观券,有名同学,根据每人张则多张,每人张则少张,列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是根据题意,找出等量关系.
12.【答案】
【解析】
解:由题意,有.
题中有两个等量关系:十位数字个位数字;十位数字个位数字.
根据这两个等量关系即可列出方程组.
读懂题意,找出等量关系是列方程解应用题的关键.
本题比较简单.注意十位数字与个位数字之差即为十位数字个位数字,而不是个位数字十位数字.
13.【答案】
【解析】
解:设此人正常的速度为,行走的时间为,
则由题意知:,
,
化简得;
,
解得,,
甲乙两地的距离为公里.
答:甲乙两地的距离为公里.
设此人正常的速度为,行走的时间为,则根据如果每小时比原来的速度快公里,便可以早到分钟;如果每小时比原来的速度慢公里,便要迟到分钟列出关于、的方程组,求得、的值即可求解.
本题考查了二元一次方程组的应用,本题中列出关于、的方程组并且求、的值是解题的关键.
14.【答案】
【解析】
解:根据题意得,,
解得,
所以.
故答案为:.
根据方程组解的定义,把解代入方程组得到关于、的方程,然后求解得到、的值,再代入代数式进行计算即可得解.
本题考查了二元一次方程组的解,根据解的定义得到关于、的方程组并求出、的值是解题的关键.
15.【答案】
【解析】
解:设打折前商品每件元,商品每件元,根据题意,得:
,
解得:,
打折前买件商品和件商品需要元,
则打折后比打折前少花元,
故答案为:.
设打折前商品每件元,商品每件元,根据买件商品和件商品用了元;买件商品和件商品用了元.可列出方程组求得、商品的单件,继而可得打折前买件商品和件商品所需总费用,比较即可得答案.
考查了二元一次方程组的应用,解题关键是弄清题意,合适的等量关系,列出方程组,熟练运用代入消元法或加减消元法解方程组.
16.【答案】
【解析】
解:设花城团有人,穗城团有人,羊城团有人,
因为,,,
又,,.
根据公园门票优惠方法得方程组:,即;
,即;
,即.
三式相加得:,故,即三个团共有人.
由可知,穗城团与羊城团合起来有人,而应写成,即人只需有人买票,与题目中的不符.因此,穗城团、羊城团的人数加起来不可能是人而应是人,而,因为只有人才需要购买人的票,同样,由人,若再增加一人,变为人,则,省人的票,同样也是人买票.所以羊城团、花城团合起来可能是人,也可能是人.即可能是,也可能是综上所述,可得方程组: 或
由方程组可得:,故,
由方程组可得:,故,由于人数不可能为小数,
所以方程组不符合实际,应舍去,故三个团共有人.
故答案为:.
可设花城团有人,穗城团有人,羊城团有人,每人元,每人优惠人免票不足人的余数不优惠,实际上就是:元,可进人.可得方程组: 或,解方程组求解即可.
本题考查了三元一次方程组的应用,解题的关键是得出羊城团、花城团合起来可能是人,也可能是人,从而根据情况舍去不符合实际的.
17.【答案】
解:,
得:,即,
把代入得:,
则方程组的解为;
方程组整理得:,
得:,即,
把代入得:,
则方程组的解为.
【解析】
方程组利用加减消元法求出解即可;
方程组整理后,利用加减消元法求出解即可.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
18.【答案】
解:,
得:,
解得:,
把代入得:,
则方程组的解为;
方程组整理得:,
得:,
解得:,
把代入得:,
则方程组的解为.
【解析】
方程组利用加减消元法求出解即可;
方程组整理后,利用加减消元法求出解即可.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
19.【答案】
解:得:,
得:,
代入中,得:,
解得:.
则
【解析】
把看作已知数表示出方程组的解得到与,代入已知方程计算求出的值,即可求出原式的值.
此题考查了二元一次方程组的解,以及二元一次方程的解,熟练掌握运算法则是解本题的关键.
20.【答案】
解:解原方程组得,,
,
,解得,
.
【解析】
先用表示出方程组的解,再代入即可求出的值,代入代数式即可得出结论.
本题考查的是二元一次方程组的解,根据题意得出关于的一元一次方程是解答此题的关键.
21.【答案】
解:设辆甲种卡车一次可运土立方米,辆乙种卡车一次可运土立方米,
依题意,得:,
解得:,
.
答:辆甲种卡车与辆乙种卡车一次共可运土立方米.
【解析】
设辆甲种卡车一次可运土立方米,辆乙种卡车一次可运土立方米,根据“辆甲种卡车与辆乙种卡车一次共可运土立方米,辆甲种卡车与辆乙种卡车一次共可运土立方米”,即可得出关于,的二元一次方程组,解之即可得出,的值,再将其代入中即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
22.【答案】
解:设打折前商品的单价为元件,商品的单价为元件,
根据题意得:
解得:.
打折前,购买件商品和件商品一共要用元,
打折后,购买件商品和件商品一共要用元,
.
答:打了八折.
【解析】
设打折前商品的单价为元件,商品的单价为元件,根据“买件商品和件商品用了元;买件商品和件商品用了元”,即可得出关于、的二元一次方程组,解之即可得出、值,利用总价单价数量求出打折前所需费用,结合打折后少花的钱数即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
23.【答案】
解:设购买加工机械甲种台,乙种台,丙种台,由题意得:
,
解得:;
,
解得:舍去
,
解得:.
故两种方案:方案:甲种加工机械台,乙种加工机械台;
方案:购买甲种加工机械台,乙种加工机械台;
选择方案,理由:
商场销售一台甲种加工机械可获利元,销售一台乙种加工机械机可获利元,销售一台丙种加工机械可获利元,
方案:元,
方案:元,
故选择方案.
【解析】
通过理解题意可知本题存在两个等量关系,即“购进其中两种不同型号的加工机械共台”和“两种不同型号的加工机械共用去万元”,根据这两个等量关系可列出方程组.
根据中两种方案,分别求出利润即可.
此题主要考查了二元一次方程组的应用以及最佳方案问题,根据已知得出总钱数和总台数的方程是解题关键.
24.【答案】
解:由得:,即,
把代入得:,即,
把代入得:,
则方程组的解为;
由得:,即,
由得:,即,
整理得:,
;
,,
,即,
则原式.
【解析】
方程组中第二个方程变形后,将第一个方程代入求出的值,进而求出的值,得到方程组的解;
方程组第一个方程变形表示出,第二个方程变形后代入求出的值,进而求出的值;
利用完全平方公式及平方根定义求出的值,再由的值,即可求出所求式子的值.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
第2页,共2页
第1页,共1页
