数学高中苏教版必修一《幂函数》课件

课件23张PPT。2．4　幂函数学习目标
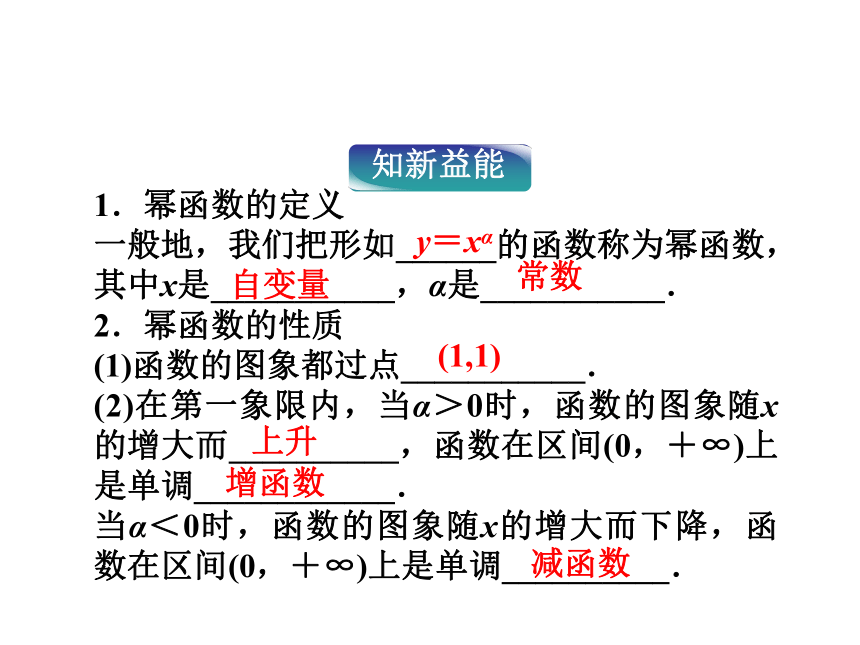
课堂互动讲练知能优化训练课前自主学案　幂函数2．4课前自主学案＜＜(－∞，0)∪(0，＋∞)[0，＋∞)1．幂函数的定义
一般地，我们把形如______的函数称为幂函数，其中x是___________，α是___________．
2．幂函数的性质
(1)函数的图象都过点___________．
(2)在第一象限内，当α＞0时，函数的图象随x的增大而__________，函数在区间(0，＋∞)上是单调____________．
当α＜0时，函数的图象随x的增大而下降，函数在区间(0，＋∞)上是单调__________．y＝xα自变量常数(1,1)上升增函数减函数1．函数y＝(2x)α是幂函数吗？
提示：不是，由幂函数定义可判断．
2．幂函数图象为什么不能过第四象限？
提示：若x＞0，不论幂函数y＝xα中α取何值，都不可能y＜0.课堂互动讲练幂函数的概念幂函数的结构特征是：函数右边为单项式，幂指数为常数，底数是自变量，前面系数为1.【思路点拨】　由已知f(x)＝(m2－m－5)·xm－1是幂函数，且当x＞0时是单调增函数，可先利用幂函数的定义求m的值，再利用单调性确定m的值．【解】　根据幂函数的定义得：
m2－m－5＝1，解得m＝3或m＝－2，
当m＝3时，f(x)＝x2在(0，＋∞)上是单调增函数；
当m＝－2时，f(x)＝x－3在(0，＋∞)上是单调减函数，不符合要求．
故m＝3.
【名师点评】　利用幂函数的定义，抓住其本质特征，这是判断一个函数是否为幂函数的重要依据和惟一标准，对本例来说，还要根据单调性验根，以免增根．
幂函数的图象特征【思路点拨】　利用幂函数的图象与指数的变化规律解决．【名师点评】　通过幂函数的图象比较指数的大小时，可作直线x＝m(m＞1)，依据直线x＝m(m＞1)与图象的交点的高低判断，其规律为：按交点自上而下，幂指数逐渐减小．幂值的大小问题比较两个幂值的大小首先要分清是指数相同，还是底数相同，若指数相同，则构造一个幂函数，利用幂函数的性质；若底数相同，则构造一个指数函数，利用指数函数的性质；若指数、底数皆不相同，则考虑构造一个中介值，用中介值法．【思路点拨】【名师点评】　比较大小时，利用相应函数的单调性是常用的方法．
自我挑战　比较下列各组中两个数的大小．
(4)任何两个幂函数图象最多有三个交点；
(5)α＝0时，图象是直线y＝1(除去点(0,1))．
2．(1)所有幂函数在(0，＋∞)上都有定义，并且图象都通过点(1,1)．
(2)α>0时，幂函数的图象通过原点，并且在区间[0，＋∞)上是增函数；α<0时，幂函数在(0，＋∞)上是减函数，图象不通过原点．(3)α>1时，y＝xα在第一象限的图象下凹；0<α<1时，y＝xα在第一象限的图象上凸；α<0时，y＝xα在第一象限的图象下凹．
(4)当α为奇数时，幂函数为奇函数；当α为偶数时，幂函数为偶函数．
本部分内容讲解结束Thank you!