数学高中苏教版必修一《映射的概念》课件
文档属性
| 名称 | 数学高中苏教版必修一《映射的概念》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 275.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-12 15:06:50 | ||
图片预览







文档简介
课件25张PPT。2.1.4 映射的概念学习目标
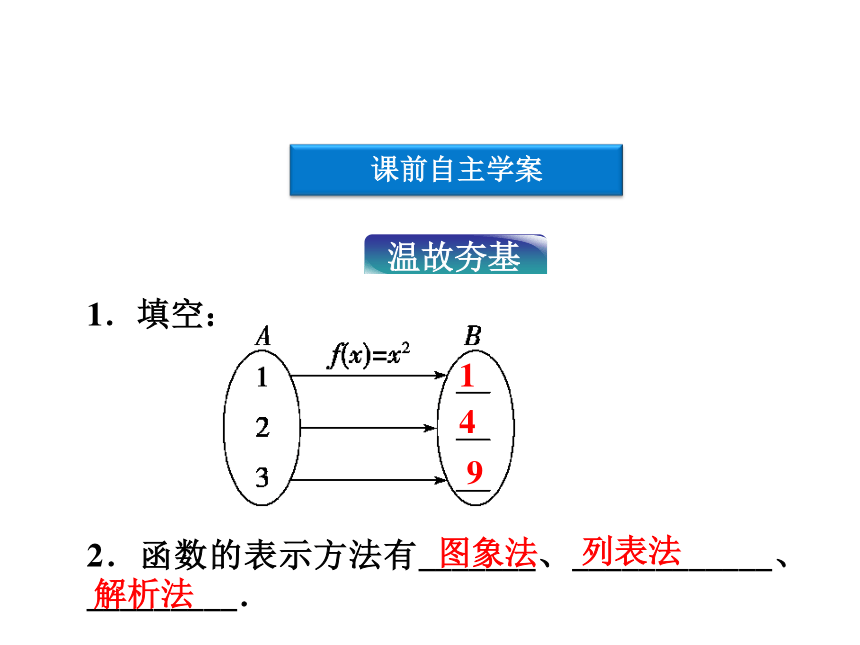
了解映射的概念,理解函数与映射的联系和区别. 课堂互动讲练知能优化训练课前自主学案映射的概念2.1.4课前自主学案1.填空:
2.函数的表示方法有_______、____________、_________.图象法列表法解析法149映射的定义
设A、B是两个非空集合,如果按照某种对应法则f,对于集合A中的______________,在集合B中都有______________与之对应,那么,这样的单值对应叫做集合A到集合B的映射,记为____________.每一个元素惟一的元素f:A→B在映射f:A→B中,B中的元素在集合A中都有元素与之对应吗?
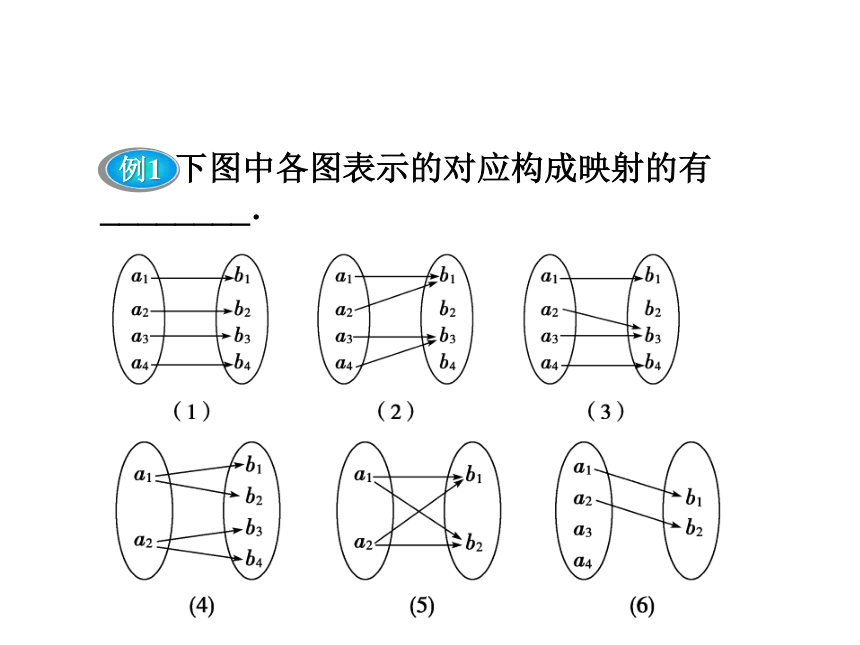
提示:不一定.集合B中可以有找不到与A中对应的元素,即“多出”一部分.课堂互动讲练映射概念的理解映射是一种特殊的对应,映射中的集合A、B可以是数集,也可以是点集或其他集合,这两个集合有先后次序,从A到B的映射与从B到A的映射是截然不同的. 下图中各图表示的对应构成映射的有________.【思路点拨】 所谓映射,是指多对一的对应或一对一的对应,且A中的元素无剩余,以此判断既准确,又迅速.
【解析】 (1)(2)(3)这三个图所表示的对应都符合映射的定义,即A中的每一个元素在对应法则下,B中都有惟一的元素与之对应.
对于(4)(5),A中的每一个元素在B中有2个元素与之对应,所以不是A到B的映射.
对于(6),A中的元素a3,a4在B中没有元素与之对应,所以不是A到B的映射.【答案】 (1)(2)(3)
【名师点评】 判断两个集合之间是否能构成映射,一般从映射的概念入手,若满足条件就构成映射,若不满足条件,要举出一个反例,即说明集合A中的某一元素,在B中无对应元素或有多个对应元素即可.互动探究1 下列各图中,建立了集合P中元素与集合M中元素的对应f,其中是映射的对应是哪些?为什么?解:图(1)(3)(4)都不是映射,因为(1)中集合P中的元素-3没有象;(3)中集合P中的元素2对应集合M中的元素3和4,不惟一,因此它也不是映射;(4)中集合P中的元素1对应集合M中的元素0.5和8,一对多,不是映射.(2)(5)是映射,符合映射的定义要求.
对于一个从集合A到集合B的映射来说,A中的每一个元素在B中必有惟一的元素与之对应,并且对A中不同的元素,在B中可以有相同的元素,但B中每一个元素却不一定都有与之对应的元素,如果有,也不一定只有一个.对应元素的求法【名师点评】 求映射中的对应元素,要准确地利用映射的关系,恰当地列出方程或方程组.求映射的个数映射的个数,设集合A中有m个元素,集合B中有n个元素,则从A到B的映射最多有nm个. (本题满分14分)已知A={a,b,c},B={-1,0,1},f是A到B的映射,且满足f(a)+f(b)+f(c)=0,求映射f:A→B的个数.
【思路点拨】 解答本题可先由对条件f(a)+f(b)+f(c)=0的分析入手,列表分情况表示,再由表得到满足的映射.
【规范解答】 由于f(a),f(b),f(c)∈{-1,0,1},故符合f(a)+f(b)+f(c)=0条件的f(a),f(b),f(c)的取值情况,如表所示
由上表可知,所求映射有7个.14分互动探究2 若将本例中的条件改为“f(a)·f(b)=f(c)”,则这样的映射有几个?
解:由于f(a),f(b),f(c)的取值属于集合
{-1,0,1},故f(a)·f(b)=f(c)时,f(a),f(b),f(c)取值的情况如表所示.
由表可知这样的映射有9个.1.映射的记号f:A→B,应明确映射是一种特殊的“对应”,它包括集合A、B以及A到B的对应法则f(A≠?,B≠?).
2.对于给出A到B的映射需要满足某些特殊要求,求映射的个数时,其关键是将映射具体化、形象化(如用列表法、图示法、数形结合法).3.要判断对应法则f:A→B是否是A到B的映射,必须注意:①集合A、B中的元素要明确;②根据映射定义判断A中每一个元素是否在集合B中都有惟一确定的元素与之对应;若进一步判断是否为一一映射,还需要进一步判断集合B中的每一个元素在A中是否有原象,集合A中的不同元素对应的象是否相同.本部分内容讲解结束Thank you!
了解映射的概念,理解函数与映射的联系和区别. 课堂互动讲练知能优化训练课前自主学案映射的概念2.1.4课前自主学案1.填空:
2.函数的表示方法有_______、____________、_________.图象法列表法解析法149映射的定义
设A、B是两个非空集合,如果按照某种对应法则f,对于集合A中的______________,在集合B中都有______________与之对应,那么,这样的单值对应叫做集合A到集合B的映射,记为____________.每一个元素惟一的元素f:A→B在映射f:A→B中,B中的元素在集合A中都有元素与之对应吗?
提示:不一定.集合B中可以有找不到与A中对应的元素,即“多出”一部分.课堂互动讲练映射概念的理解映射是一种特殊的对应,映射中的集合A、B可以是数集,也可以是点集或其他集合,这两个集合有先后次序,从A到B的映射与从B到A的映射是截然不同的. 下图中各图表示的对应构成映射的有________.【思路点拨】 所谓映射,是指多对一的对应或一对一的对应,且A中的元素无剩余,以此判断既准确,又迅速.
【解析】 (1)(2)(3)这三个图所表示的对应都符合映射的定义,即A中的每一个元素在对应法则下,B中都有惟一的元素与之对应.
对于(4)(5),A中的每一个元素在B中有2个元素与之对应,所以不是A到B的映射.
对于(6),A中的元素a3,a4在B中没有元素与之对应,所以不是A到B的映射.【答案】 (1)(2)(3)
【名师点评】 判断两个集合之间是否能构成映射,一般从映射的概念入手,若满足条件就构成映射,若不满足条件,要举出一个反例,即说明集合A中的某一元素,在B中无对应元素或有多个对应元素即可.互动探究1 下列各图中,建立了集合P中元素与集合M中元素的对应f,其中是映射的对应是哪些?为什么?解:图(1)(3)(4)都不是映射,因为(1)中集合P中的元素-3没有象;(3)中集合P中的元素2对应集合M中的元素3和4,不惟一,因此它也不是映射;(4)中集合P中的元素1对应集合M中的元素0.5和8,一对多,不是映射.(2)(5)是映射,符合映射的定义要求.
对于一个从集合A到集合B的映射来说,A中的每一个元素在B中必有惟一的元素与之对应,并且对A中不同的元素,在B中可以有相同的元素,但B中每一个元素却不一定都有与之对应的元素,如果有,也不一定只有一个.对应元素的求法【名师点评】 求映射中的对应元素,要准确地利用映射的关系,恰当地列出方程或方程组.求映射的个数映射的个数,设集合A中有m个元素,集合B中有n个元素,则从A到B的映射最多有nm个. (本题满分14分)已知A={a,b,c},B={-1,0,1},f是A到B的映射,且满足f(a)+f(b)+f(c)=0,求映射f:A→B的个数.
【思路点拨】 解答本题可先由对条件f(a)+f(b)+f(c)=0的分析入手,列表分情况表示,再由表得到满足的映射.
【规范解答】 由于f(a),f(b),f(c)∈{-1,0,1},故符合f(a)+f(b)+f(c)=0条件的f(a),f(b),f(c)的取值情况,如表所示
由上表可知,所求映射有7个.14分互动探究2 若将本例中的条件改为“f(a)·f(b)=f(c)”,则这样的映射有几个?
解:由于f(a),f(b),f(c)的取值属于集合
{-1,0,1},故f(a)·f(b)=f(c)时,f(a),f(b),f(c)取值的情况如表所示.
由表可知这样的映射有9个.1.映射的记号f:A→B,应明确映射是一种特殊的“对应”,它包括集合A、B以及A到B的对应法则f(A≠?,B≠?).
2.对于给出A到B的映射需要满足某些特殊要求,求映射的个数时,其关键是将映射具体化、形象化(如用列表法、图示法、数形结合法).3.要判断对应法则f:A→B是否是A到B的映射,必须注意:①集合A、B中的元素要明确;②根据映射定义判断A中每一个元素是否在集合B中都有惟一确定的元素与之对应;若进一步判断是否为一一映射,还需要进一步判断集合B中的每一个元素在A中是否有原象,集合A中的不同元素对应的象是否相同.本部分内容讲解结束Thank you!
